概括
结构模拟中最为人熟知的挑战之一在于实现精度和计算工作量之间的平衡。螺栓螺纹建模就是一个显著的例子,其中需要精确了解螺纹周围的应力分布。然而,计算成本往往迫使我们采取过度简化的方法以确保模拟的可行性。在本篇博文中,我们将探讨接触几何校正,这是一种有效协调这些相互竞争的需求的综合方法。
接触几何校正。
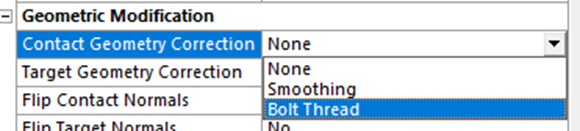
在 Ansys Mechanical Contacts 中,可以利用多种属性来增强接触性能。其中,“接触几何校正”提供两个选项:“平滑”适用于圆形和旋转几何,以及“螺栓螺纹”。
我们专门采用了“螺栓螺纹”选项,以便更全面地了解应力,而无需对实际螺纹的几何细节进行建模。简化模型能够基于内部执行的计算来近似螺栓的行为,以接近真实螺纹螺栓模型的精度进行建模。该技术适用于 2D 轴对称和 3D 模型,使用光滑的圆柱表面作为螺栓和螺母。它与各种类型兼容,包括无分离、无摩擦、粗糙和摩擦。必须明确定义不对称行为。
为了定义这一点,需要指定一些螺纹和旋转轴信息,其中大部分都是不言自明的。平均中径可以在标准螺栓尺寸表中找到:
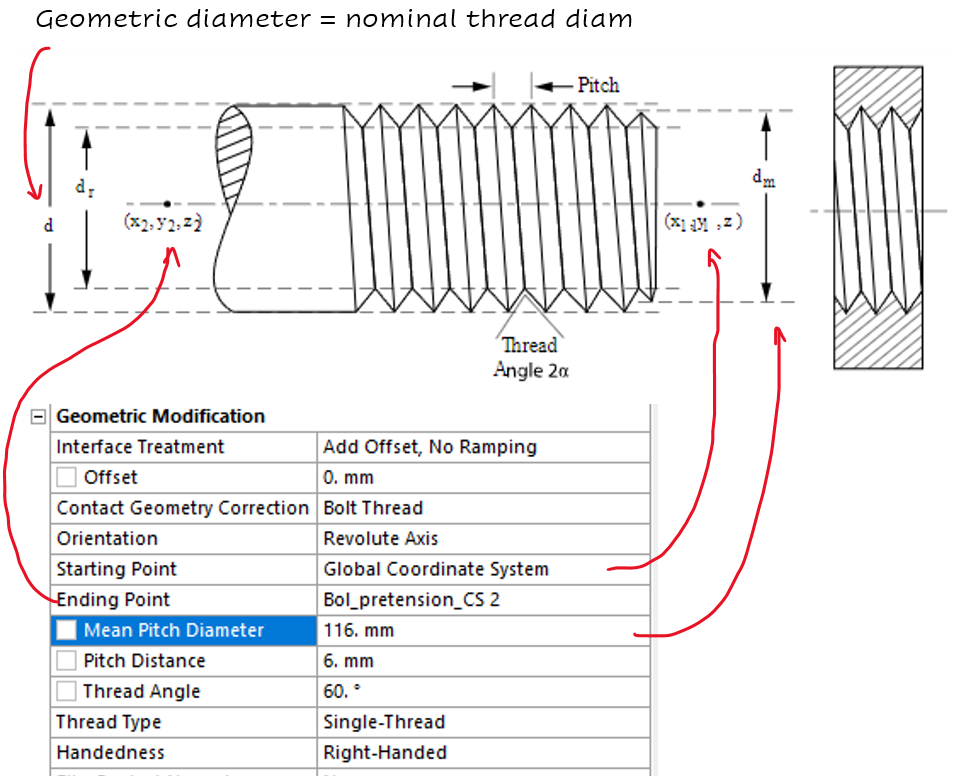
例子。
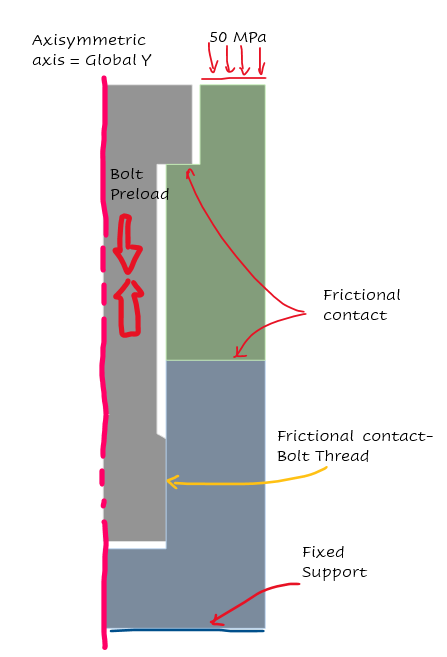
建立了一个 2D 轴对称模型来演示该技术的功能。该模型包括一个 120 毫米螺栓,在初始时间步长期间施加 2544690N 的轴向预紧力。有三个摩擦接触区:两个“经典接触”在两个板之间,另一个在螺栓头和上板之间,第三个简化接触用于模拟螺纹连接。对于所有接触,指定摩擦系数为 0.15。此外,在底线处采用固定支撑来约束模型。在随后的时间步长中,对上线施加 50 MPa 的压力以表示结构载荷并有助于缓解螺栓杆的张力。
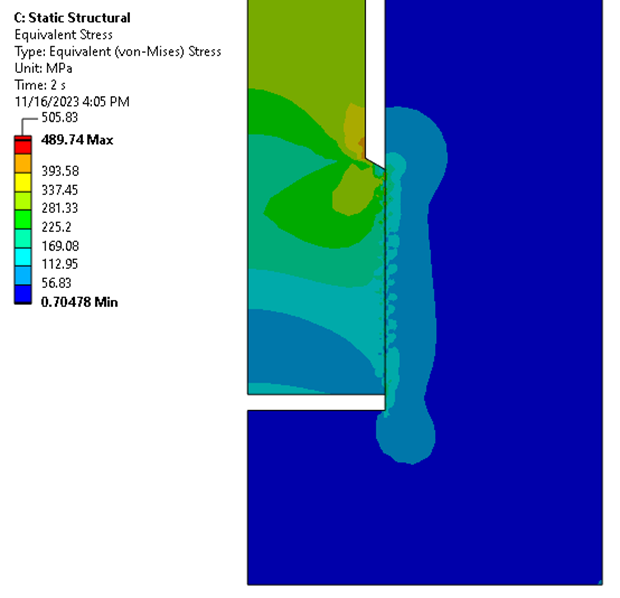
结果。
解决模型后,接触区中模拟螺纹几何形状的应力轮廓变得清晰可见。这让我们对该技术的有效性充满信心。
但这种方法有多好?确定其有效性的唯一方法是将这些结果与完全详细的几何模拟结果进行比较。在第二个模型中,所有设置都类似,结合螺纹几何并利用经典的摩擦接触。
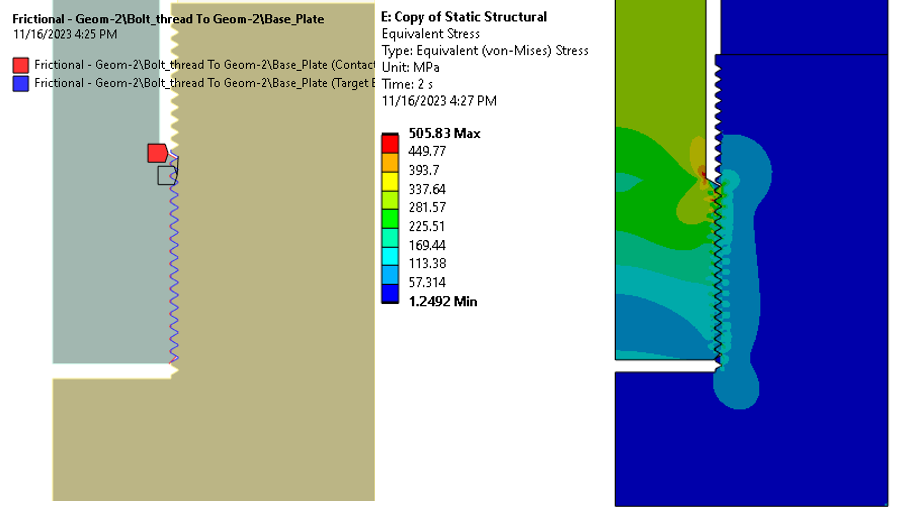
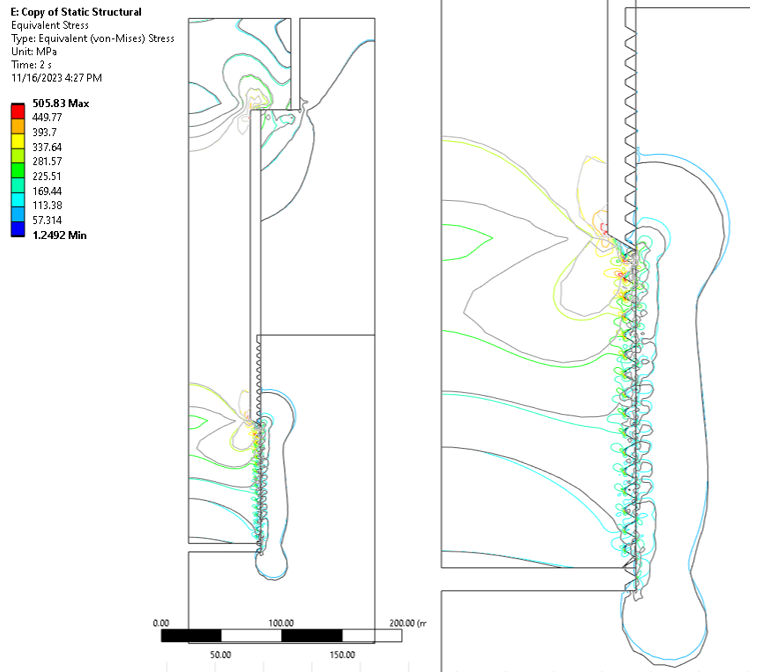
下图详细检查了应力轮廓。采用了等值线和等应力尺度,其中灰度线对应于简化的接触模型,而彩虹色线则表示来自完整详细模型的数据。相似性非常惊人。
比较网格计数和求解时间突出了该技术在资源消耗方面的优势:

建议。
在螺纹区域进行一些细化很重要。元素尺寸应小于螺距,以获得更准确的结果。
螺栓表面应为接触侧,且接触行为为不对称。
本例中定义为坐标系的轴点应位于适当的几何螺栓轴上。
结论。
当螺纹区附近的应力分布不是模拟的主要焦点时,这种技术尤其有吸引力。此外,它使用不太精细的网格和缩短的求解时间使其成为模拟规划中值得考虑的有利选择。






