伊吖学C笔记（1、二进制、补码、小数）

C语言编程基础(二进制、补码、小数)

一、计算机如何存储数据？

计算机要处理的信息是多种多样的，如数字、文字、符号、图形、音频、视频等，这些信息在人们的眼里是不同的。但对于计算机来说，它们在内存中都是一样的，都是以二进制的形式来表示。它是计算机处理数据的基础。

二、了解二进制产生。

1.硬件原理。

计算机硬件包括CPU、主板、GPU、内存、硬盘等，都是非常精密的部件。有的部件包含了上亿个电子元器件，它们很小，达到了纳米级别。这些元器件，实际上就是电路。给电路加的电压会有两种状态，要么是 0V，要么是 1.5V（‌常见工作电压有：0.7V~1.5V，3.3V，5V等）。1.5V 是通电，用1来表示，0V 是断电，用0来表示。所以，一个元器件有2种状态，即：不通电“0” 或者 通电“1”。也可理解为：通电，指示灯亮；不通电，灯不亮。

2.软件原理。

虽然一个元器件只能表示2个数值（通、断电），我们把很多元器件排列在一起，会得到很多0、1的组合，这样就可以表示很多数值了。例如，8个元器件站成一排，那么就有 2的8次方=256 种不同的组合，16个元器件有 2^16=65536 种不同的组合。我们给不同的组合赋予特定的含义，例如，用01000011来表示大写字母 C，上机操作如下：

依次定义3个字符变量，从地址观察可以看出，字符变量长度为一个字节。我们依次输出C的字符型和3种进制的值。二进制01000011在计算机内如果是字符型，表示大写字母C；如果是数字，则表示67。

我们再看看“C语言”这几个字在计算机里二进制是怎样的?

 

定义一个字符串——C语言，发现长度为5，不是3，说明一个汉字占2个字节，我们输出它的二进制如下：

那么“01000011 11010011 11101111 11010001 11010100”在计算机内部所表示的字符就是“C语言”。

3.计量单位。

一般情况下我们不一个一个的使用元器件，而是将8个元器件做成一排，看做一个单位。即使表示很小的数，例如 1，也需要8个，也就是 00000001。1个元器件称为1比特（Bit）或1位，8个元器件称为1字节（Byte），那么16个元器件就是2Byte，32个就是4Byte，以此类推：

8×1024个元器件就是1024Byte，简写为1KB；

8×1024×1024个元器件就是1024KB，简写为1MB；

8×1024×1024×1024个元器件就是1024MB，简写为1GB。

1TB = 1024GB。

三、二进制的定义与转换

1.定义。

二进制是一种基数为2的数制，仅使用0和1表示数值。每一位的权重是2的幂次方。二进制数10110.101表示：

2.不同进制数对比。

自然数“0”不能忽视，是一切数的开始。二进制表示每个位子存在两种可能：有（1）或没有（0）；十进制表示每个位子十种可能（0-9）。每个进制数的“10”表示的数值是不同的：分别为2、8、10、16。

3.二、八、十六进制之间的转换。

规律：3位二进制等于一位八进制，4位二进制等于一位十六进制。例：10110.10101，

二转八：以小数点为中心3位为一节（不足补0），

010，110.101，010=（八）26.52；

二转十六：以小数点为中心，4位一节，

0001，0110.1010，1000=（十六）16.a8；

二转大：分节压缩；大转二：扩充。八进制与十六进制之间转换：通过二进制过渡。

4.二进制与十进制转换。

二进制转十进制：根据定义直接计算求和。

十进制转二进制：

整数部分：除二取余（倒序）；小数部分：乘二取整（顺序）

可以发现，在十进制转二进制时，很多小数，通过乘二取整方法，得到的二进制无限长，C  语言浮点数总是有小误差，这真是二进制的不足之处。

四、原码, 反码, 补码的基础概念和计算方法

1、 原码。

原码是机器数的一种表示方法。在原码表示中，最高位表示符号位，“0”表示正数，“1”表示负数，其余位表示数值的绝对值。一个字节：10000000表示的不是0，而是-128，最小，01111111=127最大。C语言整数是4个字节，操作如下：

对于 8 位二进制数：

正数 5 的原码是 00000101 ，其中最高位 0 表示正数，后面 7 位 0000101 表示数值 5 。

负数 -5 的原码是 10000101 ，最高位 1 表示负数，后面 7 位 0000101 表示数值 5 。

原码的优点是直观易懂，与人的日常习惯比较接近。但在进行加减法运算时，需要单独处理符号位，比较复杂。比如计算 5 + (-5) ，用原码计算时，先分别写出 5 和 -5 的原码 00000101 和 10000101 ，然后进行加法运算，得到 10001010 ，其结果是 -10 ，这显然是错误的。这就体现出原码在进行运算时的不便，所以在计算机中，更多使用补码来进行运算。

2、反码。

反码也是机器数的一种表示方式。对于正数，其反码与原码相同；对于负数，其反码是在原码的基础上，符号位不变，其余各位取反。

对于 8 位二进制数：

正数 7 的原码和反码都是 00000111 。

负数 -7 的原码是 10000111 ，反码则是 11111000 。

反码的出现主要是为了在计算机运算中解决原码运算的一些问题，但它本身在运算中也存在一定的局限性。比如计算 -7 + 7 ，先写出 -7 的反码 11111000 ，7 的反码 00000111 ，相加得到 1 1111111 ，结果是 -127，并不是 0 。

所以，反码在实际计算机运算中使用较少，更多地是作为理解补码的一个过渡概念。

3、补码。

补码是计算机中一种重要的机器数表示方法。对于正数，其补码与原码相同；对于负数，其补码是在反码的基础上加 1 。

对于 8 位二进制数：

正数 4 的原码、反码和补码都是 00000100 。

负数 -4 ，原码是 10000100 ，反码是 11111011 ，补码+1则是 11111100 。

补码的优点在于可以将减法运算转换为加法运算，简化了计算机的运算逻辑。比如计算 5 - 3 ，可以转化为 5 + (-3) 。5 的补码是 00000101 ， -3 的补码是 11111101 ，两者相加得到 00000010 ，结果为 2 ，计算过程简单高效。

在计算机的存储和运算中，广泛使用补码来表示有符号数，极大地提高了运算的效率和准确性。操作验证如下：

int类型长度4个字节（从变量地址排列大小可以看出），二进制就是32位。上图中数字3表示为30个“0”和2个“1”，而-3则用补码表示。因为正数的补码还是自己，所以可以理解为：C语言整数用补码表示。

4.整数二进制加减。

先用手工计算看一下：

两个正数相加，如果相加的结果长度大于设定的位数，溢出了，出错。所以两个桶的水倒入一个桶中，要估算一个桶能否装的下，会不会溢出来？

减法变加法，补码来帮忙。

如何理解补码参与加减，结果还是正确的？

举例1：指针时钟，假如现在时间是5点，问：前3个小时是几点？这个简单5-3=2，2点。也可用笨办法：就是把时针往回拨3格，时针指向2点。

又问：前10小时是几点？这时5-10=-5，-5点是几点？不好说。用笨办法：把时针回拨10个格，指向7点。答案是7点。

这时再想一想，为什么要回拨10格？为什么不直接向前拨2个格？不也是7点，还少走弯路？

基于这种思路，把减法（-10）变加法（+2），结果一样。所以说：减法运算是可通过加法实现的，计算机中二进制减法，通过这种思路转换为加法实现。

我们再想想：为什么是+2？减多少、加多少之间有什么关联？10+2=12，这个12正好是时钟的一圈12个小时。所以说：12就是时钟的模（或理解为周期长度）。2就是10的补码，对于一个位数确定的数来说，本身+补码=模长。

时钟5-3：3的补码为9，5+9=14，14大于模长12，14-12=2，即为2点钟。

时钟5-10：10的补码为2，5+2=7，7点钟。用负数表示：7-12=-5。

在计算机里，存放一个数的长度是有规定的，比如1字节8位、4字节32位，这个长度就相当于时钟的12小时，就是模长。有了模长，才有了补码，才有了补码参与计算，减法变加法。

举例2：我们通过一个十进制补码运算，来加深理解。

我们规定一个两位数的十进制，在最高位增加一个符号位，用0表示正数，用9表示负数。比如：5表示为005，28表示028，-3表示为903，-56表示为956…等。

我们来看5-3是如果计算的：5-3=5+（-3）=005加903，903的反码：最高位符号位9不变，其他位取反，为996。这里的取反不象二进制要么0要么1，而是两个数加起来为个位数的最大值9，取反也就是用9去减该数。再+1取补，即996+1=997。两位十进制的模长为：99+1=100。

这时5+（-3）=005+997=1002，由于只限3位数，前面的1丢弃，结果变成002，正确。

我们再看3-5是如果计算的：3-5=3+（-5）=003加905，905的反码：994，补码：995。

这时3+（-5）=003+995=998，由于是负数，998再取补（取反+1）：结果902，正确。

五、c语言小数的二进制表示

问了Deepseek,回答如下：

基本了解：C语言小数，都是以指数表示，三部分：符号+指数+小数。二进制指数表示时，整数部分只可能为“1”，不象十进制还有2-9，这样更为简化1.m，小数部分只留m，还原时加1；符号部分与整数相同（0正1负）；指数部分还加个尾巴（偏置127，double型1023）。操作一下：

同样，从地址编号可以看出，float变量长度为4个字节。二进制表示跟上面讲的一样。变几个数看看：

如果错把float当然int输出，还真不好说，一哈正数，一哈0，一哈负数。到底是怎么回事呢？先看个有限小数：

整数输出为0，在一个printf里接连输出，会出现十六进制4028c000（十1076412416）。而通过指针输出该地址上的值为：41460000（十六）（十1095106560），这个值的二进制与定义是吻合的，即：符号1位+指数8位+小数23位。前面的0和一个数究竟是何道理呢？换个数试下：

这时变成了负数和一个正数。为了搞清楚这个问题，我们先看看double数是怎么搞起的。

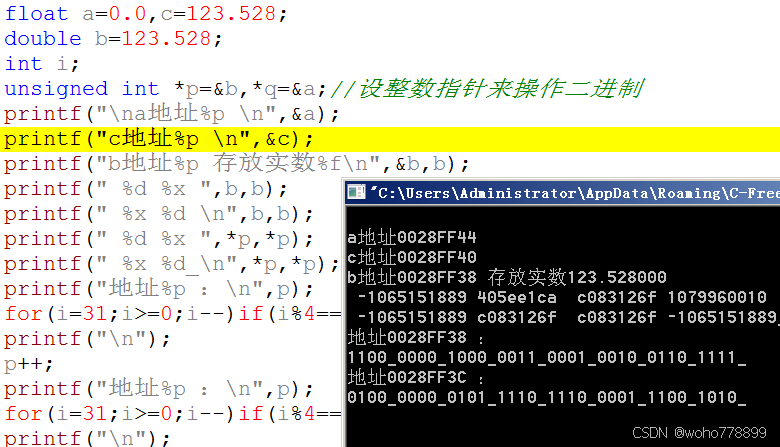
double数预设8个字节，从地址可以看出，没问题。分别输出它的十进制、十六进制、二进制，则完全吻合，只是高地址4字节放的小数表达的前32位(符号1+指数11+小数20），例中高地址0028FF3C存放的就是：

十六进制405ee1ca  = 十进制1079960010

=  二进制0100_0000_0101_1110_1110_0001_1100_1010

低地址部分0028FF38存放的数据c083126f,则是double数后32位的小数部分。

也就是说，double数据8字节存放规则是“中间一刀，首尾相连”，即：12345678-->56781234。所以，当我们把double数误当int数输出时，有时是正数，有时是0，有时是负数，这种结果就好理解了。

我们再回到前面一个图，float数123.528输出时，变量本身4个字节存放的是42f70e56（十六）1123487318（十），二进制为01000010 11110111 00001110 01010110，符合float定义格式。但用“%x”十六进制输出时，却是405ee1ca 和c0000000两节，这个405ee1ca刚好是小数123.528的double存放格式，只是后面一节只有一个c，两者加在一块为405ee1cac0000000。而123.528真正的double格式为405ee1cac083126f。

可以看出，float存放小数时，除了本身按32位存入4字节外，还在另外一处存放了一个double格式类型的备份，只是这个备份比真正的double精度小一点。当你格式输出（%d、%x）时，它取的是备份值。这也是网上所说的float提升，提升到double类型。

要想访问float变量的真实值，用整数指针即可。正float数不会出现负数，并且整数大小与原小数相当，不会出现交错乱序，这也就是，错把正小数当作整数排序，也会得到正确结果。