目录
一、需求分析
1.1 问题描述
1.2 数据需求
1.3 功能需求
1.4 开发环境
二、概要设计
2.1 抽象数据类型 ADT 的定义
2.2 系统的主要功能模块
2.3 功能模块联系图
三、详细设计
3.1 数据结构设计
3.2 主要算法
四、系统运行及结果分析
1. 用户界面
2. 程序运行样例
3. 程序结果分析
五、总结与思考
一、需求分析
1.1 问题描述
某工厂生产的产品需历经 3 道工序,为提升效率,需确定加工顺序,以实现生产 n 件产品的总时长最短。每件产品的各工序耗时各异。要求输入 n(n≥10),并递增 n 至少给出 3 组运行数据,对比程序运行时间。设计程序接收订单信息及工序时长,据此计算最短生产时间,即完成所有产品所需的最小时间。程序核心任务是依据输入优化工序安排,使总生产时间最小化。
1.2 数据需求
- 输入:订单信息:接收产品数量 n,代表工厂要生产的产品总数。
- 输入:工序时长信息:以二维矩阵或数组呈现,行对应产品,列对应工序,元素表示相应工序的时长。
1.3 功能需求
- 错误情况处理:输入订单及工序时长后,判断输入是否无效。若出现无效产品数量、负数工序时长等错误输入,进行错误提示或异常处理。
- 优化加工时长:运用分支限界法,根据输入的产品数量及各产品工序耗时,计算生产 n 件产品的最小总时长。
- 确定输出:依据输入,程序返回最小总时长,即完成 n 件产品所需的最短时间。
- 确定最优加工顺序:借助动态规划算法结果,确定使总时长最小的工序顺序。
1.4 开发环境
采用 Code::Blocks 作为开发环境,它是用于 C 和 C++ 等编程语言的集成开发环境(IDE),支持多种编译器,具备强大调试功能,可在开发中定位代码错误,还能将相关文件组织于项目中,便于代码管理、版本控制与共享,提高开发效率。
二、概要设计
2.1 抽象数据类型 ADT 的定义
ADT 结构体
-
- 数据对象:包含多种类型数据项,如变量、数组、指针等。
-
- 数据关系:数据项间存在相关性。
-
- 基本操作
-
-
- 创建:使用 typedef struct Node 创建新结构体对象。
-
-
-
- 访问:通过结构体对象和成员名访问成员。
-
-
-
- 赋值:将一个结构体对象赋值给当前对象。
-
-
-
- 修改:修改结构体中成员的值。
-
ADT info
-
- 数据对象:信息记录,含整型成员和数组成员。
-
- 数据关系:无特定关系描述。
-
- 基本操作:无特定操作描述。
ADT 线性表
-
- 数据对象:相同数据类型数据元素的集合。
-
- 数据关系:数据元素间有前驱后继关系。
-
- 基本操作
-
-
- 创建:构造空顺序表 L。
-
-
-
- 插入:向线性表 L 中插入元素 e。
-
-
-
- 删除:获取并删除线性表 L 的首个元素。
-
ADT 堆
-
- 数据对象:包含元素实际数据及在堆中的位置信息。
-
- 数据关系:对于非叶子节点 i,满足 data [i] >= data [2 * i + 1] 和 data [i] >= data [2 * i + 2](或 data [i] <= data [2 * i + 1] 和 data [i] <= data [2 * i + 2]);对于节点 i 和 j,当 i 是 j 的祖先节点时,data [j] <= data [i](或 data [j] >= data [i])。
-
- 初始条件:给定顺序表 L,起始位置 s 和结束位置 m。
-
- 操作结果:在给定范围内对顺序表 L 进行操作。
2.2 系统的主要功能模块
- inlIst 函数:初始化顺序表 L 为空。
- linsert 函数:向顺序表 L 插入元素。
- GetElem 函数:获取并删除顺序表 L 的首个元素。
- heaps 函数:实现堆排序中的堆调整操作。
- Creat 函数:构建大根堆。
- Sort 函数:对数组进行堆排序。
- Min1 函数:计算指定节点 k 与其他节点权重的最小值。
- Min2 函数:计算指定节点 k 与其他节点路径权重之和的最小值。
- fenzhi 函数:使用分支限界法求解最优路径问题。
- main 函数:程序入口,接收用户输入产品数量和加工时间,调用 fenzhi 函数求解最优路径。
- 异常处理模块:判断输入是否无效,对无效输入(如无效产品数量、负数工序时长)进行错误处理并给出提示。
2.3 功能模块联系图

三、详细设计
3.1 数据结构设计
- 结构体
typedef struct {int x;int Lw[100] = {0};int M[100] = {0};int g;} info;线性表
typedef struct {info data[MAXSIZE];int length;} Sqlist;堆
void heaps(Sqlist &L, int s, int m) { //堆的创建int j;info rc;memcpy(&rc, &L.data[s], sizeof(info));for (j = 2 * s; j <= m; j = j * 2) {if (j < m && L.data[j].x < L.data[j + 1].x)++j;if (rc.x >= L.data[j].x)break;memcpy(&L.data[s], &L.data[j], sizeof(info));s = j;}memcpy(&L.data[s], &rc, sizeof(info));}void Creat(Sqlist &L) { //对堆进行创建和调整int n, i;n = (L.length);for (i = n / 2; i > 0; --i)heaps(L, i, n);}void Sort(Sqlist &L) { //是对 L 中的数据进行排序。int i;info X;Creat(L);for (i = L.length; i > 1; --i) {memcpy(&X, &L.data[1], sizeof(info));memcpy(&L.data[1], &L.data[i], sizeof(info));memcpy(&L.data[i], &X, sizeof(info));heaps(L, 1, i - 1);}}3.2 主要算法
- Min1 函数
int Min1(int k, int n, int M[100]) {int j, min = 10000;for (j = 1; j <= n; j++) {if (M[j] == 0 && j != k && min > f[j][3])min = f[j][3];}if (min == 10000)min = f[k][3];return min;}该函数用于获取未被处理且工序时间最短的产品的工序时间,辅助求解最优路径。通过不断调用可在决策节点选择最优路径。
2. Min2 函数
int Min2(int k, int n, info p) {int j;int db, sumf = 0;for (j = 1; j <= n; j++) {if (p.M[j] == 0)sumf = sumf + f[j][2];}db = (max(Sum(1, p.g + 1, k, p), Sum(2, p.g, k, p)) + sumf + Min1(k, n, p.M));return db;}该函数用于计算当前节点的最小值,辅助求解最优路径。通过不断调用可在决策节点选择最优路径。
3. 分支限界法求解最优路径
void fenzhi(int n, Sqlist &L) {info p, pl, e;int down = 10000, up = 100000;int i, j, x, db, sumf = 0, min3 = 100000;for (i = 1; i <= n; i++) {for (j = 1; j <= n; j++) {sumf = sumf + f[j][2];}for (j = 1; j <= n; j++) {if (j != i && min3 > f[j][3])min3 = f[j][3];}db = f[i][1] + sumf + min3;if (down > db) {down = db;x = i;}}e.x = down;e.M[x] = 1;e.Lw[1] = x;e.g = 1;linsert(L, e);while (L.length != 0) {p = GetElem(L);if (p.Lw[n] != 0) {e = GetElem(L);printf("所需最短时间是:%d\n路径是: ", p.x);for (i = 1; i <= n; i++) {printf("%d ", p.Lw[i]);}} else {for (i = 1; i <= n; i++) {pl = p;if (p.M[i] == 0) {pl.Lw[p.g + 1] = i;pl.M[i] = 1;pl.g = p.g + 1;pl.x = Min2(i, n, p);if (pl.x < up) {linsert(L, pl);Sort(L);if (pl.g == n) {up = pl.x;deleted(down, up, L);}}}}}}}该函数实现分支限界法算法框架,通过生成新路径节点并选择最优路径,最终找到最优路径,输出最短时间和路径。
四、系统运行及结果分析
1. 用户界面

2. 程序运行样例


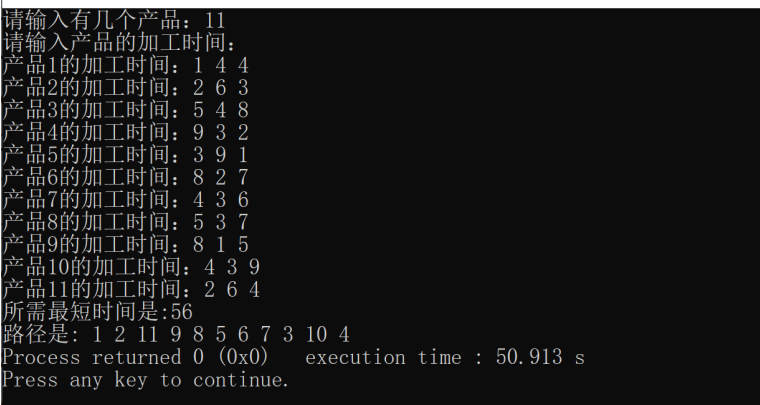
3. 程序结果分析
对比运行样例输出与手动计算结果,结果相似。同时记录不同 n 值下程序的运行时间,分析随着 n 增大,程序运行时间的变化趋势。若运行时间增长过快,可能需进一步优化算法或数据结构。
五、总结与思考
完成此作业过程中,深入学习了分支限界法及其应用。分支限界法是求解最优化问题的常用算法,通过搜索和剪枝高效寻找最优解。在此问题中,定义数据结构和函数,利用分支限界法搜索解空间,剪去不必要路径找到最优解。编写代码和运行程序过程中,深刻理解了分支限界法思想和实现。发现合理的排序和剪枝策略可大幅减少搜索空间、提高算法效率,且合理设计数据结构和算法能使代码更清晰易理解。此外,认识到编程中错误处理和输入验证的重要性,添加对无效输入的处理避免程序出错。总之,通过解决此问题,掌握了分支限界法应用,加深了对算法设计和错误处理的认识,为今后学习和工作奠定了基础。


、地图打印(webprinting)等服务)

——日期类和const成员函数)


