【java】实战-杨辉三角（ArrayList）

题目1描述：

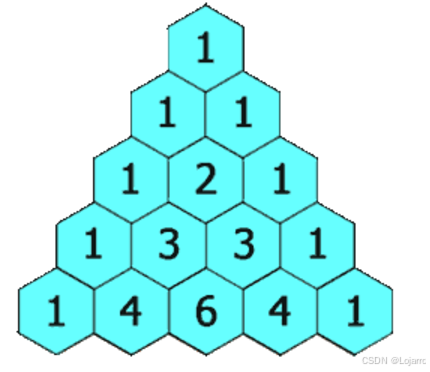
给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

分析：

n行

n维数组

第一行

1

1 1

1 2(arr[2][1]=arr[1][0]+arr[1][1]) 1

1 3(arr[3][1]=arr[2][0]+arr[2][1]) 3(arr[3][2]=arr2[2][1]+arr[2][2])  1

1 4(arr[4][1]=arr[3][0]+arr[3][1])  6(arr[4][2]=arr[3][1]+arr[3][2])  4(arr[4][3]=arr[3][2]+arr[3][3])   1

c[i][j]=c[i-1][j-1]+c[i-1][j]

class Solution {public List<List<Integer>> generate(int numRows) {List<List<Integer>> list=new ArrayList<>(numRows);list.add(List.of(1));for(int i=1;i<numRows;i++){List<Integer> row=new ArrayList<>(i+1);row.add(1);for(int j=1;j<i;j++){row.add(list.get(i-1).get(j-1)+list.get(i-1).get(j));}row.add(1);list.add(row);}return list;}
}

题目2描述

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

相似地：

class Solution {public List<Integer> getRow(int rowIndex) {List<List<Integer>> list=new ArrayList<>(rowIndex);list.add(List.of(1));for(int i=1;i<=rowIndex;i++){List<Integer> row=new ArrayList<>(i+1);row.add(1);for(int j=1;j<i;j++){row.add(list.get(i-1).get(j-1)+list.get(i-1).get(j));}row.add(1);list.add(row);}return list.get(rowIndex);}
}