从零开始学数据结构系列之第三章《二叉树链式结构及实现2》

---

前序/先序/根遍历

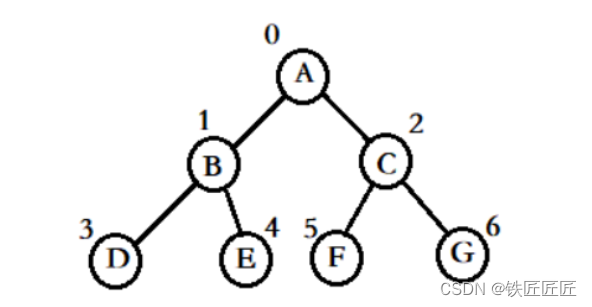
我们拿上图来举例




前序/先序/根遍历：

​   根遍历的原理就是，先遍历根，然后再遍历左子树，然后右子树

​   一句话来讲，就是 中 -> 左 -> 右

所以我们按如上顺序来算的话

  先遍历根树 A 之后根结束，开始遍历左子树

  于是到子树 B 发现B子树是D和E的“根”节点，于是继续向下寻找

继续到子树 D 之后就没有其他子树了，于是开始遍历右子树

  继续到子树 E 之后就没有其他子树了，因为已经全部遍历完了，开始回溯到B，再回溯到A，之后在开始遍历右子树

  继续到子树 C 发现C子树是F和G的“根”节点，于是继续向下寻找

  继续到子树 F 之后就没有其他子树了，于是开始遍历右子树

  继续到子树 G 之后就没有其他子树了，因为已经全部遍历完了，开始回溯到B，再回溯到A，结束遍历

所以根遍历的顺序就是

​   A->B->D->E->C->F->G

递归的方式：

void preOrder(TreeNode* T) 
{if(T == NULL)return;else{printf("%c->",T->data);preOrder(T->lchild);preOrder(T->rchild);}
}

非递归的方式，思想类似与栈的方式

验证代码

/*可以输入
ABD##E##CF##G##
来进行验证
*/#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define size 20typedef struct TreeNode 
{char data;struct TreeNode *lchild;struct TreeNode *rchild;
}TreeNode;typedef struct Node 
{TreeNode *data;struct Node *next;
}Node;void createTree(TreeNode** T,char* temp,int* index)
{char ch;ch = temp[*index];(*index)++;if( ch == '#') *T = NULL;else{*T =(TreeNode*)malloc(sizeof(TreeNode));(*T)->data = ch;createTree(&(*T)->lchild,temp,index);createTree(&(*T)->rchild,temp,index);		}
}
// 前序/先序/根遍历
void preOrder(TreeNode* T) 
{if(T==NULL)return;else{printf("%c->",T->data);preOrder(T->lchild);preOrder(T->rchild);}
}Node* initQueue() 
{Node* node = (Node*)malloc(sizeof(Node));node->data = NULL;node->next =NULL;return node;
}void enQueue(TreeNode* data, Node* list) 
{Node* node = (Node*)malloc(sizeof(Node));node->data = data;while(list->next)list=list->next;node->next = list->next;list->next=node;
}int isEmpty(Node* Q) 
{if(Q->next == NULL)return 1;elsereturn 0;
}Node* deQueue(Node* Q)
{if (isEmpty(Q)) return NULL;else {Node *node = Q->next;Q ->next = node->next;return node;}
}void levelTraverse(Node* Q, TreeNode* T) 
{enQueue(T, Q);while (!isEmpty(Q)) {Node* node = deQueue(Q);printf("%c->", node->data->data);if (node->data->lchild) {enQueue(node->data->lchild, Q);}if (node->data->rchild) {enQueue(node->data->rchild, Q);}}
}int main(int argc, char* argv[]) 
{TreeNode *T;int i=0;char *temp=NULL;Node* Q = initQueue();temp=(char*)malloc(sizeof(char) * (size+1));gets(temp);createTree(&T,temp,&i);preOrder(T);       printf("\n");levelTraverse(Q, T);printf("\n");return 0;
}

往期回顾

1.【第一章】《线性表与顺序表》
2.【第一章】《单链表》
3.【第一章】《单链表的介绍》
4.【第一章】《单链表的基本操作》
5.【第一章】《单链表循环》
6.【第一章】《双链表》
7.【第一章】《双链表循环》
8.【第二章】《栈》
9.【第二章】《队》
10.【第二章】《字符串暴力匹配》
11.【第二章】《字符串kmp匹配》
12.【第三章】《树的基础概念》
13.【第三章】《二叉树的存储结构》
14.【第三章】《二叉树链式结构及实现1》