隐马尔可夫模型(HMM)
时间序列模型: X = { x 1 , x 2 . … , x n } X=\{\mathbf{x}_1,\mathbf{x}_2.\dots,\mathbf{x}_n\} X={x1,x2.…,xn}
- n n n是序列长度
- x t ∈ R d \mathbf{x}_t\in\mathbb{R}^d xt∈Rd是 X X X在t时刻的观察数据
- 不满足独立假设、观测数据间具有很强的相关性。
**Q: 如何对序列数据表示、学习和推理? **
首先需要引入关于数据分布和时间轴依赖关系的概率模型,即如何表示 p ( x 1 , x 2 , … , x n ) p(\mathbf{x}_1,\mathbf{x}_2,\dots,\mathbf{x}_n) p(x1,x2,…,xn)
对 P ( X ) P(X) P(X)的假定
- 方法1具有极强的灵活性、通用性,但参数量大、计算复杂度高
- 方法2具有极差的灵活性、通用性,但参数量小、计算复杂度低
- 如何平衡灵活性和复杂度?
| 方法 | 联合分布 |
|---|---|
| 方法1:不对数据做任何独立性假设,直接对条件分布建模( x t \mathbf{x}_t xt和它的全部历史相关) | p ( x 1 , … , x n ) = p ( x 1 ) ∏ t = 2 n p ( x t ∣ x 1 , x 2 . … , x t − 1 ) p(\mathbf{x}_1,\dots,\mathbf{x}_n)=p(\mathbf{x_1})\prod^n_{t=2}p(\mathbf{x}_t\vert \mathbf{x}_1,\mathbf{x}_2.\dots,\mathbf{x}_{t-1} ) p(x1,…,xn)=p(x1)∏t=2np(xt∣x1,x2.…,xt−1) |
| 方法2:假设 { x 1 , x 2 . … , x n } \{\mathbf{x}_1,\mathbf{x}_2.\dots,\mathbf{x}_n\} {x1,x2.…,xn}独立,只对边缘分布建模 | p ( x 1 , … , x n ) = ∏ i = 1 n p ( x t ) p(\mathbf{x}_1,\dots,\mathbf{x}_n)=\prod^n_{i=1}p(\mathbf{x}_t) p(x1,…,xn)=∏i=1np(xt) |
| 方法3:(Markov性) x t \mathbf{x}_{t} xt只与 x t − 1 \mathbf{x}_{t-1} xt−1有关 p ( x t ∣ x 1 , … , x t − 1 ) = p ( x t ∣ x t − 1 ) p(\mathbf{x}_t\vert \mathbf{x}_1,\dots,\mathbf{x}_{t-1})=p(\mathbf{x}_t\vert \mathbf{x}_{t-1}) p(xt∣x1,…,xt−1)=p(xt∣xt−1) | p ( x 1 , … , x n ) = p ( x 1 ) ∏ t = 2 n p ( x t ∣ x t − 1 ) p(\mathbf{x}_1,\dots,\mathbf{x}_n)=p(\mathbf{x}_1)\prod^n_{t=2}p(\mathbf{x}_t\vert \mathbf{x}_{t-1}) p(x1,…,xn)=p(x1)∏t=2np(xt∣xt−1) |
HMM的表示
Markov链
静态、离散、一阶Markov链的联合分布:
p ( x 1 , … , x n ) = p ( x 1 ) ∏ t = 2 n p ( x t ∣ x t − 1 ) p(\mathbf{x}_1,\dots,\mathbf{x}_n)=p(\mathbf{x}_1)\prod^n_{t=2}p(\mathbf{x}_t\vert \mathbf{x}_{t-1}) p(x1,…,xn)=p(x1)t=2∏np(xt∣xt−1)
| 参数 | 说明 |
|---|---|
| 离散马氏链 | x t ∈ { 1 , 2 , … , K } , K \mathbf{x}_t\in\{1,2,\dots,K\},K xt∈{1,2,…,K},K为状态数 |
| 静态马氏链 | 转移概率 p ( x t ∣ x t − 1 ) p(\mathbf{x_t}\vert \mathbf{x_{t-1}}) p(xt∣xt−1)只与状态有关,与时间 t t t无关 |
| 初始状态分布 | p ( x 1 ) = π ∈ R K p(\mathbf{x}_1)=\pi\in\mathbb{R}^K p(x1)=π∈RK |
| 状态转移概率 | p ( x t ∣ x t − 1 ) = A ∈ R K × K p(\mathbf{x_t}\vert \mathbf{x_{t-1}})=A\in\mathbb{R}^{K\times K} p(xt∣xt−1)=A∈RK×K |

例子
- x t ∈ { 雨天 , 晴天 , 阴天 } , K = 3 \mathbf{x}_t \in \{雨天,晴天,阴天\}, K = 3 xt∈{雨天,晴天,阴天},K=3
- 初始状态分布: π = [ 0.1 , 0.6 , 0.3 ] \pi=[0.1, 0.6, 0.3] π=[0.1,0.6,0.3]
- 状态转移概率:
A = [ 0.1 0.4 0.5 0.1 0.6 0.3 0.2 0.4 0.4 ] A=\begin{bmatrix} 0.1 & 0.4 & 0.5 \\ 0.1 & 0.6 & 0.3 \\ 0.2 & 0.4 & 0.4 \end{bmatrix} A= 0.10.10.20.40.60.40.50.30.4
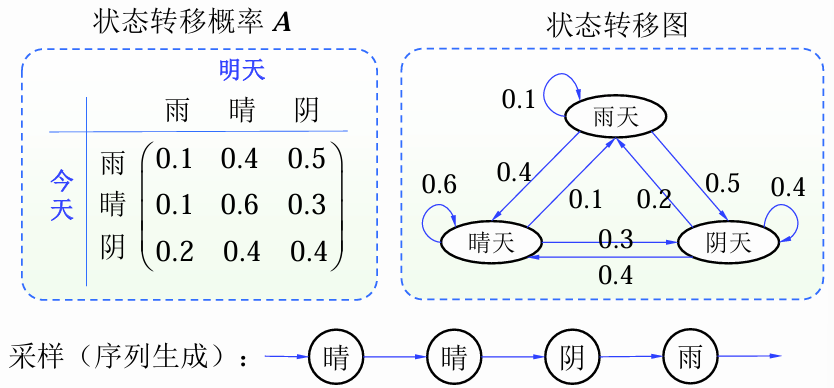
已知第 t t t天是雨天,第 t + 2 t + 2 t+2天是晴天的概率?
p ( x t ) = [ 1 , 0 , 0 ] T p ( x t + 1 ) = A T p ( x t ) = [ 0.1 , 0.4 , 0.5 ] T p ( x t + 2 ) = A T p ( x t + 1 ) = [ 0.15 , 0.48 , 0.37 ] T p(\mathbf{x}_t)=[1,0,0]^T\\ p(\mathbf{x}_{t + 1})=A^T p(\mathbf{x}_t)=[0.1, 0.4, 0.5]^T\\ p(\mathbf{x}_{t + 2})=A^T p(\mathbf{x}_{t + 1})=[0.15, 0.48, 0.37]^T p(xt)=[1,0,0]Tp(xt+1)=ATp(xt)=[0.1,0.4,0.5]Tp(xt+2)=ATp(xt+1)=[0.15,0.48,0.37]T
HMM简介
- HMM的基本思想
- 观测序列由一个不可见的马尔可夫链生成。
- HMM的随机变量可分为两组:
- 状态变量 { z 1 , z 2 , ⋯ , z n } \{z_1,z_2,\cdots,z_n\} {z1,z2,⋯,zn}:构成一阶、离散、静态马尔可夫链。用于描述系统内部的状态变化,通常是隐藏的,不可被观测的。其中, z t z_t zt表示第 t t t时刻系统的状态。
- 观测变量 { x 1 , x 2 , ⋯ , x n } \{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\} {x1,x2,⋯,xn}:其中, x t \mathbf{x}_t xt表示第 t t t时刻的观测变量,通过条件概率 p ( x t ∣ z t ) p(\mathbf{x}_t\vert z_t) p(xt∣zt)由状态变量 z t z_t zt生成;根据具体问题, x t \mathbf{x}_t xt可以是离散或连续,一维或多维。
- 主要用于时序数据建模,在CV、NLP、语音识别中有诸多应用。
HMM的图结构
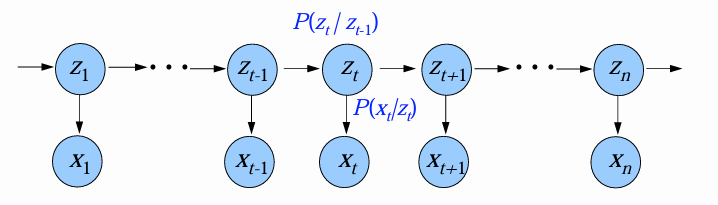
- 在图中,箭头表示依赖关系。
- t t t时刻的观测变量 x t \mathbf{x}_t xt的取值仅依赖于状态变量 z t z_t zt。当 z t z_t zt已知, x t \mathbf{x}_t xt与其它状态独立。
- t t t时刻的状态变量 z t z_t zt的取值仅依赖于 t − 1 t-1 t−1时刻的状态变量 z t − 1 z_{t-1} zt−1。当 z t − 1 z_{t-1} zt−1已知, z t z_t zt与其余 t − 2 t-2 t−2个状态独立。即 { z t } \{z_t\} {zt}构成马尔可夫链,系统下一刻的状态仅由当前状态决定,不依赖于以往任何状态。
HMM中的条件独立性:
p ( x 1 , ⋯ , x n ∣ z t ) = p ( x 1 , ⋯ , x t ∣ z t ) p ( x t + 1 , ⋯ , x n ∣ z t ) p ( x 1 , ⋯ , x n ∣ z t − 1 , z t ) = p ( x 1 , ⋯ , x t − 2 ∣ z t − 1 ) p ( x t − 1 ∣ z t − 1 ) p ( x t ∣ z t ) p ( x t + 1 , ⋯ , x n ∣ z t ) p ( x 1 , ⋯ , x t − 1 ∣ x t , z t ) = p ( x 1 , ⋯ , x t − 1 ∣ z t ) p ( x 1 , ⋯ , x t − 1 ∣ z t − 1 , z t ) = p ( x 1 , ⋯ , x t − 1 ∣ z t − 1 ) p ( x t + 1 , ⋯ , x n ∣ x t , z t ) = p ( x t + 1 , ⋯ , x n ∣ z t ) p ( x t + 1 , ⋯ , x n ∣ z t , z t + 1 ) = p ( x t + 1 , ⋯ , x n ∣ z t + 1 ) p(\mathbf{x}_1,\cdots,\mathbf{x}_n|z_t)=p(\mathbf{x}_1,\cdots,\mathbf{x}_t|z_t)p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_t)\\ p(\mathbf{x}_1,\cdots,\mathbf{x}_n|z_{t - 1},z_t)=p(\mathbf{x}_1,\cdots,\mathbf{x}_{t - 2}|z_{t - 1})p(\mathbf{x}_{t - 1}|z_{t - 1})p(\mathbf{x}_t|z_t)p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_t)\\\\ p(\mathbf{x}_1,\cdots,\mathbf{x}_{t - 1}|\mathbf{x}_t,z_t)=p(\mathbf{x}_1,\cdots,\mathbf{x}_{t - 1}|z_t)\\ p(\mathbf{x}_1,\cdots,\mathbf{x}_{t - 1}|z_{t - 1},z_t)=p(\mathbf{x}_1,\cdots,\mathbf{x}_{t - 1}|z_{t - 1})\\ p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|\mathbf{x}_t,z_t)=p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_t)\\ p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_t,z_{t + 1})=p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_{t + 1}) p(x1,⋯,xn∣zt)=p(x1,⋯,xt∣zt)p(xt+1,⋯,xn∣zt)p(x1,⋯,xn∣zt−1,zt)=p(x1,⋯,xt−2∣zt−1)p(xt−1∣zt−1)p(xt∣zt)p(xt+1,⋯,xn∣zt)p(x1,⋯,xt−1∣xt,zt)=p(x1,⋯,xt−1∣zt)p(x1,⋯,xt−1∣zt−1,zt)=p(x1,⋯,xt−1∣zt−1)p(xt+1,⋯,xn∣xt,zt)=p(xt+1,⋯,xn∣zt)p(xt+1,⋯,xn∣zt,zt+1)=p(xt+1,⋯,xn∣zt+1)
HMM联合概率分布:
p ( x 1 , ⋯ , x n , z 1 , ⋯ , z n ) = p ( z 1 ) ∏ t = 2 n p ( z t ∣ z t − 1 ) ∏ t = 1 n p ( x t ∣ z t ) p(\mathbf{x}_1,\cdots,\mathbf{x}_n,z_1,\cdots,z_n)=p(z_1)\prod_{t = 2}^n p(z_t|z_{t - 1})\prod_{t = 1}^n p(\mathbf{x}_t|z_t) p(x1,⋯,xn,z1,⋯,zn)=p(z1)t=2∏np(zt∣zt−1)t=1∏np(xt∣zt)
| 基本要素 | 对应公式 |
|---|---|
| 初始状态概率向量 π ∈ R K \pi \in R^K π∈RK | π k = P ( z 1 = k ) , 1 ≤ k ≤ K \pi_k = P(z_1 = k),\quad 1\leq k\leq K πk=P(z1=k),1≤k≤K |
| 状态转移概率矩阵 A ∈ R K × K A\in R^{K\times K} A∈RK×K | A i , j = P ( z t = j ∣ z t − 1 = i ) , 1 ≤ i , j ≤ K A_{i,j}=P(z_t = j\vert z_{t-1}=i),\quad 1\leq i,j\leq K Ai,j=P(zt=j∣zt−1=i),1≤i,j≤K |
| 发射概率矩阵 B ∈ R K × M B\in R^{K\times M} B∈RK×M | 离散: B i , j = P ( x t = j ∣ z t = i ) , 1 ≤ i ≤ K , 1 ≤ j ≤ M B_{i,j}=P(\mathbf{x}_t = j\vert z_t = i),\quad 1\leq i\leq K,1\leq j\leq M Bi,j=P(xt=j∣zt=i),1≤i≤K,1≤j≤M |
例子
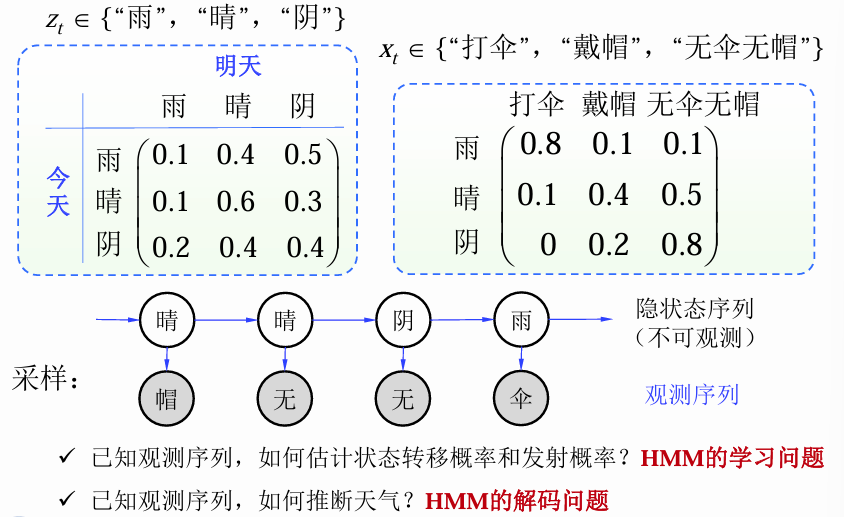
HMM的学习
三个基本问题
| 三个基本问题 | 简述 | 说明 |
|---|---|---|
| 给定模型 [ A , B , π ] [A,B,\pi] [A,B,π],如何有效地计算其产生观测序列 x = { x 1 , x 2 , ⋯ , x n } \mathbf{x}=\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\} x={x1,x2,⋯,xn}的概率 P ( x ∣ A , B , π ) P(\mathbf{x}\vert A,B,\pi) P(x∣A,B,π)? | 评估模型与观测数据的匹配程度。 | 许多任务需要根据以往的观测序列来预测当前时刻最有可能的观测值。 |
| 给定模型 [ A , B , π ] [A,B,\pi] [A,B,π]和观测序列 x = { x 1 , x 2 , ⋯ , x n } \mathbf{x}=\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\} x={x1,x2,⋯,xn},如何找到与此观测序列相匹配的状态序列 z = { z 1 , z 2 , ⋯ , z n } z=\{z_1,z_2,\cdots,z_n\} z={z1,z2,⋯,zn}? | 根据观测序列推断出隐藏的模型状态。(解码问题) | 在语言识别中,观测值为语音信号,隐藏状态为文字,目标就是观测信号推断最有可能的状态。 |
| 给定观测序列 x = { x 1 , x 2 , ⋯ , x n } \mathbf{x}=\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\} x={x1,x2,⋯,xn},如何调整模型参数 [ A , B , π ] [A,B,\pi] [A,B,π]使该序列出现的概率 P ( x ∣ A , B , π ) P(\mathbf{x}\vert A,B,\pi) P(x∣A,B,π)最大? | 如何模型使其能够最好地描述观测数据。(参数估计-学习问题) | 在大多数实际应用中,人工指定参数已变得不可行,需要根据训练样本学习最优模型。 |
参数学习的基本任务
通过拟合观测序列,确定HMM中的参数: θ = ( π , A , B ) \theta=(\pi,A,B) θ=(π,A,B)
EM算法步骤:
-
E Step: 对给定的 θ \theta θ,估计:
q ( z 1 , ⋯ , z n ) = p θ ( z 1 , ⋯ , z n ∣ x 1 , ⋯ , x n ) q(z_1,\cdots,z_n) = p_{\theta}(z_1,\cdots,z_n|\mathbf{x}_1,\cdots,\mathbf{x}_n) q(z1,⋯,zn)=pθ(z1,⋯,zn∣x1,⋯,xn) -
M Step: 用估计出的 q ( z 1 , ⋯ , z n ) q(z_1,\cdots,z_n) q(z1,⋯,zn),更新 θ \theta θ:
θ = arg max θ ∑ z q ( z 1 , ⋯ , z n ) ln p θ ( x 1 , ⋯ , x n , z 1 , ⋯ , z n ) \theta = \arg \max_{\theta} \sum_{z} q(z_1,\cdots,z_n) \ln p_{\theta}(\mathbf{x}_1,\cdots,\mathbf{x}_n,z_1,\cdots,z_n) θ=argθmaxz∑q(z1,⋯,zn)lnpθ(x1,⋯,xn,z1,⋯,zn) -
E步和M步迭代运行,直至收敛
M step: 更新 θ \theta θ
p θ ( x 1 , ⋯ , x n , z 1 , ⋯ , z n ) = p θ ( z 1 ) ∏ t = 2 n p θ ( z t ∣ z t − 1 ) ∏ t = 1 n p θ ( x t ∣ z t ) p_{\theta}(\mathbf{x}_1,\cdots,\mathbf{x}_n,z_1,\cdots,z_n)= p_{\theta}(z_1)\prod_{t = 2}^{n} p_{\theta}(z_t\vert z_{t-1})\prod_{t = 1}^{n} p_{\theta}(\mathbf{x}_t\vert z_t) pθ(x1,⋯,xn,z1,⋯,zn)=pθ(z1)∏t=2npθ(zt∣zt−1)∏t=1npθ(xt∣zt)
Q ( θ , θ o l d ) = ∑ z q ( z 1 , ⋯ , z n ) ln p θ ( x 1 , ⋯ , x n , z 1 , ⋯ , z n ) = ∑ z q ( z 1 , ⋯ , z n ) ( ln p θ ( z 1 ) + ∑ t = 2 n ln p θ ( z t ∣ z t − 1 ) + ∑ t = 1 n ln p θ ( x t ∣ z t ) ) = ∑ z 1 = 1 K q ( z 1 ) ln p θ ( z 1 ) + ∑ t = 2 n ∑ z t − 1 , z t = 1 K q ( z t − 1 , z t ) ln p θ ( z t ∣ z t − 1 ) + ∑ t = 1 n ∑ z t = 1 K q ( z t ) ln p θ ( x t ∣ z t ) = ∑ z 1 = 1 K q ( z 1 ) ln p θ ( π z 1 ) + ∑ t = 2 n ∑ z t − 1 , z t = 1 K q ( z t − 1 , z t ) ln A z t − 1 , z t + ∑ t = 1 n ∑ z t = 1 K q ( z t ) ln B z t , x t \begin{align*} Q(\theta,\theta^{old})&=\sum_{z} q(z_1,\cdots,z_n) \ln p_{\theta}(\mathbf{x}_1,\cdots,\mathbf{x}_n,z_1,\cdots,z_n)\\ &=\sum_{z} q(z_1,\cdots,z_n) (\ln p_{\theta}(z_1)+\sum_{t = 2}^{n} \ln p_{\theta}(z_t|z_{t - 1})+\sum_{t = 1}^{n} \ln p_{\theta}(\mathbf{x}_t|z_t))\\ &=\sum_{z_1=1}^K q(z_1) \ln p_{\theta}(z_1)+\sum_{t = 2}^{n} \sum_{z_{t - 1},z_t = 1}^{K} q(z_{t - 1},z_t) \ln p_{\theta}(z_t|z_{t - 1}) +\sum_{t = 1}^{n} \sum_{z_t = 1}^{K} q(z_t) \ln p_{\theta}(\mathbf{x}_t|z_t)\\ &=\sum_{z_1=1}^K q(z_1)\ln p_\theta(\pi_{z_1})+\sum_{t = 2}^{n} \sum_{z_{t - 1},z_t = 1}^{K} q(z_{t - 1},z_t) \ln A_{z_{t-1},z_t}+\sum_{t = 1}^{n} \sum_{z_t = 1}^{K} q(z_t) \ln B_{z_t,x_t} \end{align*} Q(θ,θold)=z∑q(z1,⋯,zn)lnpθ(x1,⋯,xn,z1,⋯,zn)=z∑q(z1,⋯,zn)(lnpθ(z1)+t=2∑nlnpθ(zt∣zt−1)+t=1∑nlnpθ(xt∣zt))=z1=1∑Kq(z1)lnpθ(z1)+t=2∑nzt−1,zt=1∑Kq(zt−1,zt)lnpθ(zt∣zt−1)+t=1∑nzt=1∑Kq(zt)lnpθ(xt∣zt)=z1=1∑Kq(z1)lnpθ(πz1)+t=2∑nzt−1,zt=1∑Kq(zt−1,zt)lnAzt−1,zt+t=1∑nzt=1∑Kq(zt)lnBzt,xt
用拉格朗日乘子法优化以下问题,可得:
| 参数 | 计算 | 约束 | 结果 |
|---|---|---|---|
| π \pi π | arg max π ∑ z 1 = 1 K q ( z 1 ) ln π z 1 \arg\max_{\pi} \sum_{z_1 = 1}^{K} q(z_1) \ln \pi_{z_1} argmaxπ∑z1=1Kq(z1)lnπz1 | ∑ k = 1 K π k = 1 \sum_{k = 1}^{K} \pi_k = 1 ∑k=1Kπk=1 | π k = q ( z 1 = k ) \pi_k = q(z_1 = k) πk=q(z1=k) |
| A A A | arg max A ∑ t = 2 n ∑ z t − 1 , z t = 1 K q ( z t − 1 , z t ) ln A z t − 1 , z t \arg\max_{A} \sum_{t = 2}^{n} \sum_{z_{t-1},z_t = 1}^{K} q(z_{t-1},z_t) \ln A_{z_{t-1},z_t} argmaxA∑t=2n∑zt−1,zt=1Kq(zt−1,zt)lnAzt−1,zt | ∀ i ∑ j = 1 K A i , j = 1 \forall i \sum_{j = 1}^{K} A_{i,j} = 1 ∀i∑j=1KAi,j=1 | A i , j = ∑ t = 2 n q ( z t − 1 = i , z t = j ) ∑ t = 2 n ∑ k = 1 K q ( z t − 1 = i , z t = k ) A_{i,j} = \frac{\sum_{t = 2}^{n} q(z_{t-1}=i,z_t = j)}{\sum_{t = 2}^{n} \sum_{k = 1}^{K} q(z_{t-1}=i,z_t = k)} Ai,j=∑t=2n∑k=1Kq(zt−1=i,zt=k)∑t=2nq(zt−1=i,zt=j) |
| B B B | arg max B ∑ t = 1 n ∑ z t = 1 K q ( z t ) ln B z t , x t \arg\max_{B} \sum_{t = 1}^{n} \sum_{z_t = 1}^{K} q(z_t) \ln B_{z_t,\mathbf{x}_t} argmaxB∑t=1n∑zt=1Kq(zt)lnBzt,xt | ∀ i ∑ j = 1 M B i , j = 1 \forall i \sum_{j = 1}^{M} B_{i,j} = 1 ∀i∑j=1MBi,j=1 | B i , j = ∑ t = 1 n 1 { x t = = j ^ } q ( z t = i ) ∑ t = 1 n q ( z t = i ) B_{i,j} = \frac{\sum_{t = 1}^{n} \mathbf{1}\{\mathbf{x}_t == \hat j\}q(z_t = i)}{\sum_{t = 1}^{n} q(z_t = i)} Bi,j=∑t=1nq(zt=i)∑t=1n1{xt==j^}q(zt=i) |
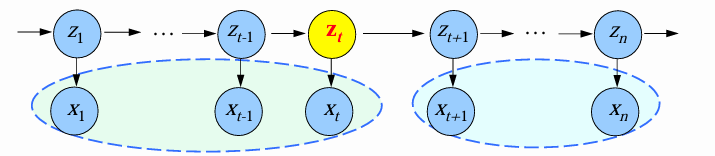
E Step: 对给定的 θ \theta θ,估计 q ( z 1 , ⋯ , z n ) = p θ ( z 1 , ⋯ , z n ∣ x 1 , ⋯ , x n ) q(z_1,\cdots,z_n)=p_{\theta}(z_1,\cdots,z_n\vert \mathbf{x}_1,\cdots,\mathbf{x}_n) q(z1,⋯,zn)=pθ(z1,⋯,zn∣x1,⋯,xn)
只需估计:
q ( z t ) = p θ ( z t ∣ x 1 , ⋯ , x n ) q ( z t − 1 , z t ) = p θ ( z t − 1 , z t ∣ x 1 , ⋯ , x n ) q(z_t) = p_{\theta}(z_t|\mathbf{x}_1,\cdots,\mathbf{x}_n)\\ q(z_{t - 1},z_t) = p_{\theta}(z_{t - 1},z_t|\mathbf{x}_1,\cdots,\mathbf{x}_n) q(zt)=pθ(zt∣x1,⋯,xn)q(zt−1,zt)=pθ(zt−1,zt∣x1,⋯,xn)
以下省略 θ \theta θ:
q ( z t ) = p ( x 1 , x 2 , ⋯ , x n , z t ) p ( x 1 , x 2 , ⋯ , x n ) = p ( x 1 , x 2 , ⋯ , x n ∣ z t ) p ( z t ) p ( x 1 , x 2 , ⋯ , x n ) = p ( x 1 , x 2 , ⋯ , x t ∣ z t ) p ( x t + 1 , ⋯ , x n ∣ z t ) p ( z t ) p ( x 1 , x 2 , ⋯ , x n ) = p ( x 1 , x 2 , ⋯ , x t , z t ) p ( x t + 1 , ⋯ , x n ∣ z t ) p ( x 1 , x 2 , ⋯ , x n ) q ( z t − 1 , z t ) = p ( x 1 , x 2 , ⋯ , x n , z t − 1 , z t ) p ( x 1 , x 2 , ⋯ , x n ) = p ( x 1 , x 2 , ⋯ , x n , z t ∣ z t − 1 ) p ( z t − 1 ) p ( x 1 , x 2 , ⋯ , x n ) = p ( x 1 , x 2 , ⋯ , x t − 1 ∣ z t − 1 ) p ( x t , ⋯ , x n , z t ∣ z t − 1 ) p ( z t − 1 ) p ( x 1 , x 2 , ⋯ , x n ) = p ( x 1 , x 2 , ⋯ , x t − 1 , z t − 1 ) p ( x t , ⋯ , x n , z t ∣ z t − 1 ) p ( x 1 , x 2 , ⋯ , x n ) \begin{align} q(z_t) &= \frac{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n,z_t)}{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)}=\frac{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n|z_t)p(z_t)}{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)}\\ &= \frac{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_t|z_t)p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_t)p(z_t)}{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)}\\ &=\frac{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_t,z_t)p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_t)}{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)}\\\\ q(z_{t - 1},z_t)&=\frac{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n,z_{t - 1},z_t)}{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)}\\ &=\frac{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n,z_t|z_{t - 1})p(z_{t - 1})}{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)}\\ &=\frac{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_{t - 1}|z_{t - 1})p(\mathbf{x}_t,\cdots,\mathbf{x}_n,z_t|z_{t - 1})p(z_{t - 1})}{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)}\\ & =\frac{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_{t - 1},z_{t - 1})p(\mathbf{x}_t,\cdots,\mathbf{x}_n,z_t|z_{t - 1})}{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)} \end{align} q(zt)q(zt−1,zt)=p(x1,x2,⋯,xn)p(x1,x2,⋯,xn,zt)=p(x1,x2,⋯,xn)p(x1,x2,⋯,xn∣zt)p(zt)=p(x1,x2,⋯,xn)p(x1,x2,⋯,xt∣zt)p(xt+1,⋯,xn∣zt)p(zt)=p(x1,x2,⋯,xn)p(x1,x2,⋯,xt,zt)p(xt+1,⋯,xn∣zt)=p(x1,x2,⋯,xn)p(x1,x2,⋯,xn,zt−1,zt)=p(x1,x2,⋯,xn)p(x1,x2,⋯,xn,zt∣zt−1)p(zt−1)=p(x1,x2,⋯,xn)p(x1,x2,⋯,xt−1∣zt−1)p(xt,⋯,xn,zt∣zt−1)p(zt−1)=p(x1,x2,⋯,xn)p(x1,x2,⋯,xt−1,zt−1)p(xt,⋯,xn,zt∣zt−1)
前向-后向算法(forward-backward algorithm)
q ( z t ) = p ( x 1 , x 2 , ⋯ , x t , z t ) p ( x t + 1 , ⋯ , x n ∣ z t ) p ( x 1 , x 2 , ⋯ , x n ) q ( z t − 1 , z t ) = p ( x 1 , x 2 , ⋯ , x t − 1 , z t − 1 ) p ( x t , ⋯ , x n , z t ∣ z t − 1 ) p ( x t + 1 , ⋯ , x n ∣ z t ) p ( x 1 , x 2 , ⋯ , x n ) q(z_t) = \frac{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_t,z_t)p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_t)}{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)}\\ q(z_{t - 1},z_t) = \frac{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_{t - 1},z_{t - 1})p(\mathbf{x}_t,\cdots,\mathbf{x}_n,z_t|z_{t - 1})p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_t)}{p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)} q(zt)=p(x1,x2,⋯,xn)p(x1,x2,⋯,xt,zt)p(xt+1,⋯,xn∣zt)q(zt−1,zt)=p(x1,x2,⋯,xn)p(x1,x2,⋯,xt−1,zt−1)p(xt,⋯,xn,zt∣zt−1)p(xt+1,⋯,xn∣zt)
-
前向概率: α t ( z t ) = p ( x 1 , ⋯ , x t , z t ) \alpha_t(z_t) = p(\mathbf{x}_1,\cdots,\mathbf{x}_t,z_t) αt(zt)=p(x1,⋯,xt,zt)
-
后向概率: β t ( z t ) = p ( x t + 1 , ⋯ , x n ∣ z t ) \beta_t(z_t) = p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n\vert z_t) βt(zt)=p(xt+1,⋯,xn∣zt)
-
观测概率: p ( x 1 , x 2 , ⋯ , x n ) = ∑ k = 1 K α n ( z n ) p(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)=\sum_{k = 1}^{K} \alpha_n(z_n) p(x1,x2,⋯,xn)=∑k=1Kαn(zn)
q ( z t ) = α t ( z t ) β t ( z t ) ∑ z n = 1 K α n ( z n ) , q ( z t − 1 , z t ) = α t − 1 ( z t − 1 ) p ( z t ∣ z t − 1 ) p ( x t ∣ z t ) β t ( z t ) ∑ z n = 1 K α n ( z n ) q(z_t) = \frac{\alpha_t(z_t)\beta_t(z_t)}{\sum_{z_n = 1}^{K} \alpha_n(z_n)},\quad q(z_{t - 1},z_t) = \frac{\alpha_{t - 1}(z_{t - 1})p(z_t|z_{t - 1})p(\mathbf{x}_t|z_t)\beta_t(z_t)}{\sum_{z_n = 1}^{K} \alpha_n(z_n)} q(zt)=∑zn=1Kαn(zn)αt(zt)βt(zt),q(zt−1,zt)=∑zn=1Kαn(zn)αt−1(zt−1)p(zt∣zt−1)p(xt∣zt)βt(zt)
从前向后计算, t = 1 , ⋯ , n t = 1,\cdots,n t=1,⋯,n
α t ( z t ) = p ( x 1 , ⋯ , x t , z t ) = ∑ z t − 1 p ( x 1 , ⋯ , x t , z t − 1 , z t ) = ∑ z t − 1 p ( x 1 , ⋯ , x t , z t ∣ z t − 1 ) p ( z t − 1 ) = ∑ z t − 1 p ( x 1 , ⋯ , x t − 1 ∣ z t − 1 ) p ( x t , z t ∣ z t − 1 ) p ( z t − 1 ) = ∑ z t − 1 p ( x 1 , ⋯ , x t − 1 , z t − 1 ) p ( x t , z t ∣ z t − 1 ) = ∑ z t − 1 α t − 1 ( z t − 1 ) p ( z t ∣ z t − 1 ) p ( x t ∣ z t ) = p ( x t ∣ z t ) ∑ z t − 1 α t − 1 ( z t − 1 ) p ( z t ∣ z t − 1 ) \begin{align*} \alpha_t(z_t)&=p(\mathbf{x}_1,\cdots,\mathbf{x}_t,z_t)=\sum_{z_{t - 1}} p(\mathbf{x}_1,\cdots,\mathbf{x}_t,z_{t - 1},z_t)\\ &=\sum_{z_{t - 1}} p(\mathbf{x}_1,\cdots,\mathbf{x}_t,z_t|z_{t - 1})p(z_{t - 1})\\ &=\sum_{z_{t - 1}} p(\mathbf{x}_1,\cdots,\mathbf{x}_{t - 1}|z_{t - 1})p(\mathbf{x}_t,z_t|z_{t - 1})p(z_{t - 1})\\ &=\sum_{z_{t - 1}} p(\mathbf{x}_1,\cdots,\mathbf{x}_{t - 1},z_{t - 1})p(\mathbf{x}_t,z_t|z_{t - 1})\\ &=\sum_{z_{t - 1}} \alpha_{t - 1}(z_{t - 1})p(z_t|z_{t - 1})p(\mathbf{x}_t|z_t)\\ &=p(\mathbf{x}_t|z_t)\sum_{z_{t - 1}} \alpha_{t - 1}(z_{t - 1})p(z_t|z_{t - 1}) \end{align*} αt(zt)=p(x1,⋯,xt,zt)=zt−1∑p(x1,⋯,xt,zt−1,zt)=zt−1∑p(x1,⋯,xt,zt∣zt−1)p(zt−1)=zt−1∑p(x1,⋯,xt−1∣zt−1)p(xt,zt∣zt−1)p(zt−1)=zt−1∑p(x1,⋯,xt−1,zt−1)p(xt,zt∣zt−1)=zt−1∑αt−1(zt−1)p(zt∣zt−1)p(xt∣zt)=p(xt∣zt)zt−1∑αt−1(zt−1)p(zt∣zt−1)
从后向前计算, t = n , n − 1 , ⋯ , 1 t = n,n-1,\cdots,1 t=n,n−1,⋯,1
β t ( z t ) = p ( x t + 1 , ⋯ , x n ∣ z t ) = ∑ z t + 1 p ( x t + 1 , ⋯ , x n , z t + 1 ∣ z t ) = ∑ z t + 1 p ( x t + 1 , ⋯ , x n ∣ z t , z t + 1 ) p ( z t + 1 ∣ z t ) = ∑ z t + 1 p ( x t + 1 , ⋯ , x n ∣ z t + 1 ) p ( z t + 1 ∣ z t ) = ∑ z t + 1 p ( x t + 2 , ⋯ , x n ∣ z t + 1 ) p ( x t + 1 ∣ z t + 1 ) p ( z t + 1 ∣ z t ) = ∑ z t + 1 β t + 1 ( z t + 1 ) p ( x t + 1 ∣ z t + 1 ) p ( z t + 1 ∣ z t ) \begin{align*} \beta_t(z_t)&=p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_t)=\sum_{z_{t + 1}} p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n,z_{t + 1}|z_t)\\ &=\sum_{z_{t + 1}} p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_t,z_{t + 1})p(z_{t + 1}|z_t)\\ &=\sum_{z_{t + 1}} p(\mathbf{x}_{t + 1},\cdots,\mathbf{x}_n|z_{t + 1})p(z_{t + 1}|z_t)\\ &=\sum_{z_{t + 1}} p(\mathbf{x}_{t + 2},\cdots,\mathbf{x}_n|z_{t + 1})p(\mathbf{x}_{t + 1}|z_{t + 1})p(z_{t + 1}|z_t)\\ &=\sum_{z_{t + 1}} \beta_{t + 1}(z_{t + 1})p(\mathbf{x}_{t + 1}|z_{t + 1})p(z_{t + 1}|z_t) \end{align*} βt(zt)=p(xt+1,⋯,xn∣zt)=zt+1∑p(xt+1,⋯,xn,zt+1∣zt)=zt+1∑p(xt+1,⋯,xn∣zt,zt+1)p(zt+1∣zt)=zt+1∑p(xt+1,⋯,xn∣zt+1)p(zt+1∣zt)=zt+1∑p(xt+2,⋯,xn∣zt+1)p(xt+1∣zt+1)p(zt+1∣zt)=zt+1∑βt+1(zt+1)p(xt+1∣zt+1)p(zt+1∣zt)
HMM的解码
-
在实际问题中,状态变量通常有明确的含义。如语音识别中, z t z_t zt表示语音信号 x t \mathbf{x}_t xt对应的文本。因此,经常需要根据观测序列推断状态序列。
-
对给定的HMM模型 θ = ( π , A , B ) \theta = (\pi, A, B) θ=(π,A,B)和观测序列 { x 1 , x 2 , ⋯ , x n } \{\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n\} {x1,x2,⋯,xn},求解:
z ∗ = arg max z p θ ( z 1 , ⋯ , z n ∣ x 1 , ⋯ , x n ) z^* = \arg\max_{z} p_{\theta}(z_1, \cdots, z_n | \mathbf{x}_1, \cdots, \mathbf{x}_n) z∗=argzmaxpθ(z1,⋯,zn∣x1,⋯,xn)
z ∗ z^* z∗是最大后验概率对应的状态序列,也称为最优状态路径。 -
这对应分类问题中的最大后验概率决策, z t z_t zt对应 x t \mathbf{x}_t xt的类别。
-
与分类中对 x t \mathbf{x}_t xt独立解码不同,HMM需要联合解码。
状态路径: z 1 , ⋯ , z n z_1, \cdots, z_n z1,⋯,zn
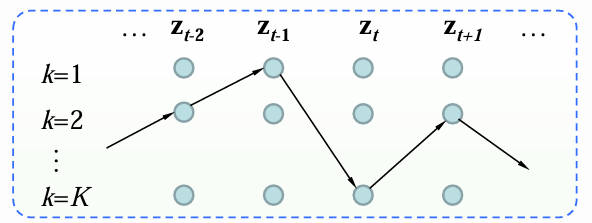
- 对于给定的HMM模型和观测序列 { x 1 , x 2 , ⋯ , x n } \{\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n\} {x1,x2,⋯,xn},不同状态路径对应不同的后验概率: p θ ( z 1 , ⋯ , n ∣ x 1 , ⋯ , x n ) p_{\theta}(z_1, \cdots, _n \vert \mathbf{x}_1, \cdots, \mathbf{x}_n) pθ(z1,⋯,n∣x1,⋯,xn)。
- 共有 K n K^n Kn条可能的状态路径,对应 K n K^n Kn个概率值。
- 直接计算这些概率,然后选出 z ∗ z^* z∗的复杂度为 O ( K n ) O(K^n) O(Kn)。
HMM的解码算法:维特比算法(Viterbi, 1967)
-
最优子问题:寻找以状态 z t z_t zt结束的前 t t t步最优状态路径
w t ( z t ) ≡ max ln p θ ( x 1 , ⋯ , x t , z 1 , ⋯ , z t − 1 , z t ) ∈ R K z ∗ = arg max z p θ ( z 1 , ⋯ , z n ∣ x 1 , ⋯ , x n ) ⇔ arg max z p θ ( z 1 , ⋯ , z n , x 1 , ⋯ , x n ) w_t(z_t) \equiv \max\ln p_{\theta}(\mathbf{x}_1, \cdots, \mathbf{x}_t, z_1, \cdots, z_{t - 1}, z_t) \in R^K\\ z^* = \arg\max_{z} p_{\theta}(z_1, \cdots, z_n | \mathbf{x}_1, \cdots, \mathbf{x}_n) \Leftrightarrow \arg\max_{z} p_{\theta}(z_1, \cdots, z_n, \mathbf{x}_1, \cdots, \mathbf{x}_n) wt(zt)≡maxlnpθ(x1,⋯,xt,z1,⋯,zt−1,zt)∈RKz∗=argzmaxpθ(z1,⋯,zn∣x1,⋯,xn)⇔argzmaxpθ(z1,⋯,zn,x1,⋯,xn) -
动态规划算法
-
For z 1 = 1 , ⋯ , K z_1 = 1, \cdots, K z1=1,⋯,K: w 1 ( z 1 ) = ln p ( z 1 ) + ln p ( x 1 ∣ z 1 ) w_1(z_1) = \ln p(z_1) + \ln p(\mathbf{x}_1 \vert z_1) w1(z1)=lnp(z1)+lnp(x1∣z1)
-
For t = 2 , ⋯ , n t = 2, \cdots, n t=2,⋯,n:
- For z t = 1 , ⋯ , K z_t = 1, \cdots, K zt=1,⋯,K:
w t ( z t ) = ln p ( x t ∣ z t ) + max z t − 1 ∈ { 1 , ⋯ , K } { w t − 1 ( z t − 1 ) + ln p ( z t ∣ z t − 1 ) } w_t(z_t) = \ln p(\mathbf{x}_t | z_t) + \max_{z_{t - 1} \in \{1, \cdots, K\}} \{w_{t - 1}(z_{t - 1}) + \ln p(z_t | z_{t - 1})\} wt(zt)=lnp(xt∣zt)+zt−1∈{1,⋯,K}max{wt−1(zt−1)+lnp(zt∣zt−1)}
- For z t = 1 , ⋯ , K z_t = 1, \cdots, K zt=1,⋯,K:
-
-
计算复杂度: O ( n K 2 ) O(nK^2) O(nK2)





