学习率在梯度法中的影响以及调整策略

2025/8/13 0:00:45 来源：https://blog.csdn.net/lzm12278828/article/details/144870842 浏览: 次关键词：学习率在梯度法中的影响以及调整策略

一、关于梯度法的运算过程

1.损失函数

假设我们有一个简单的线性回归模型的预测函数 $h_{\theta }(x)$ ：

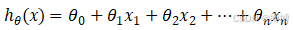
其中 $\theta$ 是一个包含多个参数的向量，即 $\theta =[\theta _{1},\theta _{2},...,\theta _{n}]$ 。我们的目标是计算损失函数关于每个参数 $\theta _{i}$ 的偏导数 $\frac{\partial J}{\partial \theta _{i}}$ ，用它来衡量模型预测值与实际值之间的差异或误差。对于简单线性回归来说，最简化结构可表示为：

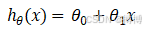
其损失函数 $J(\theta )$ 我们采用均方误差（MSE），它是预测值与目标值之间差值平方和的均值，而且函数曲线光滑、连续且处处可导；对较大的误差给予较大的惩罚，对较小的误差给予较小的惩罚；对离群点敏感，因为平方运算会放大较大误差的影响。则损失函数如下：

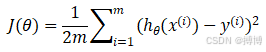
$\theta$ 是我们要优化的参数，对于本例它包含 $\theta _{0}$ 和 $\theta _{1}$ 。 $x^{(i)}$ 和 $y^{(i)}$ 分别是第 $i$ 个样本的特征和标签， $m$ 是样本数量。我们需要收集有数据集 ${(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})}$ 来计算损失并确定参数 $\theta _{0}$ 和 $\theta _{1}$ 的值。

学习率在梯度法中的影响以及调整策略

一、关于梯度法的运算过程

1.损失函数

相关资讯

热文排行

最新新闻

推荐新闻

热搜词