二叉树是编程中经常使用的一种数据结构,今天我们来学习一下二叉树。
二叉树的介绍:
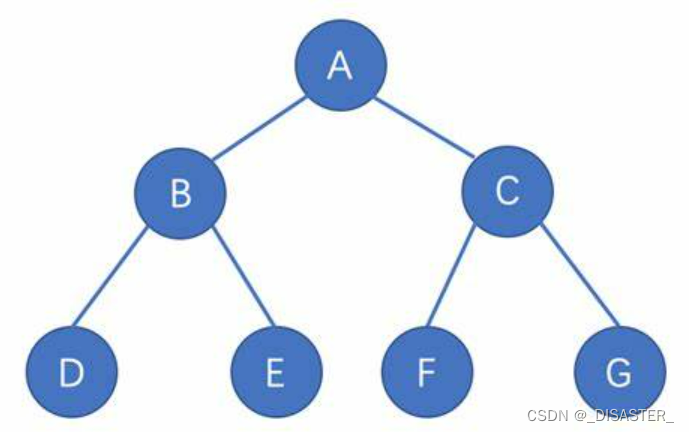
二叉树如其名,就是有两个分岔树枝的树,如下图。每个节点下面都有两个及两个以下的节点,就被称为二叉树。

二叉树的概念:
在每一个节点中都会有一个节点指向该节点,指向该节点的节点称为父节点。其中若没有节点指向该节点,则称该节点为根节点。
若有某节点指向当前节点,则称有入度。若当前节点存在指向的节点,则称有出度。二叉树的入度的数量与其父结点的数量有关(最多为1),二叉树的出度的数量与其子结点的数量有关(最多为2)。其中,入度与出度不可能小于0。
同时,每个节点都会指向两个及两个以下数量的节点,该节点指向的节点称为子节点,由于只有两个节点,他们也会被称为左节点和右节点或左孩子和右兄弟。
由于二叉树的性质,我们可以将二叉树看为一层一层的,通常将二叉树的层数称为高度。高度由上往下递增。二叉树每层最多只有个节点。
由于处于最高一层或次高层的部分节点没有子树,我们则将没有子树的节点称为叶子节点。
二叉树的遍历:
二叉树可以进行前序遍历、中序遍历、后序遍历及层序遍历。
前序遍历按照 根-左-右 的顺序进行遍历。
中序遍历按照 左-根-右 的顺序进行遍历。
后序遍历按照 左-右-根 的顺序进行遍历。
层序遍历按照层的从左到右的顺序进行遍历。
其中,若当前节点存在左右子节点,则会再次按照其遍历顺序进行遍历。

对于上图,其前序遍历是:A B D E C F G。
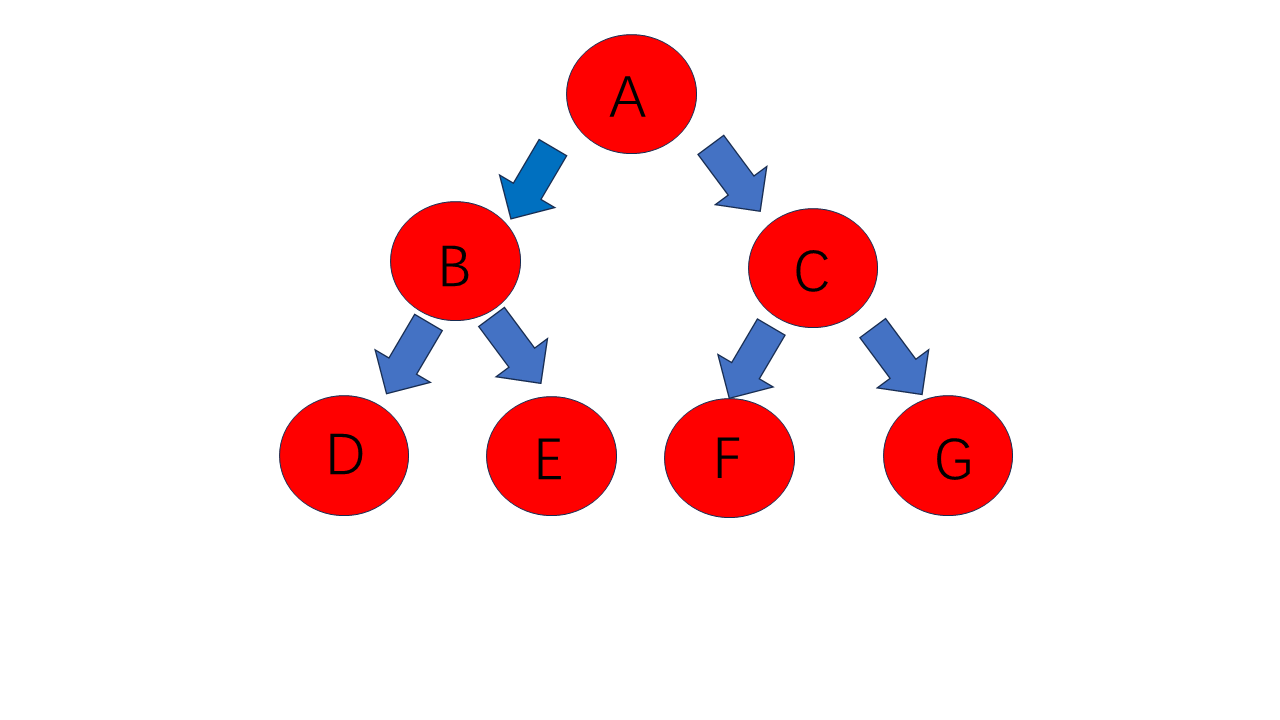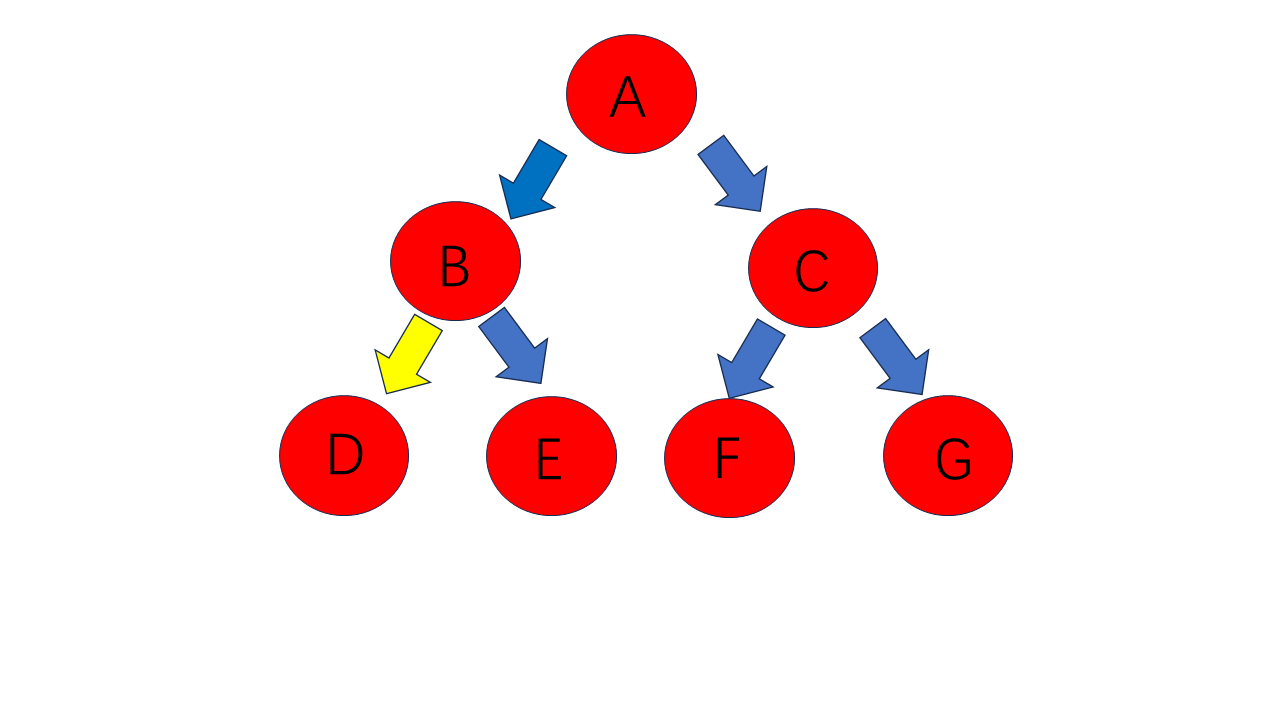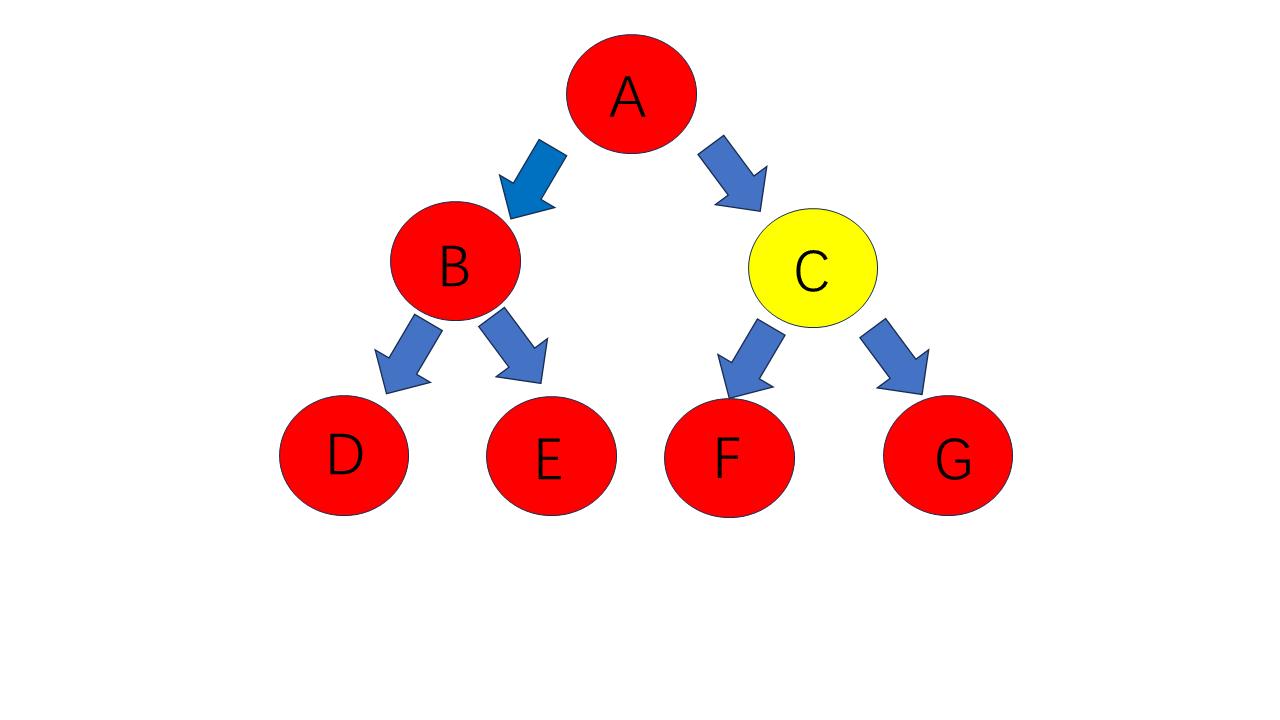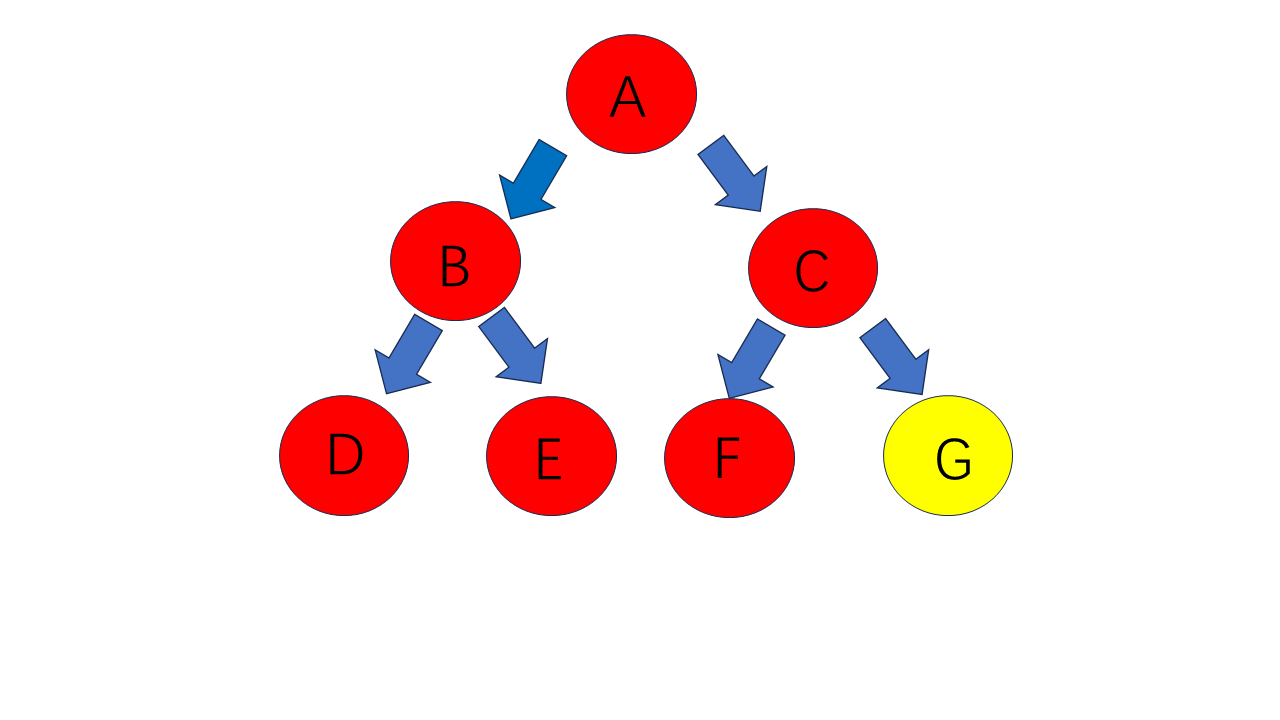
其中序遍历为:D B E A F C G
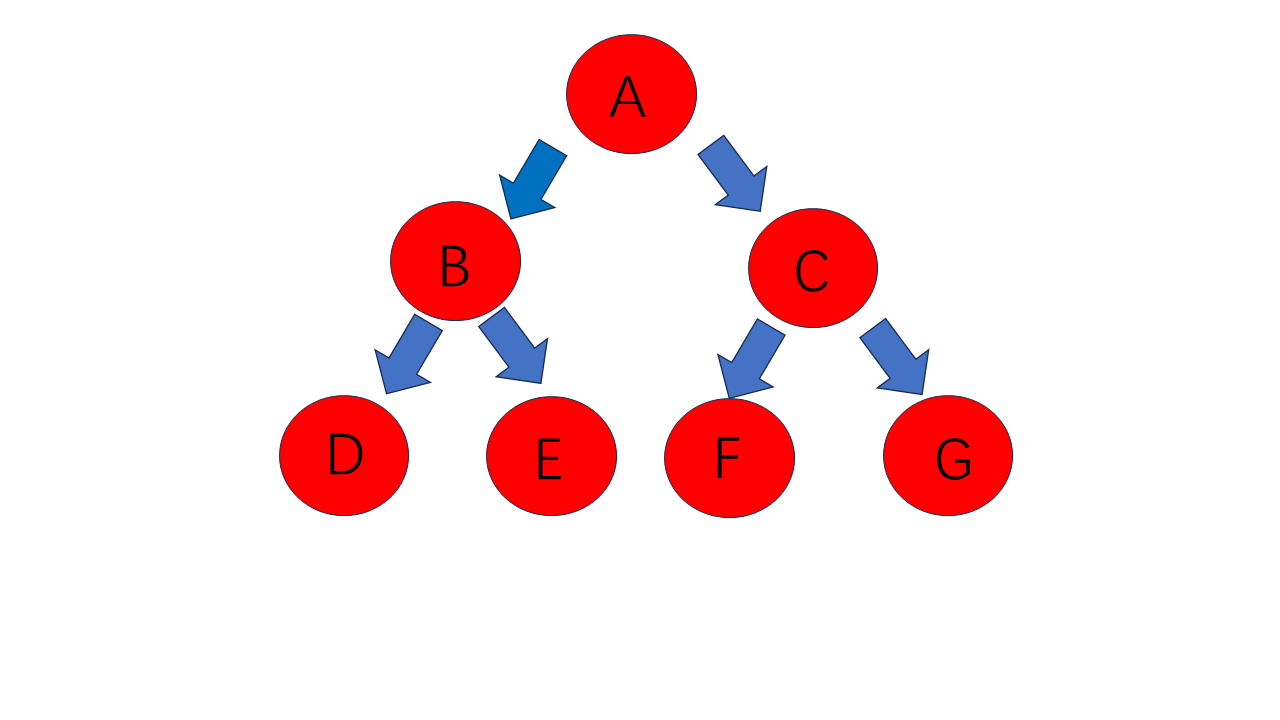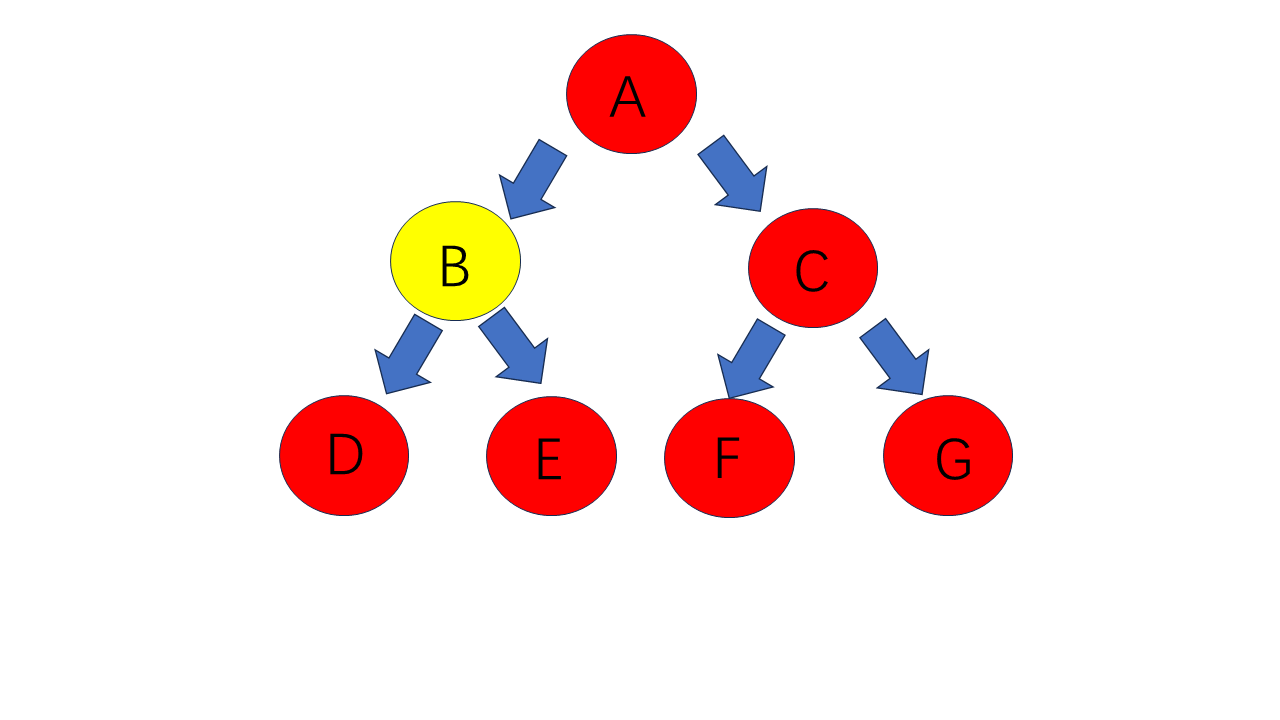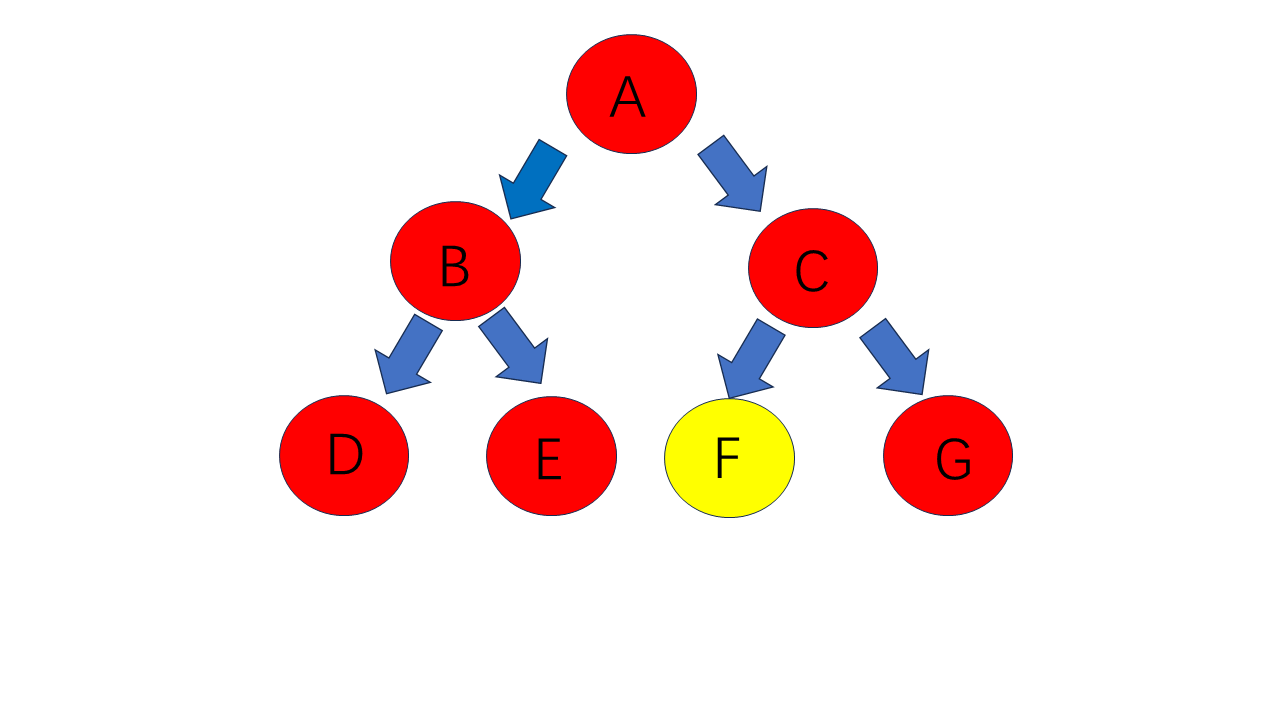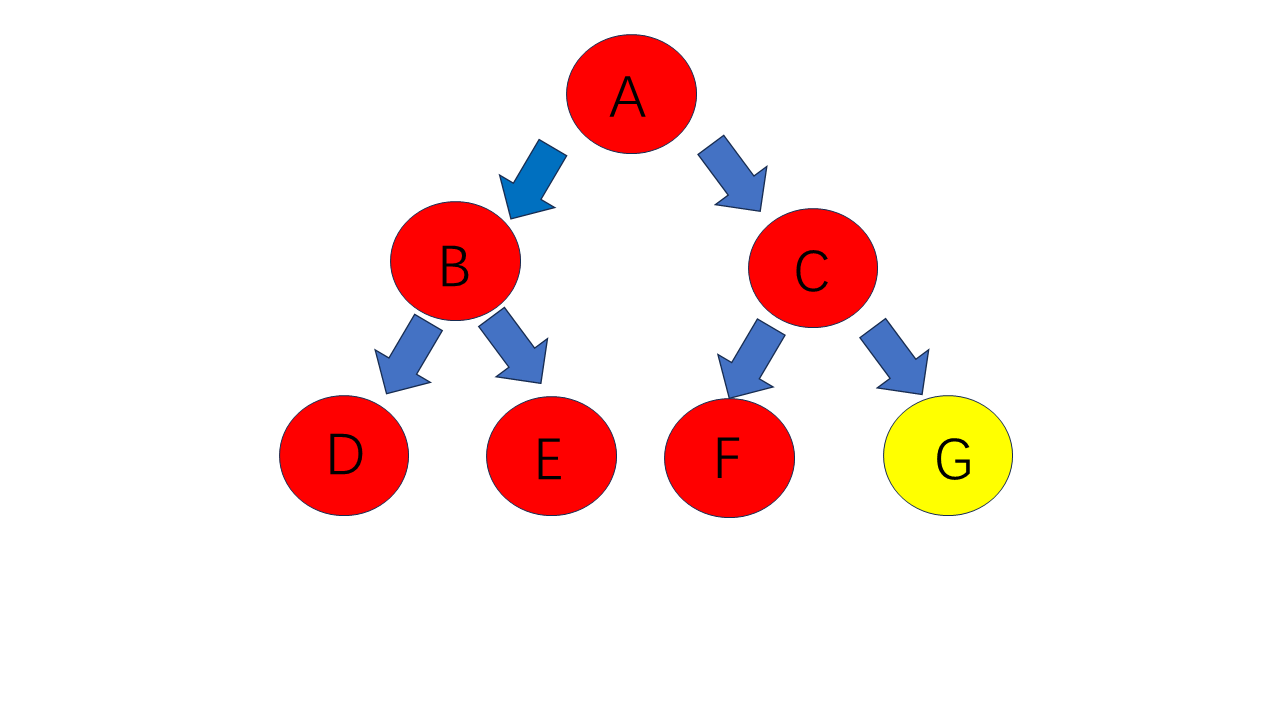
其后序遍历为:D E B F G C A
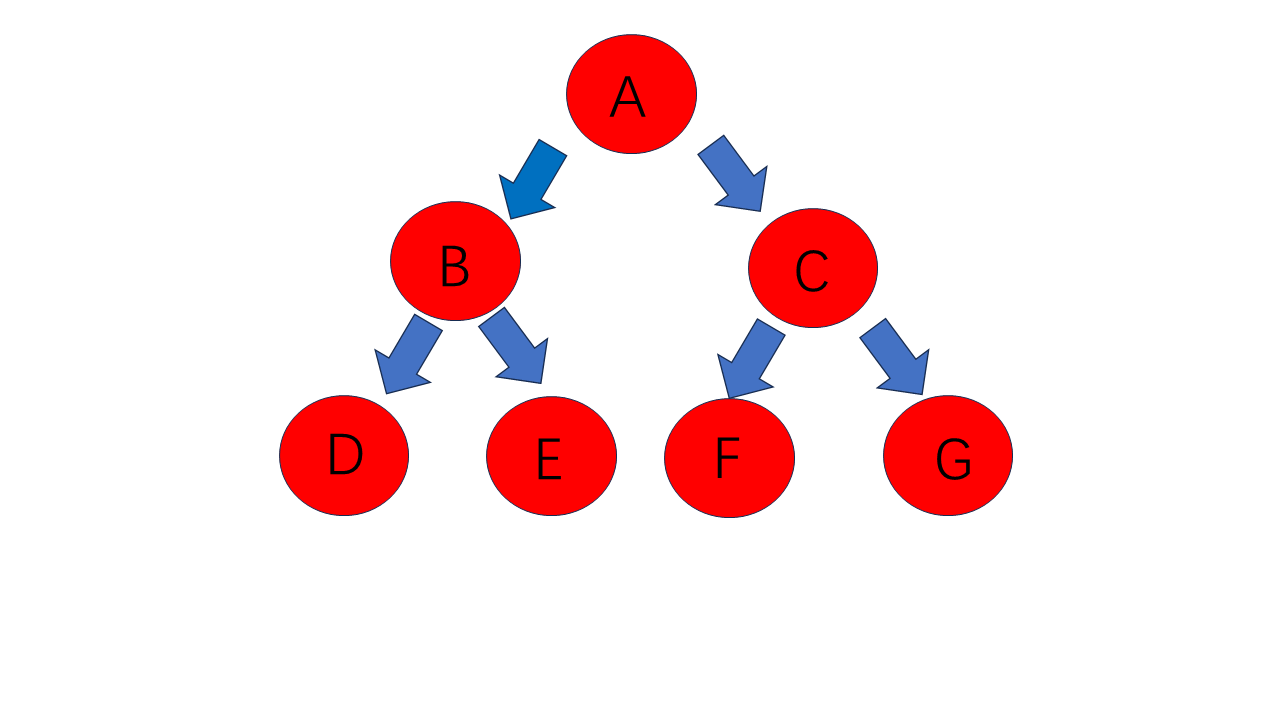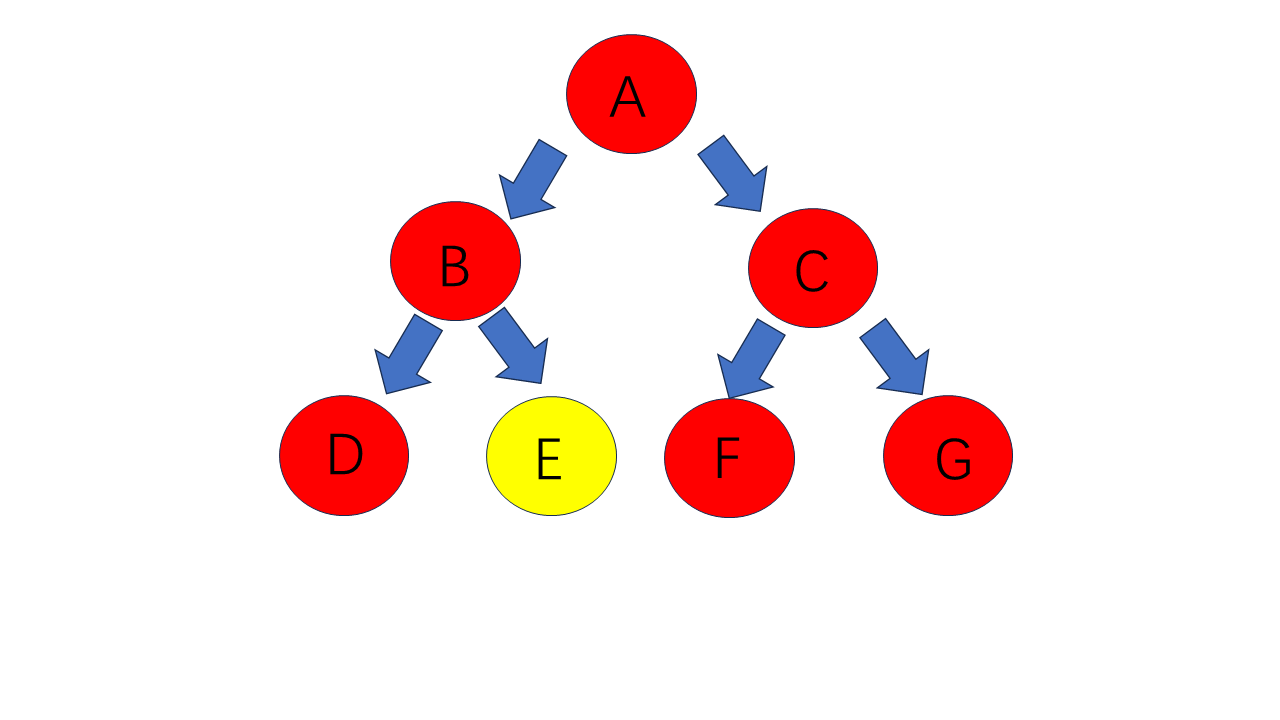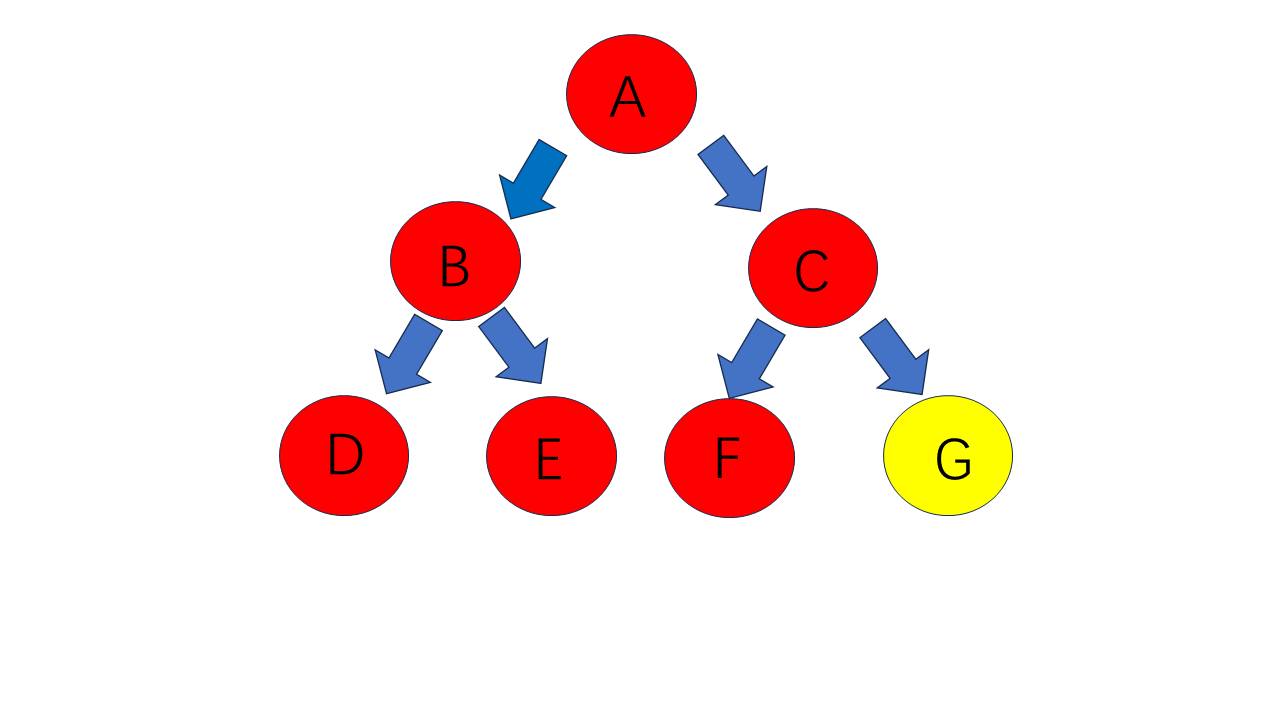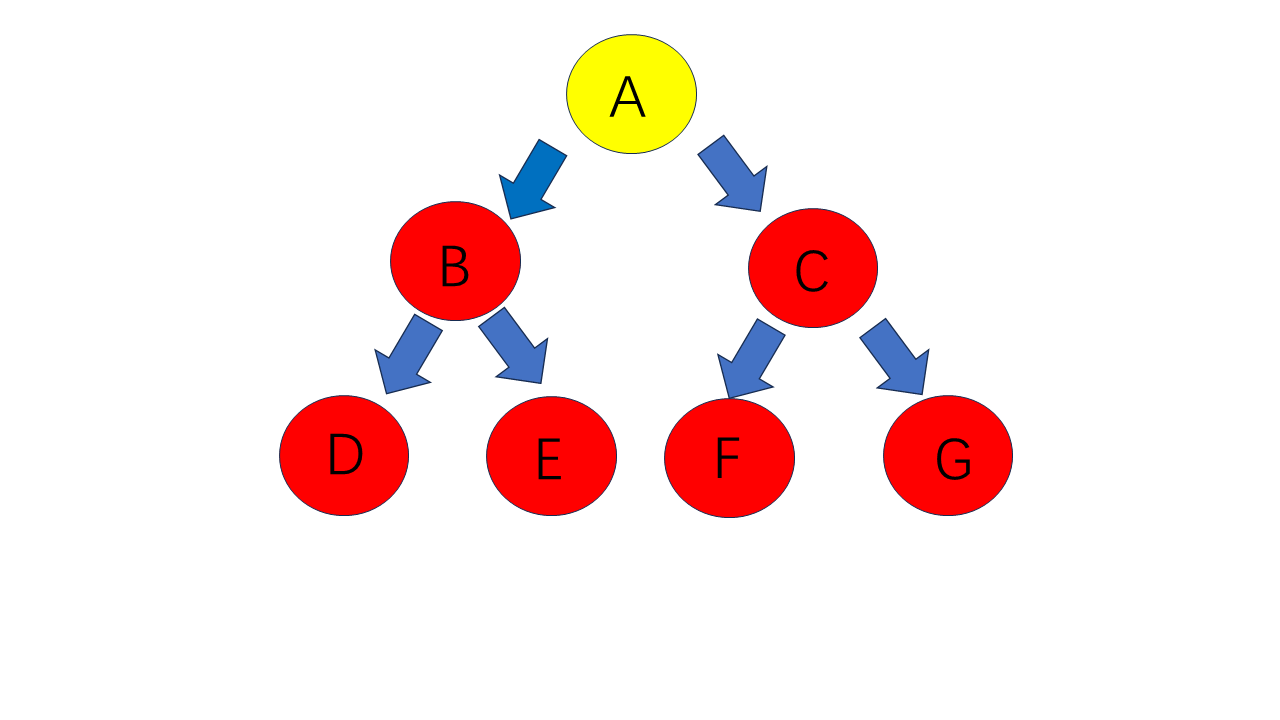
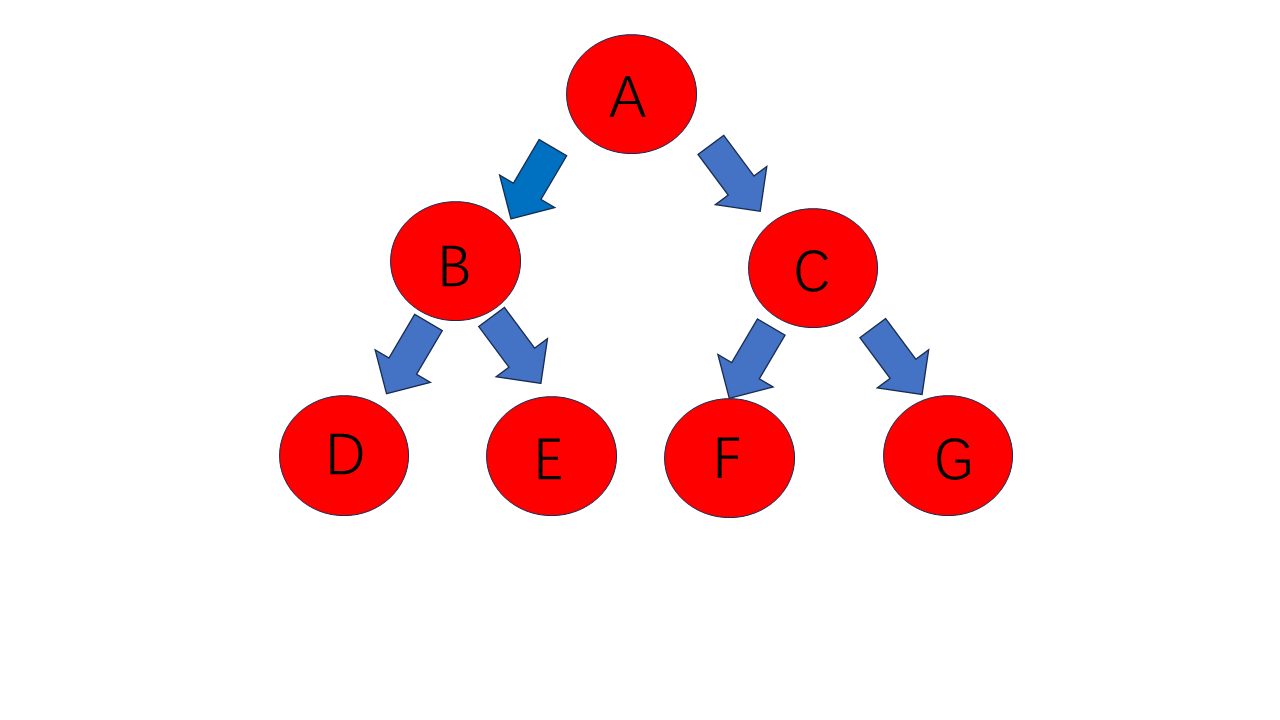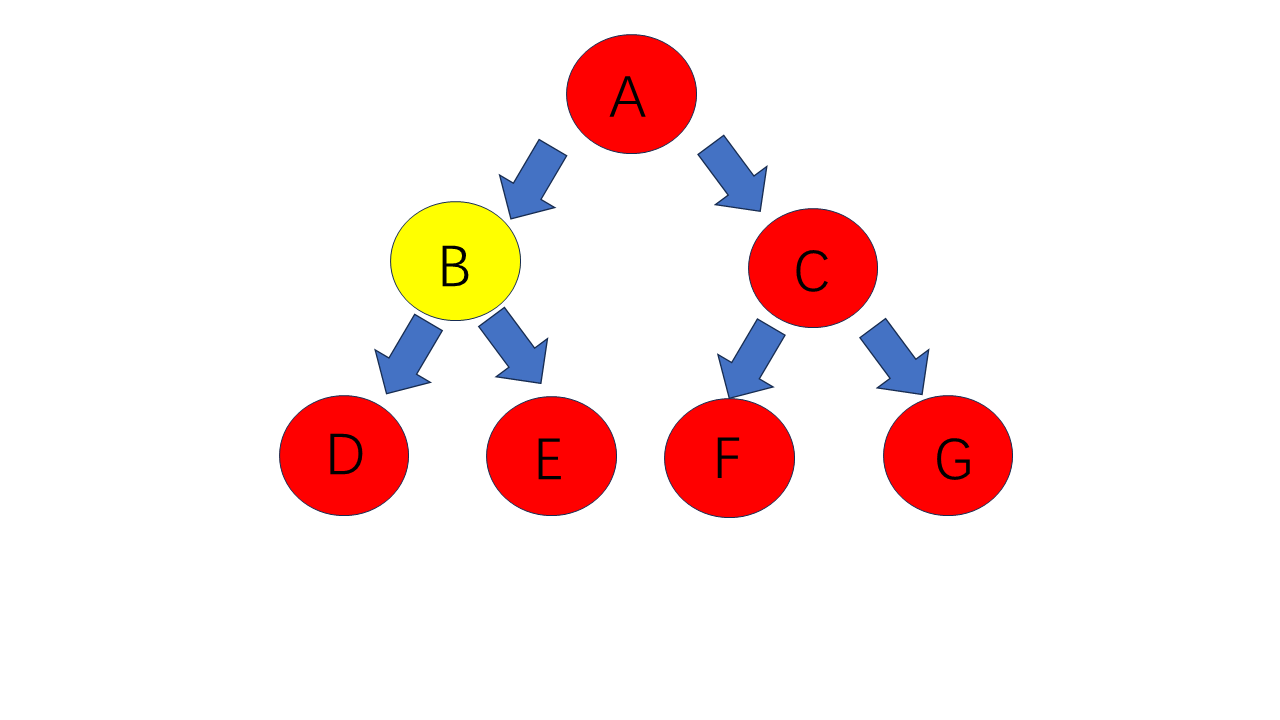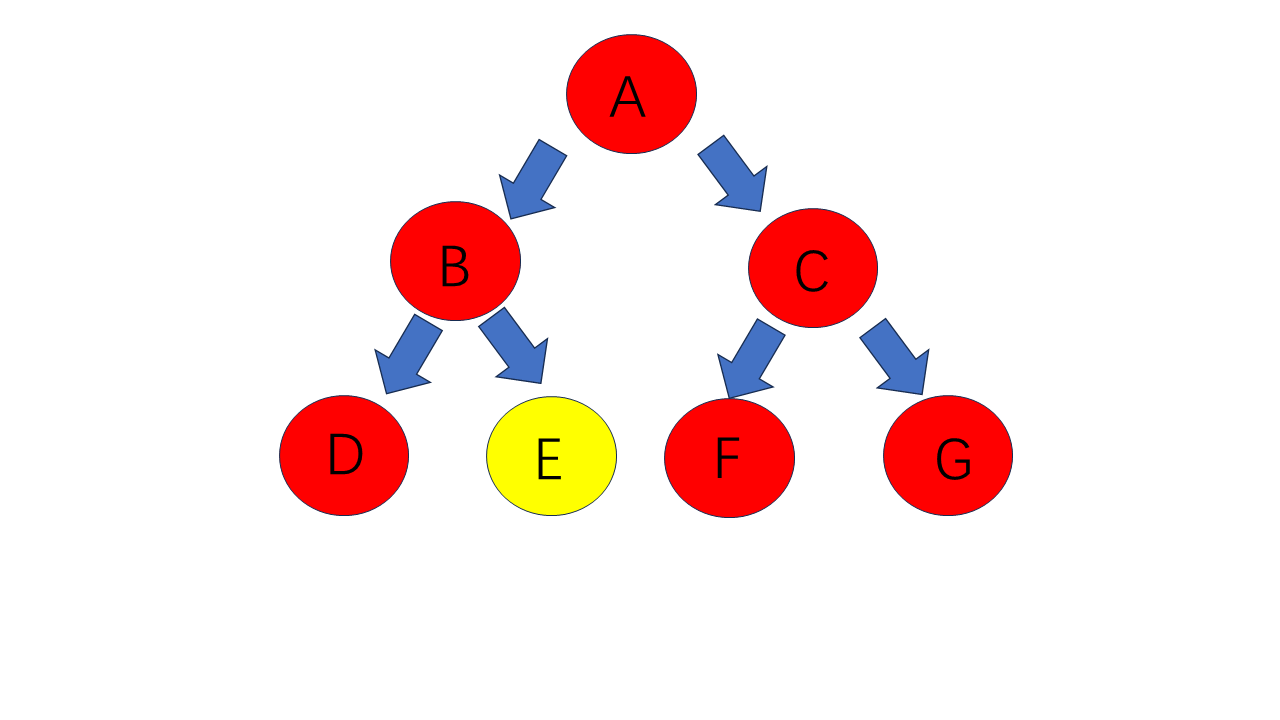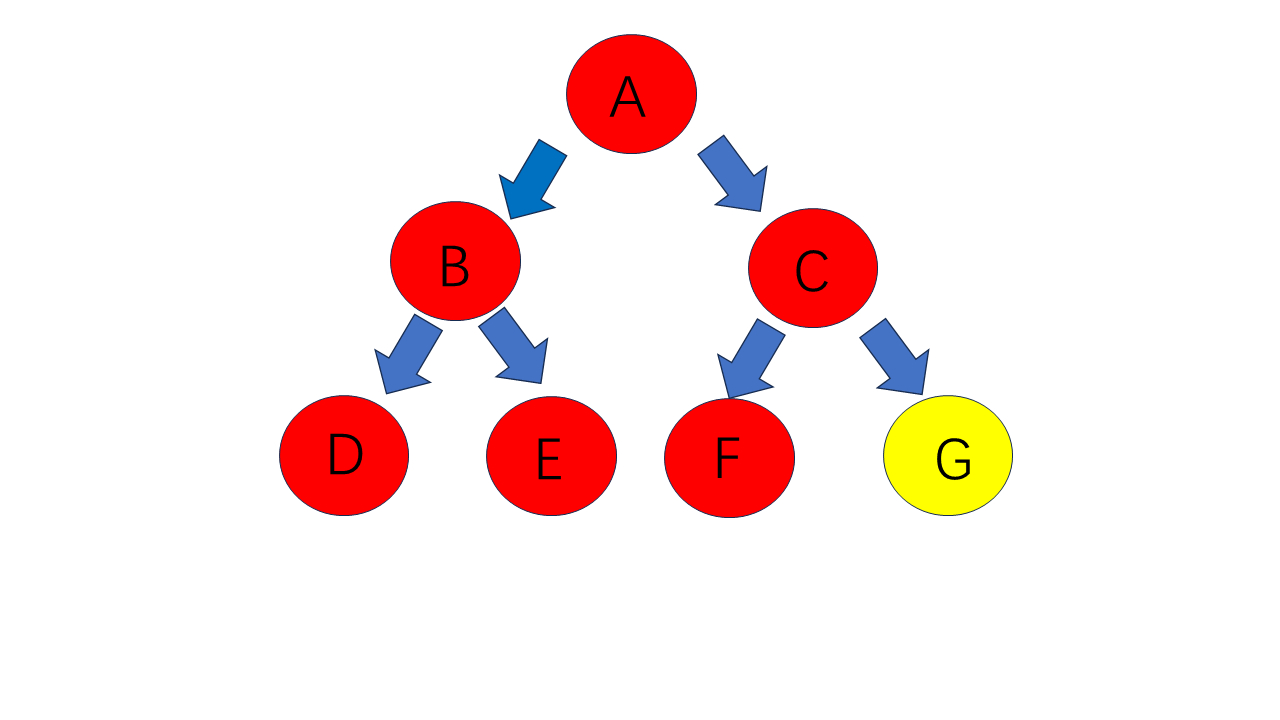
其层序遍历为:A B C D E F G
二叉树的种类:
二叉树可分为完全二叉树、满二叉树、AVL树和红黑树等。其中AVL树及进阶二叉树将在后续数据结构中进行讲解。
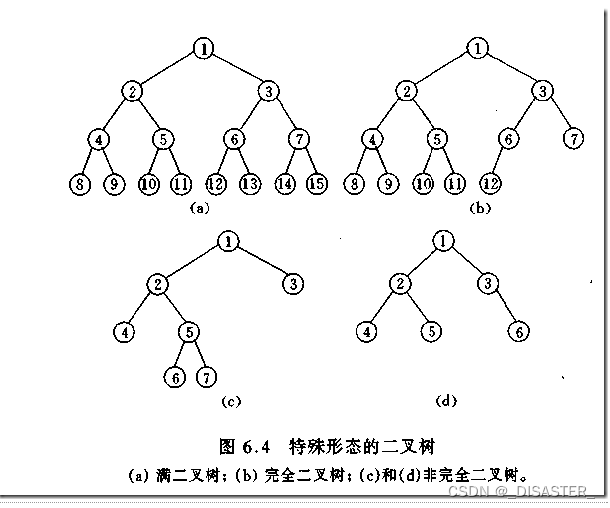
完全二叉树是指高度为h,叶子结点只可能在最下面的两层上出现且第 h 层所有的结点都连续集中在最左边的二叉树。若该完全二叉树拥有N个节点,则其高度不会超过层。下图中的b就是一个完全二叉树。
满二叉树是指对于高度为h的二叉树,其节点个数为个。下图中的a就是一个标准的满二叉树。
二叉树的特点:
在任意一颗二叉树中,若终端节点的个数为,度为2的节点数为
,则
=
+1。
二叉树的代码实现:
接下来是基于C语言的实现二叉树的增删查改功能。
二叉树的数据结构定义:
二叉树的每个节点中都需要存储一个数据,并且存储其两个子树的地址。
typedef struct tree {int data;tree* bro, * kid;
}tree;二叉树的初始化:
tree* Init_Tree(int val) {tree* p = (tree*)malloc(sizeof(tree));p->data = val;return p;
}二叉树的销毁:
由于我们使用了malloc函数实现了内存分配,所以我们需要将每一个节点都使用free函数释放掉。
void Free(tree* p) {if (p == NULL) {return;}Free(p->bro);Free(p->kid);free(p);return;
}二叉树的插入:
此处为随机往左右子树进行插入。
tree* Insert(tree* p, int val) {if (p == NULL) {return Init_Tree(val);}srand(time(0));if (rand() % 2 == 1) {p->kid = Insert(p->kid, val);}else {p->bro = Insert(p->bro, val);}return p;
}二叉树的前序遍历:
void Tree_Preorder(vector<string>& arr, tree* root) {if (root == NULL) {arr.push_back("#");}arr.push_back(to_string(root->data));Tree_Preorder(arr, root->kid);Tree_Preorder(arr, root->bro);return;
}二叉树的中序遍历:
void Tree_Inorder(vector<string>& arr, tree* root) {if (root == NULL) {arr.push_back("#");}Tree_Inorder(arr, root->kid);arr.push_back(to_string(root->data));Tree_Inorder(arr, root->bro);return;
}二叉树的后序遍历:
void Tree_Postorder(vector<string>& arr, tree* root) {if (root == NULL) {arr.push_back("#");}Tree_Inorder(arr, root->kid);Tree_Inorder(arr, root->bro);arr.push_back(to_string(root->data));return;
}二叉树的层序遍历(广度优先):
二叉树也可以按层进行遍历,我们称其为层序遍历或广度优先。
在二叉树的层序遍历中,我们需要用到队列的数据结构(不懂队列的同学可以看看我之前写的队列和栈的博客->)。首先将根节点放入队列中,当队列不为空时,依次取出队列中的每一个节点并且将其弹出队,将每一个节点的左右子树都放入队列中,以此实现二叉树的层序遍历。
void Tree_Levelorder(tree* p) {if (p == NULL) {return;}int head = 0, tail = 0;queue[tail++] = p;while (head<tail){tree* now = queue[head++];if (now->kid) {queue[tail++] = now->kid;}if (now->bro) {queue[tail++] = now->bro;}}return;
}最后一个问题为什么是二叉呢?不是单叉、三叉或者是四叉及以上呢?如果你知道答案,可以把答案发在评论中和大家讨论一下。






