
这道题如果没有时间复杂度的限制的话,相当好做,但是这道题要求时间复杂度为O(log(m + n)),思路很难想,我看了一圈题解,发现华南溜达虎的视频讲得还不错,我是参考他的思路写出来的,这里把他的思路记录一下。
对于两个升序排列的数组,我们只需要在两个数组中分别找到下标i和j,使得nums1[i]左侧的元素与nums2[j]左侧的元素个数之和最多比nums1[i]与nums2[j]及其右边的元素数量多1,则我们就找到了中位数,下面简单举个例子。
 对于上面两个数组,我们通过寻找合适的下标
对于上面两个数组,我们通过寻找合适的下标i和j,使得左侧的元素个数为5。
对于上面的数组,元素个数为10,所以剩下的元素也为5个,针对这种情况,我们只需要选出红色圈内的最大值(max(nums1[i - 1], nums2[j - 1])),再选出右侧元素中的最小值(min(nums1[i], nums2[j])),再求平均值即可求出中位数。
对于下面的数组,元素个数为9,所以剩下的元素个数为4个,针对这种情况,我们只需要选出红色圈内的最大值,即可求出中位数。
那么,我们如何选出合适的i和j呢?我这里就直接引用作者的约束了。
1. nums1[i - 1] < nums1[i]
2. nums2[j - 1] < nums2[j]
3. nums1[i - 1] < nums2[j]
4. nums2[j - 1] < nums1[i]
第一条和第二条约束是为了保证两个数组都是递增的,在本题显然成立,因此不用开率;第三条和第四条则确保了nums1[i]和nums2[j]左侧的所有元素恰好为合并数组中的前一半元素。在满足以上性质以后,我们可以进行进一步分析,左侧的元素可以用一根线串起来,如下所示。

用绳子将左侧的所有元素穿起来,绳子两头的右边一位就是对应的元素下标i和j,同时我们不难发现,无论元素总数为奇数还是偶数,绳子上的元素个数均等于i + j,因此我们一旦确定了i,j也随之确定了。我们要做的就是在nums1中找到i,然后就能找到中位数。我们在初始化时,默认将i设置为nums1的中间位置,然后j通过绳子的长度-i得到。上面的第三条和第四条性质并不总是同时满足,但是一定不会同时不满足,这是两个数组均为递增数组的性质决定的。当第三条性质不满足时,则说明上面的线太长,而下面的线太短,此时我们需要将上面的线头向左移,当第四条性质不满足时,说明下面的线太长,而上面的线太短,此时我们需要将上面的线头向右移。当同时满足以上四条性质时,则找到了合适的位置。以上说的是最常见的情况,也就是绳子的两端可以落在两个数组中间的情况,下面我们来看一下绳子落在数组边界之外的情况:
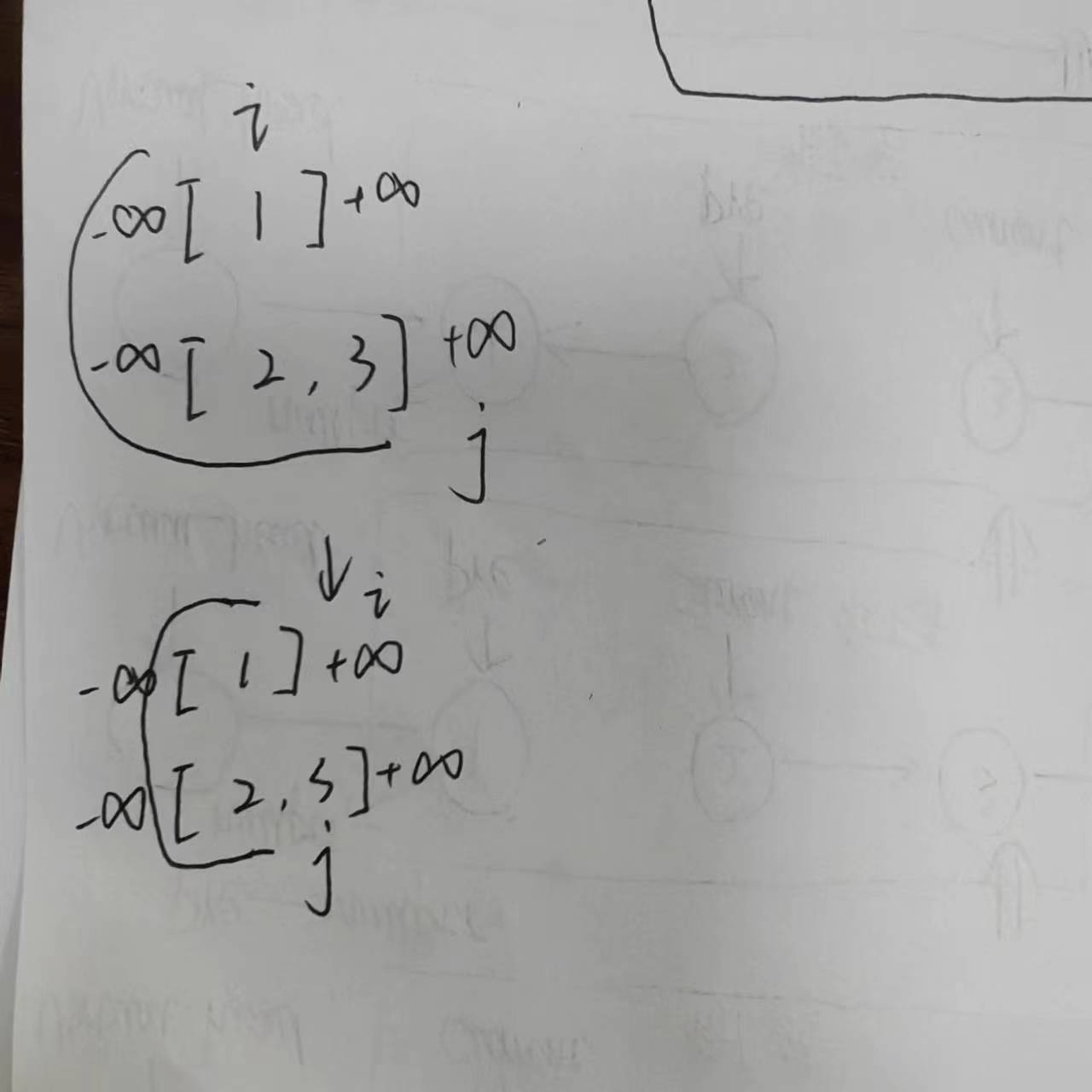
当我们进行初始化时,i = (0 + nums1.size()) / 2,为0,此时j的初始位置发生了越界。当我们找到合适的i和j后,我们发现此时i发生了越界,此时线上的元素为[1, 2],我们返回其中的较大值作为中位数。但是我们是怎么从初始状态转移到最终的状态的呢?在初始状态下,i的左边没有元素,在判断条件三的时候显然会发生越界访问,此时我们观察到条件四也不满足,为了维护上述性质的成立,3和4只能由一条不成立,条件四不成立是板上钉钉的事实,我们需要执行条件四的维护操作,而条件三应当想办法使其成立,在这种情况下,应当假设i左边存在一个元素(仅在发生左边越界的时候才会出现),无论nums[j]为何值,都有nums1[i - 1] < nums2[j]成立,所以应当假设数组的左侧有INT_MIN,当发生左侧越界时,则用INT_MIN来代替nums[i - 1],当nums2发生左侧越界时也是同理。当发生右侧越界时,我们采用INT_MAX来代替越界的值。
感觉这道题目还是很晦涩难懂,真的好难想╮(╯▽╰)╭
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {if(nums1.size() > nums2.size())swap(nums1, nums2); //确保nums1总是较短的那个数组int m = nums1.size();int n = nums2.size();int left = 0, right = m; //在nums1中进行二分查找while(left <= right){int i = (left + right) / 2;int j = (m + n + 1) / 2 - i; //绳子的长度为(m + n + 1) / 2int left1 = (i == 0) ? INT_MIN : nums1[i - 1];int right1 = (i == m) ? INT_MAX : nums1[i];int left2 = (j == 0) ? INT_MIN : nums2[j - 1];int right2 = (j == n) ? INT_MAX : nums2[j];if(left1 <= right2 && left2 <= right1){if((m + n) % 2 == 1)return max(left1, left2);return (min(right1, right2) + max(left1, left2)) / 2.0;}else if(left1 > right2)right = i - 1;else left = i + 1;}return 0;}
};

)

)



