70、爬楼梯

题目

动态规划：爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶
   示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

1 <= n <= 45

代码

class Solution {
public:int climbStairs(int n) {int pre1=1,pre2=1;int cur=1;for(int i=2;i<=n;i++){cur=pre1+pre2;int temp=pre1;pre1=cur;pre2=temp;}return cur;}
};

原理图与原理解释

递归方法：超出时间限制

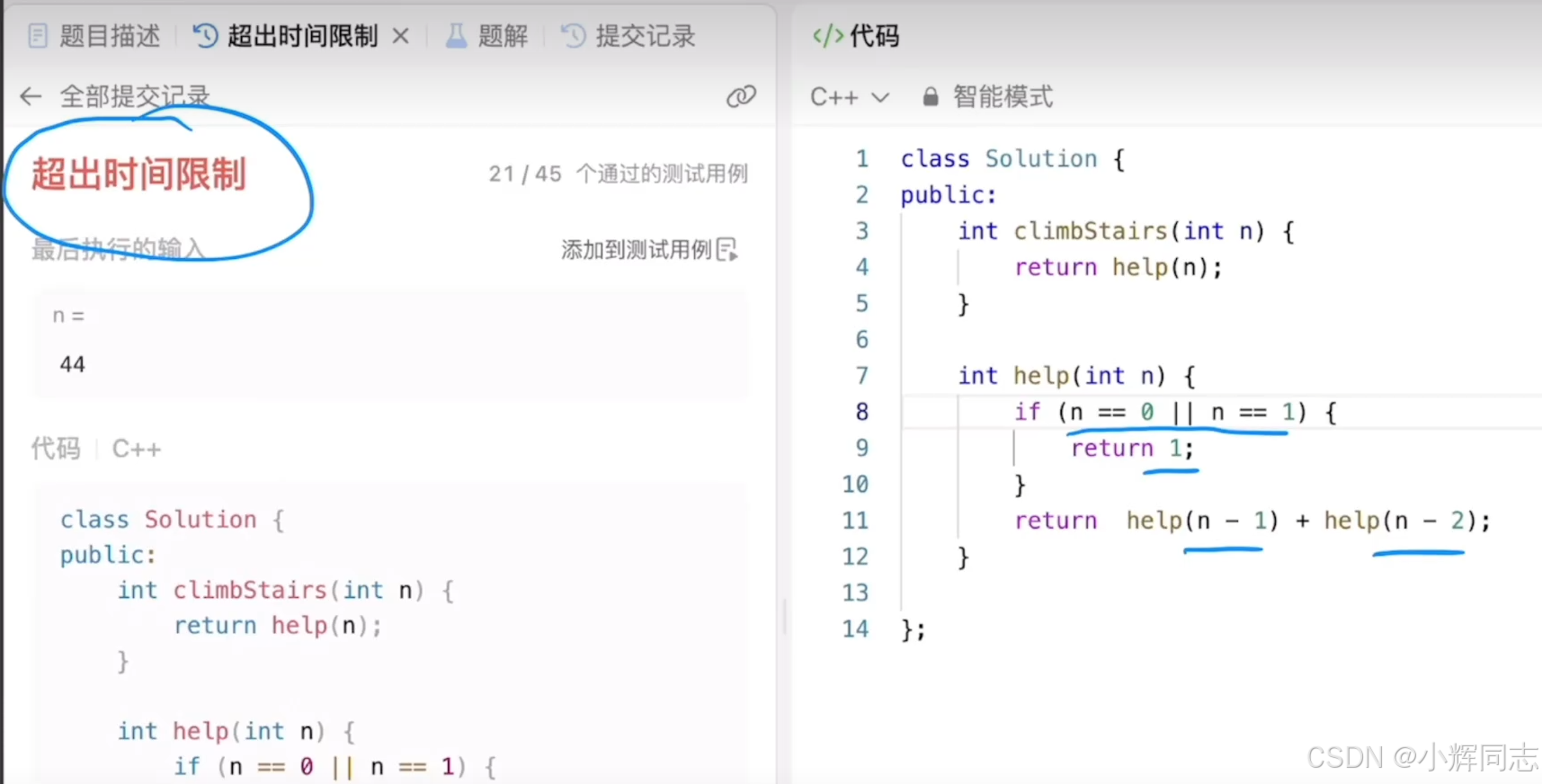
其中包含了很多重复计算的问题，比如爬一阶重复计算了三次，二阶重复计算了两次，使用一个备忘录递归的方式可以节省不必要的计算，缩短时间。整个递归的过程是自上而下的过程，而填写备忘录的过程是一个自下而上的过程。这种把原问题划分为独立的子问题，并对子问题自下而上记忆存储的过程就是使用动态规划解决问题的过程。

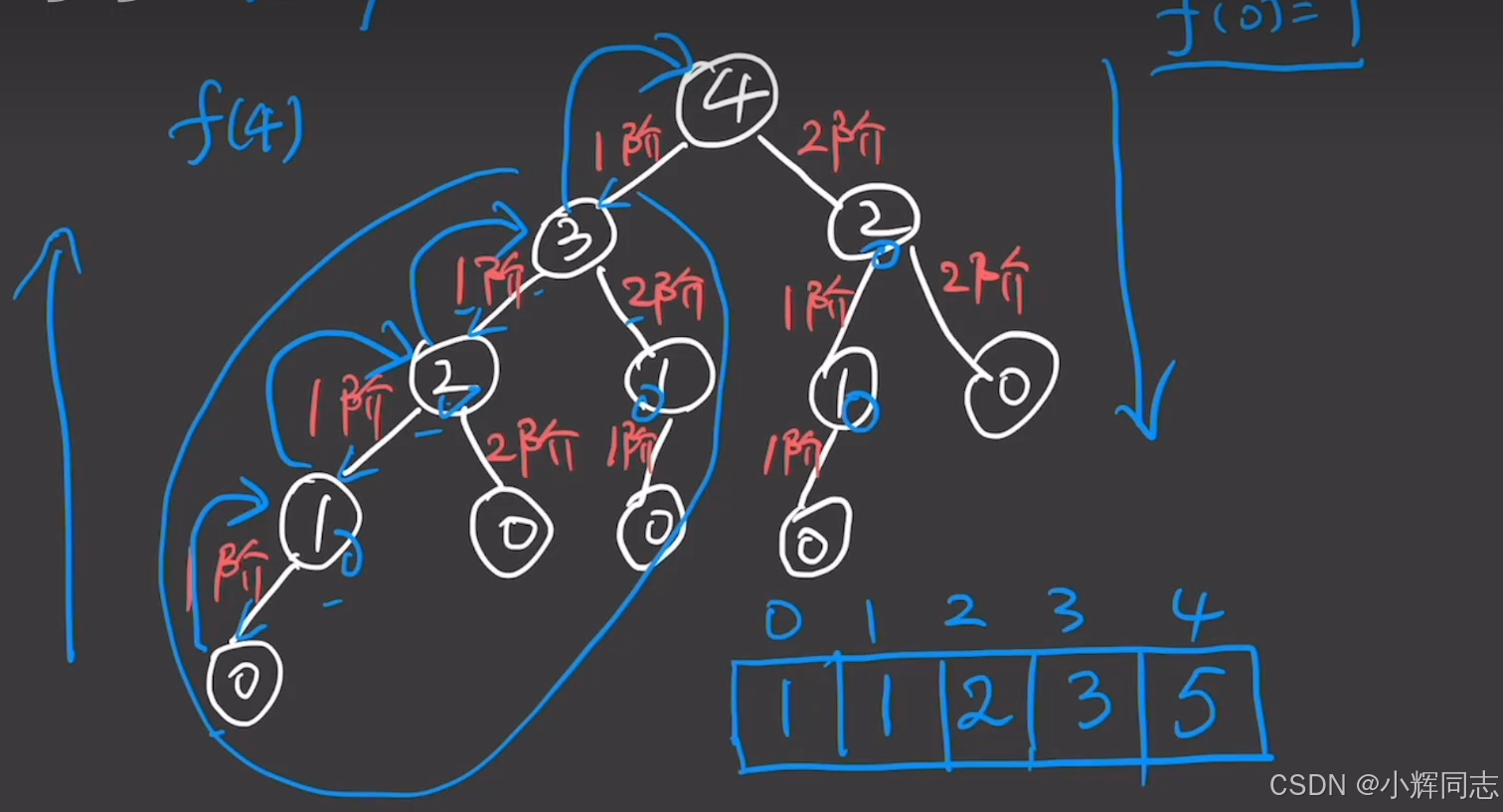
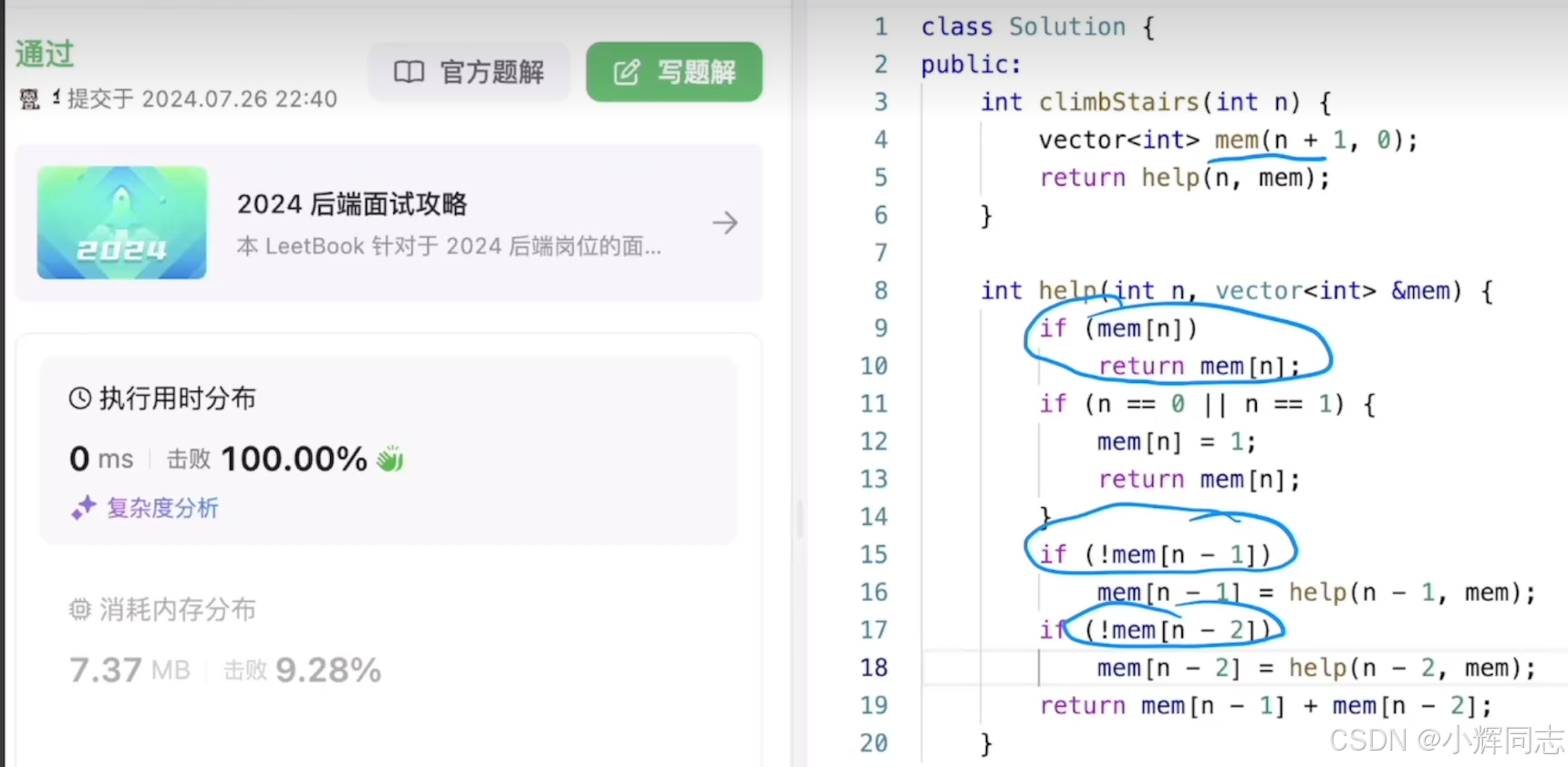
另一种方法是不使用递归，使用一种迭代的方式，根据状态转移方程和边界条件给出迭代形式的代码

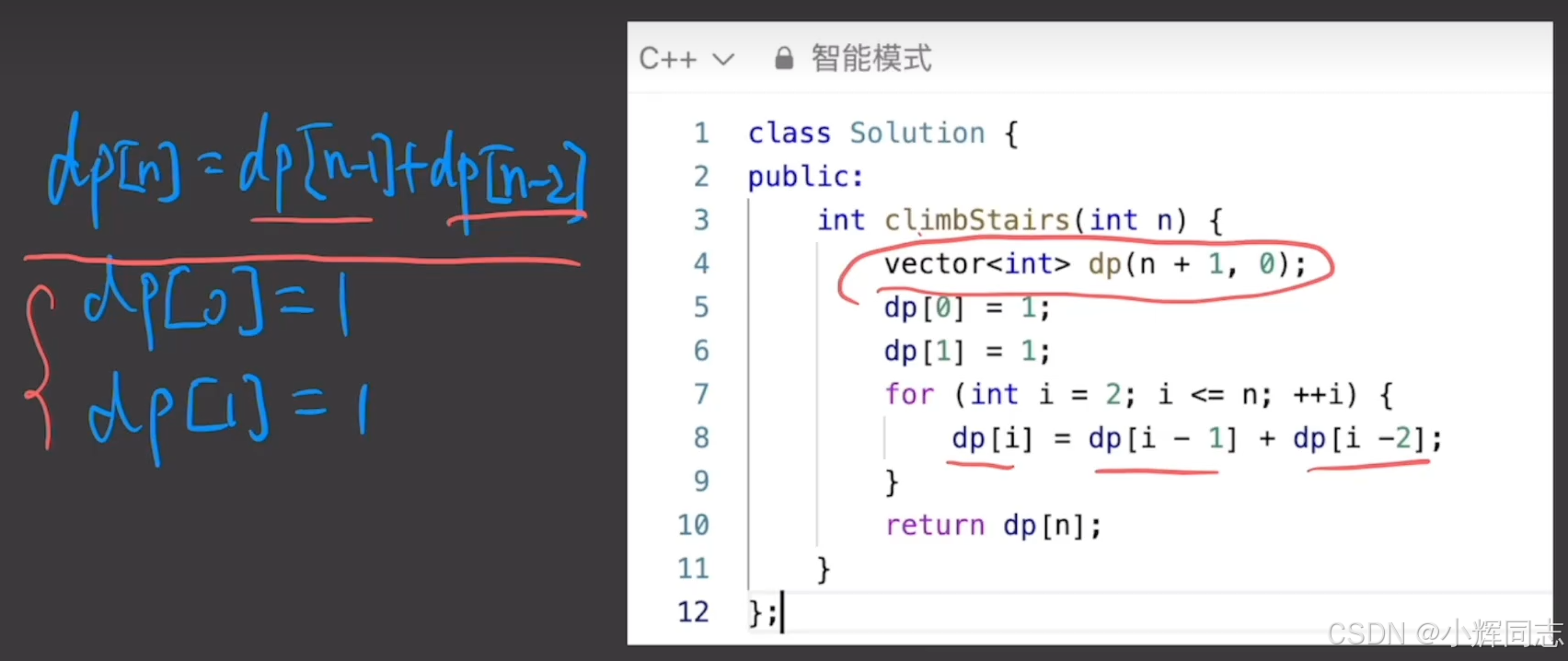
也可以不使用数组，仅使用两个变量，只需要保存前面两个状态的值，空间复杂度为O(1)
优化后的代码：

遇到问题先写递归，然后再看是否能改造成自上而下的带备忘录的递归，最后再看是否可以优化成自下而上的迭代。

结束

原理图借鉴哔站华南溜达虎，如有侵权联系删除。