有两种形状的瓷砖:一种是 2 x 1 的多米诺形,另一种是形如 “L” 的托米诺形。两种形状都可以旋转。
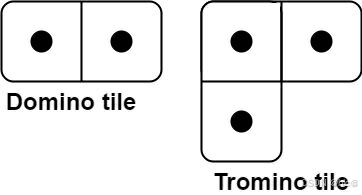
给定整数 n ,返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。
平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同,当且仅当面板上有四个方向上的相邻单元中的两个,使得恰好有一个平铺有一个瓷砖占据两个正方形。
示例 1:
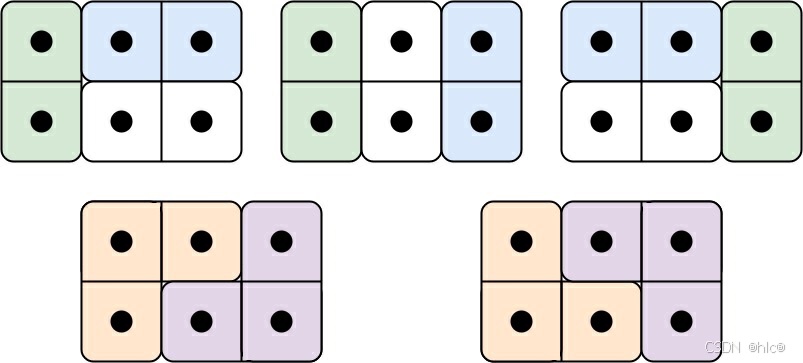
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。
示例 2:
输入: n = 1
输出: 1
提示:
1 <= n <= 1000
动态规划
class Solution {
public:int numTilings(int n) {int MOD = 1e9 + 7;//0:一个都没有覆盖//1:只有上方覆盖//2:只有下方覆盖//3:都被覆盖vector<vector<long long>> dp(n+1, vector<long long>(4));dp[0][3] = 1;for(int i = 1; i <= n; i++){dp[i][0] = dp[i-1][3] % MOD;dp[i][1] = (dp[i-1][0] + dp[i-1][2]) % MOD;dp[i][2] = (dp[i-1][0] + dp[i-1][1]) % MOD;dp[i][3] = (dp[i-1][0] + dp[i-1][1] + dp[i-1][2] + dp[i-1][3]) % MOD;}return dp[n][3];}
};
时间复杂度:O(n),其中 n 是总列数。
空间复杂度:O(n)。保存 dp 数组需要 O(n) 的空间。
我们可以根据题目来定义一个二维数组dp[i][s],他的状态s有四种:
一个正方形都没有被覆盖,记为状态 0;
只有上方的正方形被覆盖,记为状态 1;
只有下方的正方形被覆盖,记为状态 2;
上下两个正方形都被覆盖,记为状态 3。
使用 dp[i][s] 表示平铺到第 i 列时,各个状态 s 对应的平铺方法数量。考虑第 i−1 列和第 i 列正方形。

举个例子,如果在铺第i列的时候,我们铺完后第i列只有上面方块被覆盖,也就是dp[i][1],那么如图可以知道,我们如果第i-1列没有任何方块,那么它可以用一个倒L来使得第i-1列全部被覆盖,并且第i列的上面方块被覆盖。或者第i-1列只有下面方块被覆盖,我们可以使用一个横着的两格砖块来使第i-1列全部被覆盖并且第i列的上面方块被覆盖。
所以我们可以得到所有情况的状态转移方程,最后返回dp[n][3]即可。






