【C】初阶数据结构11 -- 选择排序

2025/5/3 17:34:10 来源：https://blog.csdn.net/L_0907/article/details/144494789 浏览: 次关键词：【C】初阶数据结构11 -- 选择排序

本篇文章主要讲解经典排序算法 -- 选择排序

1 算法思想

2 代码

3 时间复杂度与空间复杂度分析

1）时间复杂度

2）空间复杂度

1 算法思想

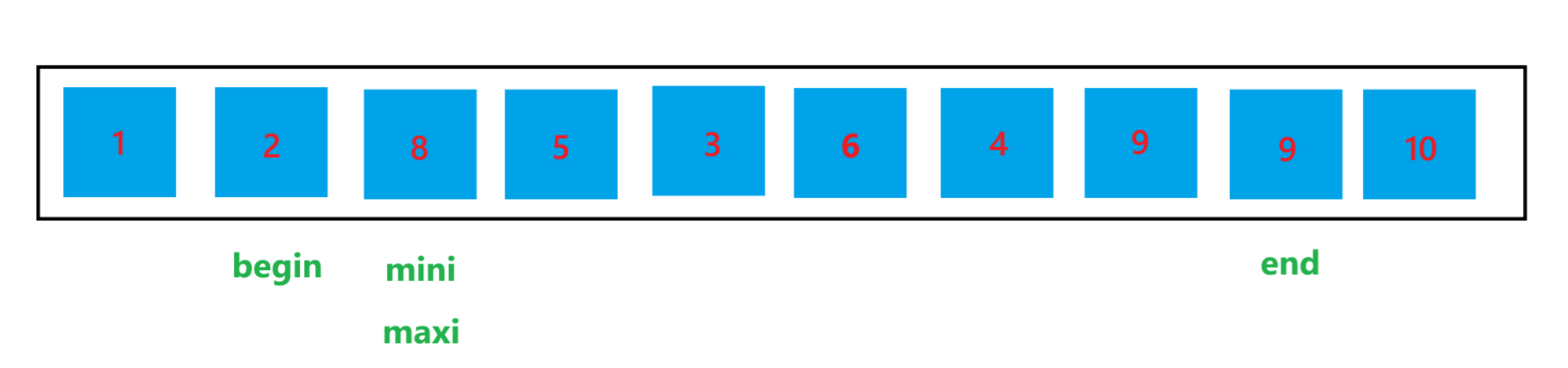
选择排序是一种在一段区间里面选择最小的元素和最大的元素的一种排序算法。假设这里排升序，首先标记第一个元素的下标为 begin ，最后一个元素的下标为 end，然后在 [begin, end] 区间里选择最小的元素 mini 和最大的元素 maxi，然后将 begin 位置元素和 mini 位置元素交换，再将 maxi 和 end 位置元素交换，再将区间缩小，即 begin++，end--，再循环上述过程，直到 begin >= end。选择排序的过程如图所示：

但是选择排序里面有一种特殊情况，就是当 maxi 元素和 begin 元素为一个元素时，需要让 maxi 先等于 mini，再让 mini 位置元素和 begin 位置元素，maxi 位置和 end 位置元素交换，否则排序的结果会出现错误，例如下图所示：

此时 maxi 元素为 9，与 begin 位置元素重合，如果不使 maxi = mini 的话，会出现如下结果：
此时，并不是将最大元素 9 交换到了 end 位置，而是将最小元素 2 交换到了 end 位置，会导致排序结果混乱，所以要先让 maxi = mini，再交换：

2 代码

void Swap(int*x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void SelectSort(int* arr, int n)
{int begin = 0;int end = n - 1;while (begin < end){int mini = begin, maxi = end;//mini找最小的数据，maxi找最大的数据for (int i = begin;i <= end; i++){if (arr[mini] > arr[i])mini = i;if (arr[maxi] < arr[i])maxi = i;}//如果maxi与begin相同的话，要让maxi走到mini的位置if (maxi == begin)maxi = mini;Swap(&arr[begin], &arr[mini]);Swap(&arr[end], &arr[maxi]);begin++;end--;}
}

解释：开始先让 begin 指向第一个元素，让 end 指向最后一个元素，然后循环判断begin < end，在每次循环里面设置两个下标，让 maxi 指向 [begin, end] 区间内的元素的最大值，mini 指向 [begin, end] 区间内元素的最小值；然后处理一下特殊情况，当 maxi == begin 时，maxi = mini，之后交换 begin 和 mini 位置元素，交换 end 和 maxi 位置元素；最后缩小区间，让 begin++，end--，进行下一轮循环。

测试用例：

void Print(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}int main()
{int arr[] = { 10, 2, 5, 7, 1, 4, 8, 9, 6};int n = sizeof(arr) / sizeof(arr[0]);SelectSort(arr, n);Print(arr, n);return 0;
}

3 时间复杂度与空间复杂度分析

1）时间复杂度

通过代码我们可以很容易看出，选择排序共有两次循环，最外层循环的停止条件为 begin < end，也就是最外层循环会执行 n/2 次；然后里面又嵌套了一层 for 循环，执行次数为 end - begin + 1 次，最坏情况也就是最开始 begin 为0，end 为 n-1 次的时候，会执行 n 次，所以选择排序的时间复杂度 T(n) = O(n^2) 的。