一.斐波那契数列模型
1137. 第 N 个泰波那契数

class Solution {
public:int tribonacci(int n) {int t[100];t[0]=0;t[1]=t[2]=1;if(n<=0) return 0;else{ if(n<=2) return 1;else if(n==3) return 2;else{for(int i=3;i<=n;i++){t[i]=t[i-1]+t[i-2]+t[i-3];}}}return t[n];}
};⾯试题 08.01. 三步问题

class Solution {
public:int waysToStep(int n) {vector<long long>dp(n+1);if(n==1) return 1;else if(n==2) return 2;else if(n==3) return 4;else{dp[1]=1;dp[2]=2;dp[3]=4;for(int i=4;i<=n;i++){// dp[i]=(((dp[i-1]%1000000007)+dp[i-2])%1000000007+dp[i-3])%1000000007;dp[i]=(dp[i-1]+dp[i-2]+dp[i-3])%1000000007;}}return dp[n];}
}; 746. 使⽤最⼩花费爬楼梯

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int>dp(n+1);for(int i=2;i<=n;i++){dp[i]+=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[n];}
};91. 解码⽅法
dp[i]表示:以i位置为结尾时,解码方法的总数

class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int>dp(n);dp[0]=s[0]!='0';if(n==1) return dp[0];if(s[1]<='9'&&s[1]>='1') dp[1]+=dp[0];int ret=(s[0]-'0')*10+s[1]-'0';if(ret>=10&&ret<=26) dp[1]+=dp[0];for(int i=2;i<n;i++){if(s[i]<='9'&&s[i]>='1') dp[i]+=dp[i-1];int r=(s[i-1]-'0')*10+s[i]-'0';if(r>=10&&r<=26) dp[i]+=dp[i-2];}return dp[n-1];}
};二.路径问题
62. 不同路径
dp[i][j]:走到[i,j]位置时,一共多少种方式


class Solution {
public:int uniquePaths(int m, int n) {//1.创建dp表vector<int>dpp(n+2);vector<vector<int>>dp(m+2,dpp);dp[0][1]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}
};63. 不同路径 II

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m=obstacleGrid.size();int n=obstacleGrid[0].size();vector<vector<int>>dp(m+1,vector<int>(n+1));dp[0][1]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=obstacleGrid[i-1][j-1];if(dp[i][j]==1) dp[i][j]=0;else dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}
};LCR166.珠宝的最高价值

class Solution {
public:int jewelleryValue(vector<vector<int>>& frame) {int m=frame.size();int n=frame[0].size();vector<vector<int>>dp(m+1,vector<int>(n+1));for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=frame[i-1][j-1]+max(dp[i-1][j],dp[i][j-1]);}}return dp[m][n];}
};931. 下降路径最⼩和


class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int n=matrix.size();vector<int>dpp(n+2,INT_MAX);vector<vector<int>> dp(n+1,dpp);for(int j=0;j<=n+1;j++){dp[0][j]=0;}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dp[i][j]=min(dp[i-1][j+1],min(dp[i-1][j-1],dp[i-1][j]))+matrix[i-1][j-1];}}int mn=INT_MAX;for(int i=1;i<=n;i++){mn=min(mn,dp[n][i]);}return mn;}
};64. 最⼩路径和

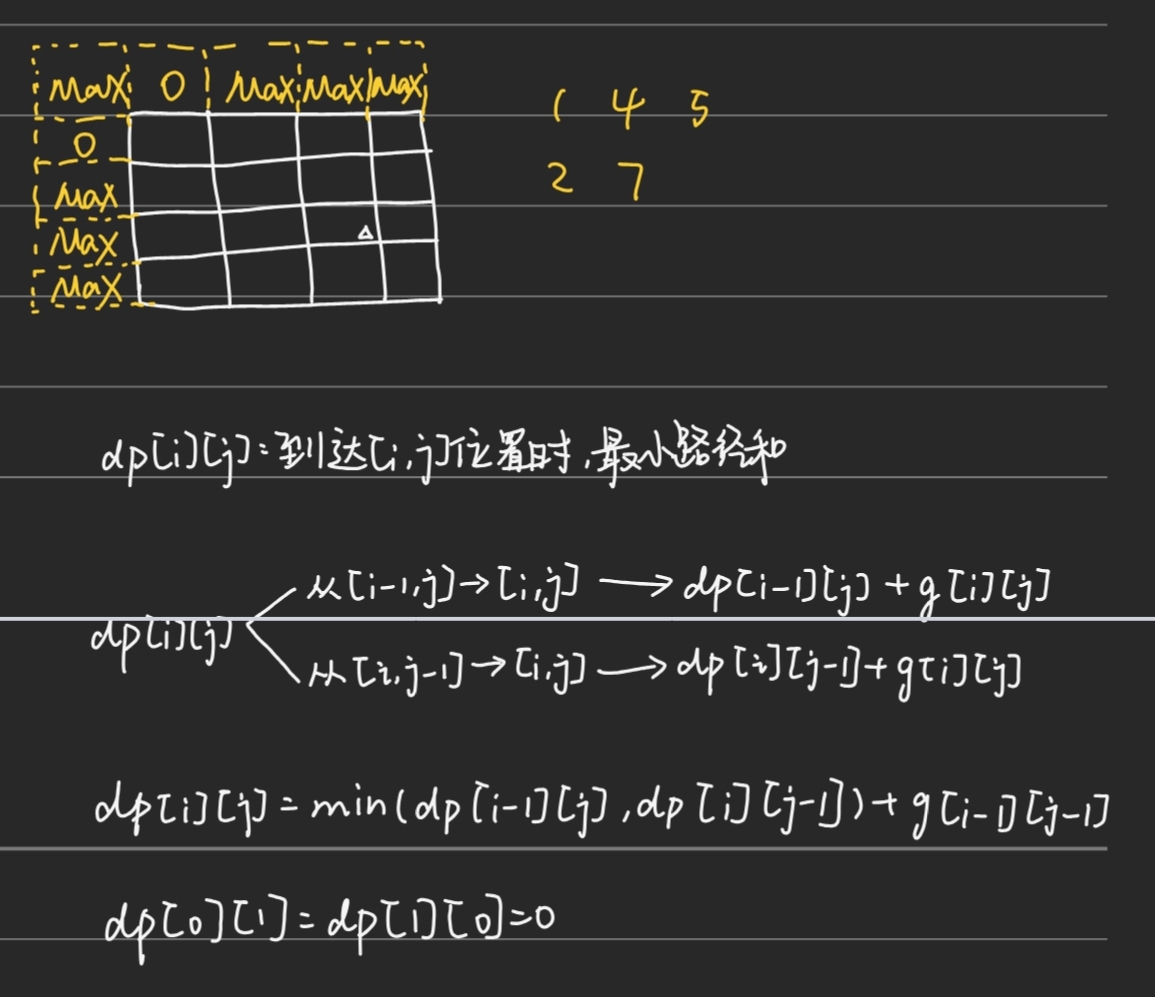
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m=grid.size(),n=grid[0].size();vector<vector<int>>dp(m+1,vector<int>(n+1,INT_MAX));dp[0][1]=dp[1][0]=0;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];}}return dp[m][n];}
};174. 地下城游戏


class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {int m=dungeon.size(),n=dungeon[0].size();vector<vector<int>>dp(m+1,vector<int>(n+1,INT_MAX));dp[m-1][n]=dp[m][n-1]=1;for(int i=m-1;i>=0;i--){for(int j=n-1;j>=0;j--){dp[i][j]=min(dp[i][j+1],dp[i+1][j])-dungeon[i][j];dp[i][j]=max(1,dp[i][j]);}}return dp[0][0];}
};三.简单多状态dp
⾯试题 17.16. 按摩师


class Solution {
public:int massage(vector<int>& nums) {int n=nums.size();if(n==0) return 0;vector<int>f(n);vector<int>g(n);f[0]=nums[0];g[0]=0;for(int i=1;i<n;i++){f[i]=g[i-1]+nums[i];g[i]=max(f[i-1],g[i-1]);}return max(f[n-1],g[n-1]);}
};213. 打家劫舍 II


class Solution {
public:int rob(vector<int>&nums){int n=nums.size();return max((nums[0]+rob1(nums,2,n-2)),rob1(nums,1,n-1));}int rob1(vector<int>& nums,int left,int right) {if(left>right) return 0;int n=nums.size();vector<int>f(n);vector<int>g(n);f[left]=nums[left];for(int i=left+1;i<=right;i++){f[i]=nums[i]+g[i-1];g[i]=max(g[i-1],f[i-1]);}return max(f[right],g[right]);}
};740. 删除并获得点数



class Solution {
public:int deleteAndEarn(vector<int>& nums) {const int N=10001;int arr[N]={0};//初始化很重要int n=nums.size();vector<int>f(N);auto g=f;for(int i=0;i<n;i++){arr[nums[i]]+=nums[i];}for(int i=1;i<N;i++){f[i]=arr[i]+g[i-1];g[i]=max(g[i-1],f[i-1]);}return max(f[N-1],g[N-1]);}
};剑指 Offer II 091. 粉刷房⼦

class Solution {
public:int minCost(vector<vector<int>>& costs) {int n=costs.size();vector<vector<int>>dp(n+1,vector<int>(3));for(int i=1;i<=n;i++){dp[i][1]=min(dp[i-1][0],dp[i-1][2])+costs[i-1][1];dp[i][0]=min(dp[i-1][1],dp[i-1][2])+costs[i-1][0];dp[i][2]=min(dp[i-1][0],dp[i-1][1])+costs[i-1][2];}return min(dp[n][0],min(dp[n][1],dp[n][2]));}
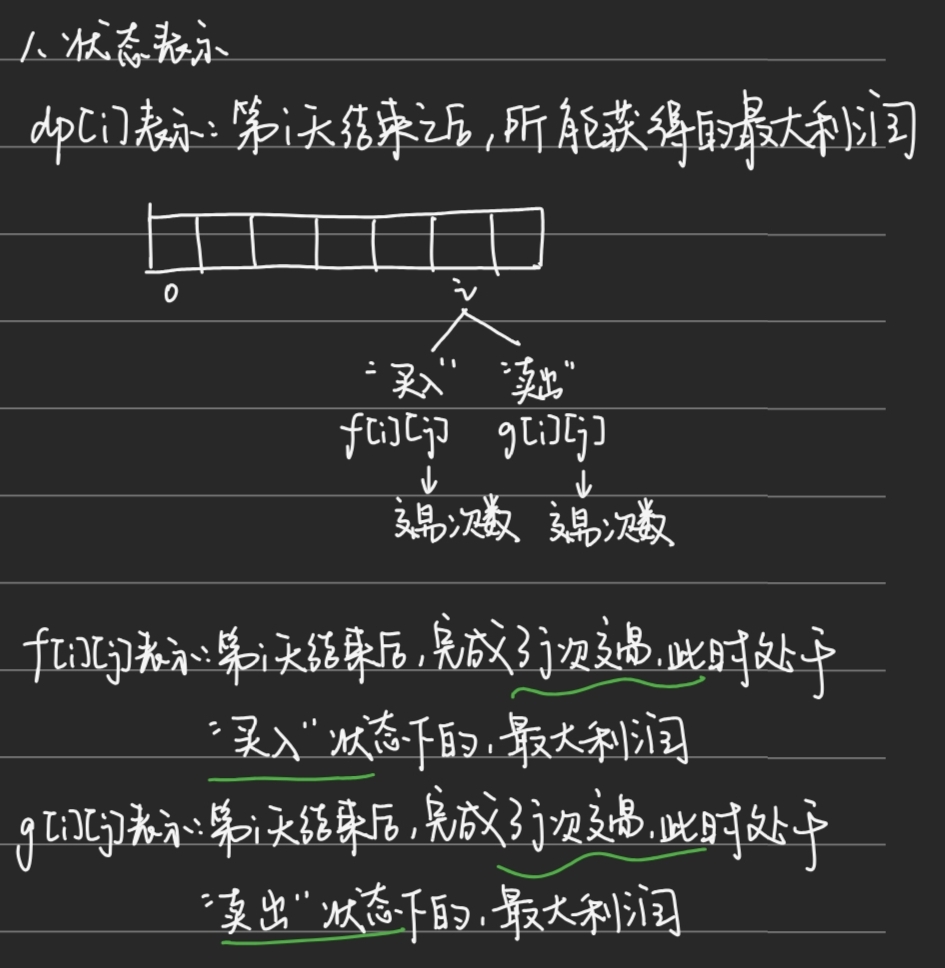
};309. 最佳买卖股票时机含冷冻期

class Solution {
public:int maxProfit(vector<int>& prices) {int n=prices.size();vector<vector<int>>dp(n,vector<int>(3));dp[0][0]=-prices[0];dp[0][1]=dp[0][2]=0;for(int i=1;i<n;i++){dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]);dp[i][1]=max(dp[i-1][1],dp[i-1][2]);dp[i][2]=dp[i-1][0]+prices[i];}return max(dp[n-1][1],dp[n-1][2]);//如果最后一天为买入状态,利润不可能最大}
};714. 买卖股票的最佳时机含⼿续费

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n=prices.size();vector<int>f(n);auto g=f;f[0]=-prices[0];g[0]=0;for(int i=1;i<n;i++){f[i]=max(f[i-1],g[i-1]-prices[i]);g[i]=max(f[i-1]+prices[i]-fee,g[i-1]);}return max(f[n-1],g[n-1]);}
};123. 买卖股票的最佳时机 III


class Solution {
public:int maxProfit(vector<int>& prices) {int n=prices.size();vector<vector<int>>f(n,vector<int>(3,-0x3f3f3f3f));auto g=f;f[0][0]=-prices[0];g[0][0]=0;int j=0;for(int i=1;i<n;i++){for(j=0;j<3;j++){f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);g[i][j]=g[i-1][j];if(j-1>=0)g[i][j]=max(f[i-1][j-1]+prices[i],g[i][j]);}}int mx=INT_MIN;for(int j=0;j<3;j++){mx=max(mx,g[n-1][j]);}return mx;}
};188. 买卖股票的最佳时机 IV

class Solution {
public:int maxProfit(int k, vector<int>& prices) {int n=prices.size();k=min(k,n/2);vector<vector<int>>f(n,vector<int>(k+1,-0x3f3f3f3f));auto g=f;f[0][0]=-prices[0];g[0][0]=0;int j=0;for(int i=1;i<n;i++){for(j=0;j<k+1;j++){f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);g[i][j]=g[i-1][j];if(j-1>=0)g[i][j]=max(f[i-1][j-1]+prices[i],g[i][j]);}}int mx=INT_MIN;for(int j=0;j<k+1;j++){mx=max(mx,g[n-1][j]);}return mx;}
};四.子数组系列(数组中连续的一段)
53. 最⼤⼦数组和


class Solution {
public:int maxSubArray(vector<int>& nums) {int n=nums.size();vector<int>dp(n);dp[0]=nums[0];for(int i=1;i<n;i++){dp[i]=max(nums[i],dp[i-1]+nums[i]);}int mx=INT_MIN;for(int i=0;i<n;i++){mx=max(mx,dp[i]);}return mx;}
};918. 环形⼦数组的最⼤和


class Solution {
public:int maxSubarraySumCircular(vector<int>& nums) {int n=nums.size();vector<int>f(n);int sum=0;for(auto&t:nums) sum+=t;auto g=f;f[0]=nums[0];g[0]=nums[0];for(int i=1;i<n;i++){f[i]=max(nums[i],f[i-1]+nums[i]);g[i]=min(nums[i],nums[i]+g[i-1]);}int mx=INT_MIN,mn=INT_MAX;for(int i=0;i<n;i++) mx=max(mx,f[i]);for(int i=0;i<n;i++) mn=min(mn,g[i]);return mn==sum?mx:max(mx,sum-mn);}
};152. 乘积最⼤⼦数组


class Solution {
public:int maxProduct(vector<int>& nums) {int n=nums.size();vector<int>f(n+1);auto g=f;f[0]=1;g[0]=1;for(int i=1;i<=n;i++){f[i]=max(nums[i-1]*g[i-1],max(nums[i-1],nums[i-1]*f[i-1]));g[i]=min(nums[i-1]*f[i-1],min(nums[i-1],nums[i-1]*g[i-1]));}int mx=INT_MIN;for(int i=1;i<=n;i++){mx=max(f[i],mx);}return mx;}}; 1567. 乘积为正数的最⻓⼦数组⻓度


class Solution {
public:int getMaxLen(vector<int>& nums) {int n=nums.size();vector<int>f(n+1);auto g=f;for(int i=1;i<=n;i++){if(nums[i-1]>0) {f[i]=f[i-1]+1;g[i]=(g[i-1]==0?0:g[i-1]+1);}if(nums[i-1]<0){f[i]=(g[i-1]==0?0:g[i-1]+1);g[i]=f[i-1]+1;}}int mx=INT_MIN;for(int i=1;i<=n;i++){mx=max(mx,f[i]);}return mx;}
};413. 等差数列划分

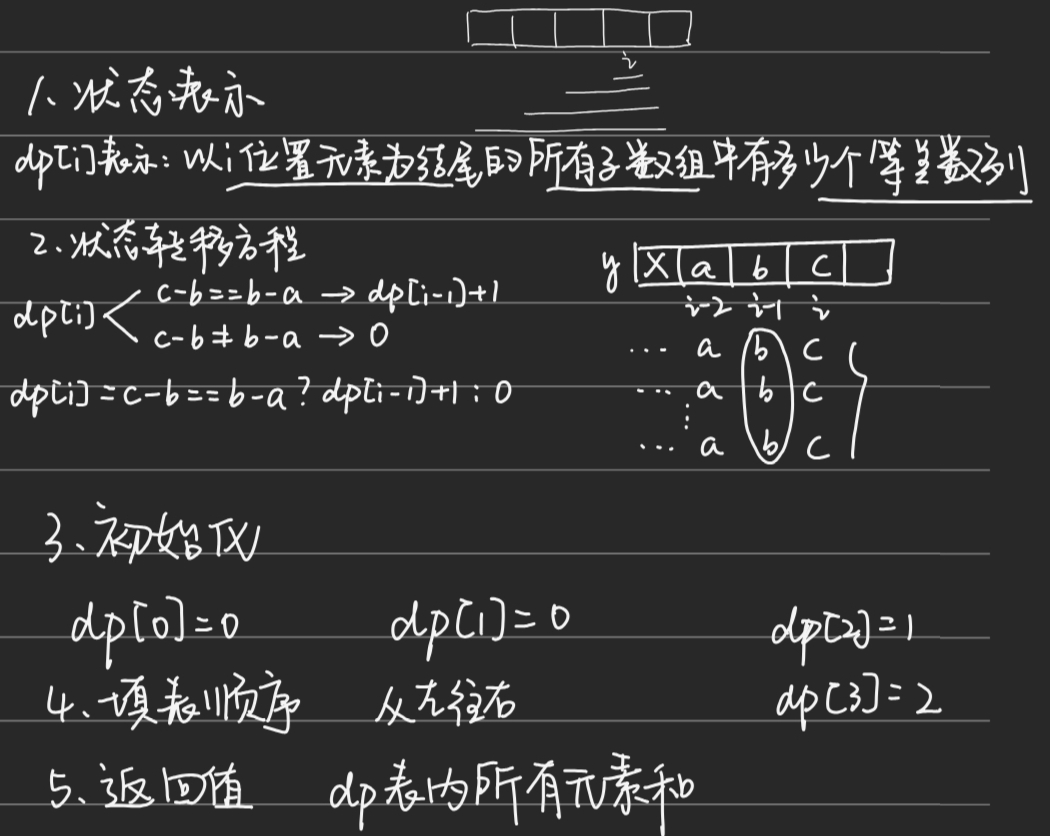
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n=nums.size();if(n<3) return 0;vector<int>dp(n);dp[0]=dp[1]=0;for(int i=2;i<n;i++){int a=nums[i-2];int b=nums[i-1];int c=nums[i];if(c-b==b-a) dp[i]=dp[i-1]+1;else dp[i]=0;}int sum=0;for(int i=2;i<n;i++) sum+=dp[i];return sum;}
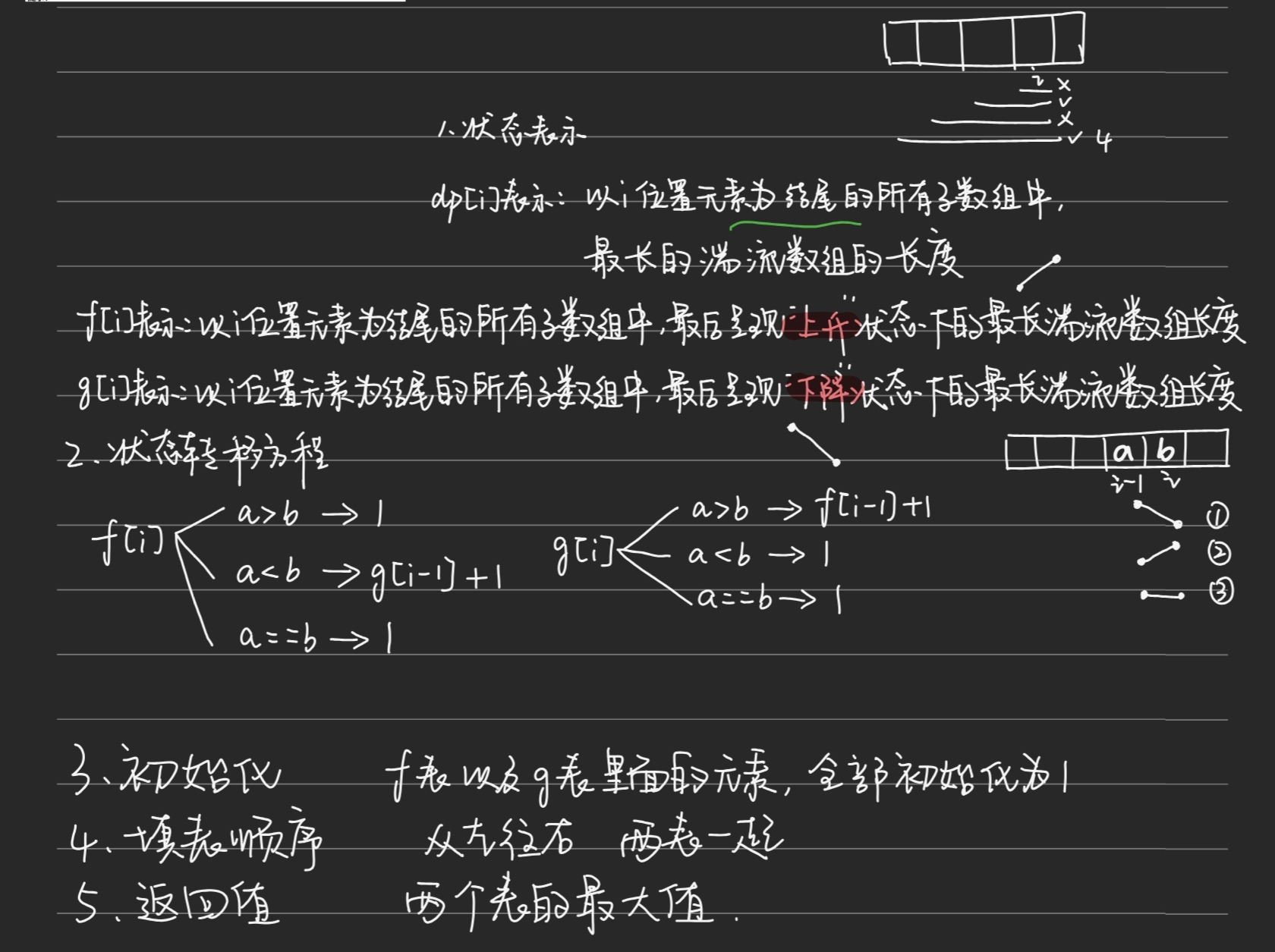
};978. 最⻓湍流⼦数组

class Solution {
public:int maxTurbulenceSize(vector<int>& arr) {int n = arr.size();vector<int> f(n, 1);auto g = f;for (int i = 1; i < n; i++) {int a = arr[i - 1];int b = arr[i];if (a > b) {f[i] = 1;g[i] = f[i - 1] + 1;} else if (a == b) {f[i] = 1;g[i] = 1;} else {f[i] = g[i - 1] + 1;g[i] = 1;}}int mx = INT_MIN;for (int i = 0; i < n; i++) {mx = max(max(f[i], g[i]), mx);}return mx;}
};139. 单词拆分


class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {int n=s.size();unordered_set<string> harsh(n+1);for(auto&t:wordDict) harsh.insert(t);vector<bool>dp(n+1);dp[0]=true;s=' '+s;for(int i=1;i<=n;i++){for(int j=i;j>=1;j--){if(dp[j-1]&&harsh.count(s.substr(j,i-j+1))){dp[i]=true;break;}}}return dp[n];}
};467. 环绕字符串中唯⼀的⼦字符串





class Solution {
public:int findSubstringInWraproundString(string s) {int n = s.size();// 1. 利⽤ dp 求出每个位置结尾的最⻓连续⼦数组的⻓度vector<int> dp(n, 1);for (int i = 1; i < n; i++)if (s[i] - 1 == s[i - 1] || (s[i - 1] == 'z' && s[i] == 'a'))dp[i] = dp[i - 1] + 1;// 2. 计算每⼀个字符结尾的最⻓连续⼦数组的⻓度int hash[26] = {0};for (int i = 0; i < n; i++)hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);// 3. 将结果累加起来int sum = 0;for (auto x : hash)sum += x;return sum;}
};五.子序列问题(数组中不连续的一段)
300. 最⻓递增⼦序列


class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n=nums.size();vector<int>dp(n,1);for(int i=1;i<n;i++){for(int j=0;j<i;j++){if(nums[i]>nums[j]){dp[i]=max(dp[i],dp[j]+1);//max更新dp[i]}}}int sum=1;for(auto&e:dp){sum=max(sum,e);}return sum;}
};376. 摆动序列


class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n=nums.size();vector<int>f(n,1);auto g=f;for(int i=1;i<n;i++){for(int j=0;j<i;j++){if(nums[i]>nums[j]){f[i]=max(f[i],g[j]+1);}else if(nums[i]<nums[j]){g[i]=max(g[i],f[j]+1);}}}int ret=0;for(int i=0;i<n;i++){ret=max(ret,max(f[i],g[i]));}return ret;}
};673. 最⻓递增⼦序列的个数


class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> len(n, 1), count(n, 1);int Len = len[0];int Count = count[0];for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (nums[j] < nums[i]) {if (len[j] + 1 == len[i]) {count[i] += count[j];} else if (len[j] + 1 > len[i]) {len[i] = len[j] + 1;count[i] = count[j];}}}if (len[i] > Len) {Len = len[i];Count = count[i];} else if (len[i] == Len) {Count += count[i];}}return Count;}
};646. 最⻓数对链

class Solution {
public:int findLongestChain(vector<vector<int>>& pairs) {sort(pairs.begin(),pairs.end());int n=pairs.size();vector<int> dp(n,1);for(int i=1;i<n;i++){for(int j=0;j<i;j++){if(pairs[j][1]<pairs[i][0]){dp[i]=max(dp[i],dp[j]+1);}}}int ret=0;for(int i=0;i<n;i++){ret=max(ret,dp[i]);}return ret;}
};1218. 最⻓定差⼦序列
class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {unordered_map<int,int> hash;hash[arr[0]]=1;int ret=1;for(int i=1;i<arr.size();i++){hash[arr[i]]=hash[arr[i]-difference]+1;ret=max(hash[arr[i]],ret);}return ret;}
};873. 最⻓的斐波那契⼦序列的⻓度()

class Solution {
public:int lenLongestFibSubseq(vector<int>& arr) {int n=arr.size();unordered_map<int,int> hash(n);vector<vector<int>> dp(n,vector<int>(n,2));for(int i=0;i<n;i++) hash[arr[i]]=i;//存放对应下标int ret=2;for(int j=2;j<n;j++){for(int i=1;i<n;i++){int k=arr[j]-arr[i];if(k<arr[i]&&hash[k])dp[i][j]=dp[hash[k]][i]+1;ret=max(ret,dp[i][j]);}}return ret<3?0:ret;//2个及以下构成不了斐波那契数列}
};1027. 最⻓等差数列()

446. 等差数列划分 II - ⼦序列()

class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();// 优化unordered_map<long long, vector<int>> hash;for (int i = 0; i < n; i++)hash[nums[i]].push_back(i);vector<vector<int>> dp(n, vector<int>(n)); // 创建 dp 表int sum = 0;for (int j = 2; j < n; j++) // 固定倒数第⼀个数{for (int i = 1; i < j; i++) // 枚举倒数第⼆个数{long long a = (long long)nums[i] * 2 - nums[j]; // 处理数据溢出if (hash.count(a))for (auto k : hash[a])if (k < i)dp[i][j] += dp[k][i] + 1;elsebreak;sum += dp[i][j];}}return sum;}
};六.回文串问题
647. 回⽂⼦串


class Solution {
public:int countSubstrings(string s) {int n=s.size();vector<vector<bool>>dp (n,vector<bool>(n));int sum=0;for(int i=n-1;i>=0;i--){for(int j=i;j<n;j++){if(s[i]==s[j])dp[i][j]=i+1<j?dp[i+1][j-1]:true;if(dp[i][j])sum+=1;}}return sum;}
};5. 最⻓回⽂⼦串

class Solution {
public:string longestPalindrome(string s) {int len = 1;//更新begin和endint n = s.size();int begin=0,end = 0;vector<vector<bool>>dp(n,vector<bool>(n));for (int i = 0; i <=n-1; i++) {for (int j = i; j >=0; j--) {if (s[i] == s[j])dp[i][j] = j + 1 < i ? dp[i - 1][j + 1] : true;if (dp[i][j] && i-j + 1 > len) {len = i-j + 1;begin=j;end=i;}}}return s.substr(begin,len); }
};1745. 回⽂串分割 IV


class Solution {
public:bool checkPartitioning(string s) {int n=s.size();vector<vector<bool>>dp(n,vector<bool>(n));for(int i=n-1;i>=0;i--){for(int j=i;j<n;j++){if(s[i]==s[j])dp[i][j]=i+1<j?dp[i+1][j-1]:true;}}for(int i=1;i<n;i++){for(int j=i;j<n-1;j++){if(dp[0][i-1]&&dp[i][j]&&dp[j+1][n-1])return true;}}return false;}
};132. 分割回⽂串 II

class Solution {
public:int minCut(string s) {int n=s.size();vector<vector<bool>>ispal(n,vector<bool>(n,false));for(int i=n-1;i>=0;i--){for(int j=i;j<n;j++){if(s[i]==s[j])ispal[i][j]=i+1<j?ispal[i+1][j-1]:true;}}vector<int>dp(n,INT_MAX);for(int i=0;i<n;i++){if(ispal[0][i]) dp[i]=0;else{for(int j=1;j<=i;j++){if(ispal[j][i])dp[i]=min(dp[i],dp[j-1]+1);}}}return dp[n-1];}
};516. 最⻓回⽂⼦序列

class Solution {
public:int longestPalindromeSubseq(string s) {int n=s.size();vector<vector<int>>dp(n,vector<int>(n));for(int i=n-1;i>=0;i--){dp[i][i]=1; for(int j=i+1;j<n;j++){if(s[i]==s[j]){dp[i][j]=dp[i+1][j-1]+2;}else{dp[i][j]=max(dp[i][j-1],dp[i+1][j]);}}}return dp[0][n-1];}
};1312. 让字符串成为回⽂串的最少插⼊次数

class Solution {
public:int minInsertions(string s) {int n=s.size();vector<vector<int>>dp(n,vector<int>(n));for(int i=n-1;i>=0;i--){for(int j=i+1;j<n;j++){if(s[i]==s[j]) {if(i+1<j)dp[i][j]=dp[i+1][j-1];}else{dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1;}}}return dp[0][n-1];}
};七.两个数组的dp问题(含字符串数组)
1143. 最⻓公共⼦序列


class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int s1 = text1.size();int s2 = text2.size();vector<vector<int>> dp(s1 + 1, vector<int>(s2 + 1));text1 = " " + text1;text2 = " " + text2;for (int i = 1; i <= s1; i++) {for (int j = 1; j <= s2; j++) {if (text1[i] == text2[j])dp[i][j] = dp[i - 1][j - 1] + 1;elsedp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}return dp[s1][s2];}
};1035. 不相交的线


class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {int m=nums1.size();int n=nums2.size();vector<vector<int>>dp(m+1,vector<int>(n+1));for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}return dp[m][n];}
};115. 不同的⼦序列

class Solution {
public:int numDistinct(string s, string t) {int m=t.size();int n=s.size();vector<vector<int>>dp(m+1,vector<int>(n+1));for(int i=0;i<=n;i++) dp[0][i]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=(dp[i][j]+dp[i][j-1])%1000000007;if(t[i-1]==s[j-1])dp[i][j]=(dp[i][j]+dp[i-1][j-1])%1000000007;}}return dp[m][n];}
};44. 通配符匹配()

class Solution {
public:bool isMatch(string s, string p) {int m = s.size(), n = p.size();s = " " + s, p = " " + p;// 1. 创建 dp 表// 2. 初始化dp[0][0] = true; vector<vector<bool>> dp(m + 1, vector<bool>(n + 1)); for (int j = 1; j <= n; j++)if (p[j] == '*')dp[0][j] = true;elsebreak;// 3. 填表for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (p[j] == '*')dp[i][j] = dp[i - 1][j] || dp[i][j - 1];elsedp[i][j] =(p[j] == '?' || s[i] == p[j]) && dp[i - 1][j - 1];}}// 4. 返回值return dp[m][n];}
};10. 正则表达式匹配()

class Solution {
public:bool isMatch(string s, string p) {int m = s.size();int n = p.size();vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));dp[0][0] = true;s = ' ' + s;p = ' ' + p;for (int i = 2; i <= n; i += 2) {if (p[i] == '*')dp[0][i] = true;elsebreak;}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (p[j] == '*')dp[i][j] =dp[i][j - 2] ||(p[j - 1] == '.' || p[j - 1] == s[i]) && dp[i - 1][j];elsedp[i][j] =(p[j] == '.' || p[j] == s[i]) && dp[i - 1][j - 1];}}return dp[m][n];}
};97. 交错字符串


class Solution {
public:bool isInterleave(string s1, string s2, string s3) {int m=s1.size();int n=s2.size();int q=s3.size();s1=' '+s1;s2=' '+s2;s3=' '+s3;vector<vector<bool>>dp(m+1,vector<bool>(n+1));if(m+n!=q) return false;//s1=" s2=" " s3=" "a"dp[0][0]=true;for(int i=1;i<=n;i++){if(s2[i]==s3[i]) dp[0][i]=true;else break;}for(int i=1;i<=m;i++){if(s1[i]==s3[i]) dp[i][0]=true;else break;}for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){if((s1[i]==s3[i+j]&&dp[i-1][j])||s2[j]==s3[i+j]&&dp[i][j-1]) dp[i][j]=true;}}return dp[m][n];}
};712. 两个字符串的最⼩ASCII删除和

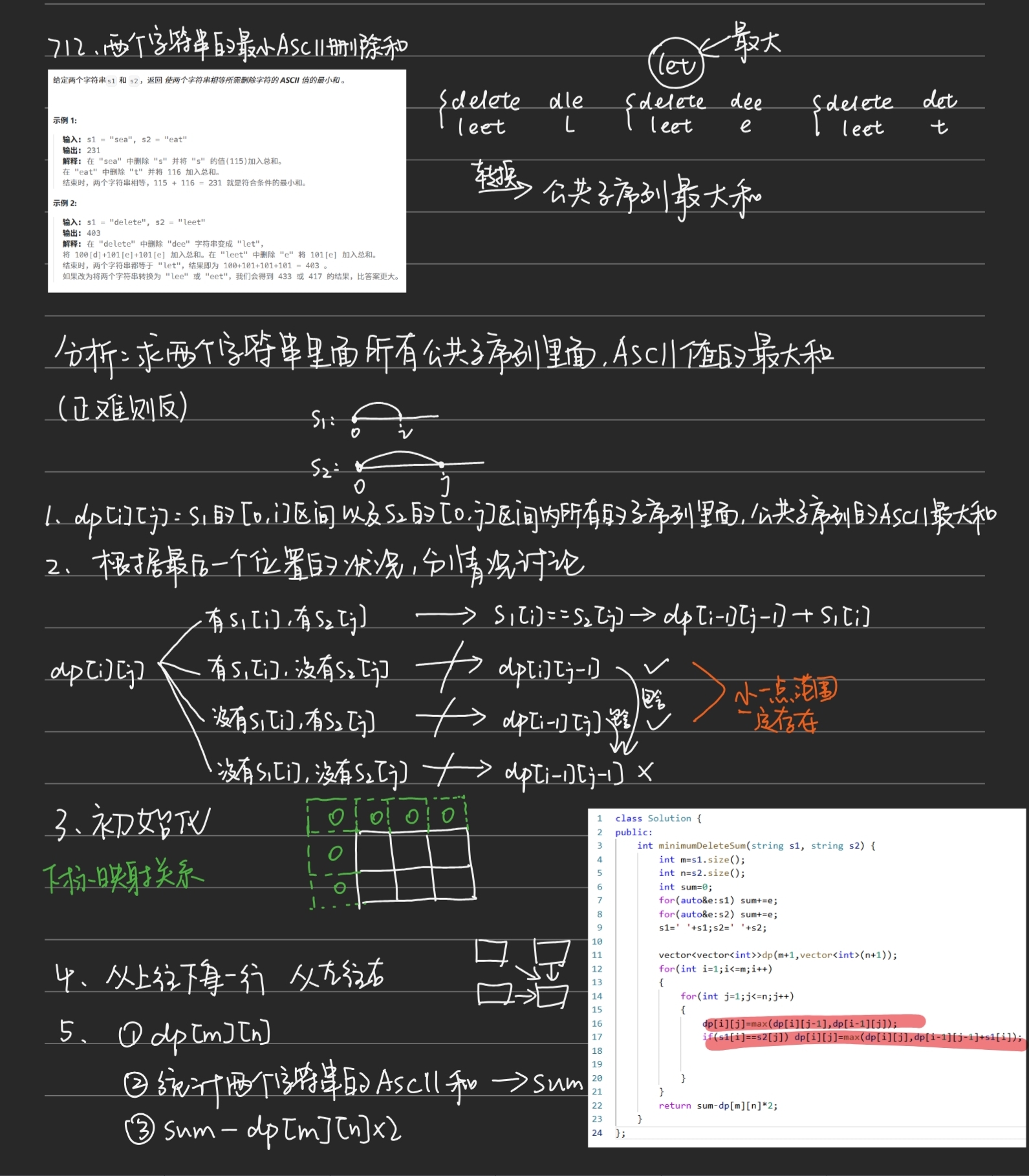
class Solution {
public:int minimumDeleteSum(string s1, string s2) {int m=s1.size();int n=s2.size();int sum=0;for(auto&e:s1) sum+=e;for(auto&e:s2) sum+=e;s1=' '+s1;s2=' '+s2;vector<vector<int>>dp(m+1,vector<int>(n+1));for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=max(dp[i][j-1],dp[i-1][j]);if(s1[i]==s2[j]) dp[i][j]=max(dp[i][j],dp[i-1][j-1]+s1[i]);}}return sum-dp[m][n]*2;}
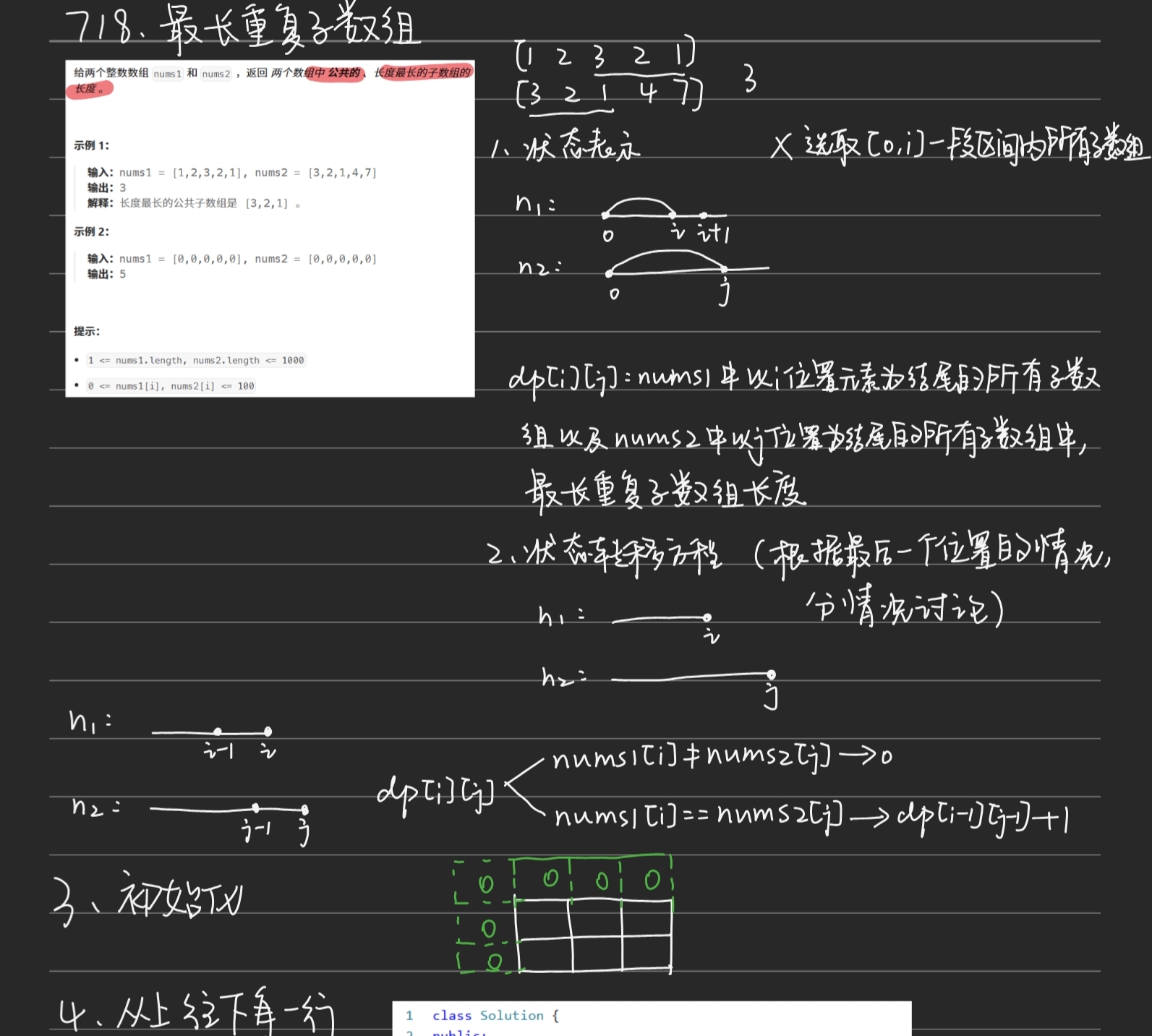
}; 718. 最⻓重复⼦数组
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int m=nums1.size();int n=nums2.size();int ret=0;vector<vector<int>>dp(m+1,vector<int>(n+1));for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){if(nums1[i-1]!=nums2[j-1]) dp[i][j]=0;else dp[i][j]=dp[i-1][j-1]+1;ret=max(ret,dp[i][j]);}}return ret;}
};八.01背包问题
DP41 【模板】01背包
1.最大的价值
2.装满时的最大价值

#include <iostream>
#include<cstring>
#include<vector>
using namespace std;
int main() {int n,V;cin>>n>>V;vector<int>w(n);vector<int>v(n);vector<vector<int>>dp(n+1,vector<int>(V+1,0));for(int i=0;i<n;i++){cin>>w[i]>>v[i];}for(int i=1;i<=n;i++){for(int j=0;j<=V;j++){dp[i][j]=dp[i-1][j];if(j>=w[i-1]) dp[i][j]=max(dp[i][j],dp[i-1][j-w[i-1]]+v[i-1]);}}cout<<dp[n][V]<<endl;for (auto &row : dp) std::fill(row.begin(), row.end(), 0);for(int i=1;i<=V;i++) dp[0][i]=-1;for(int i=1;i<=n;i++){for(int j=0;j<=V;j++){dp[i][j]=dp[i-1][j];if(j>=w[i-1]&&dp[i-1][j-w[i-1]]!=-1) dp[i][j]=max(dp[i][j],dp[i-1][j-w[i-1]]+v[i-1]);}}cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;
}优化:
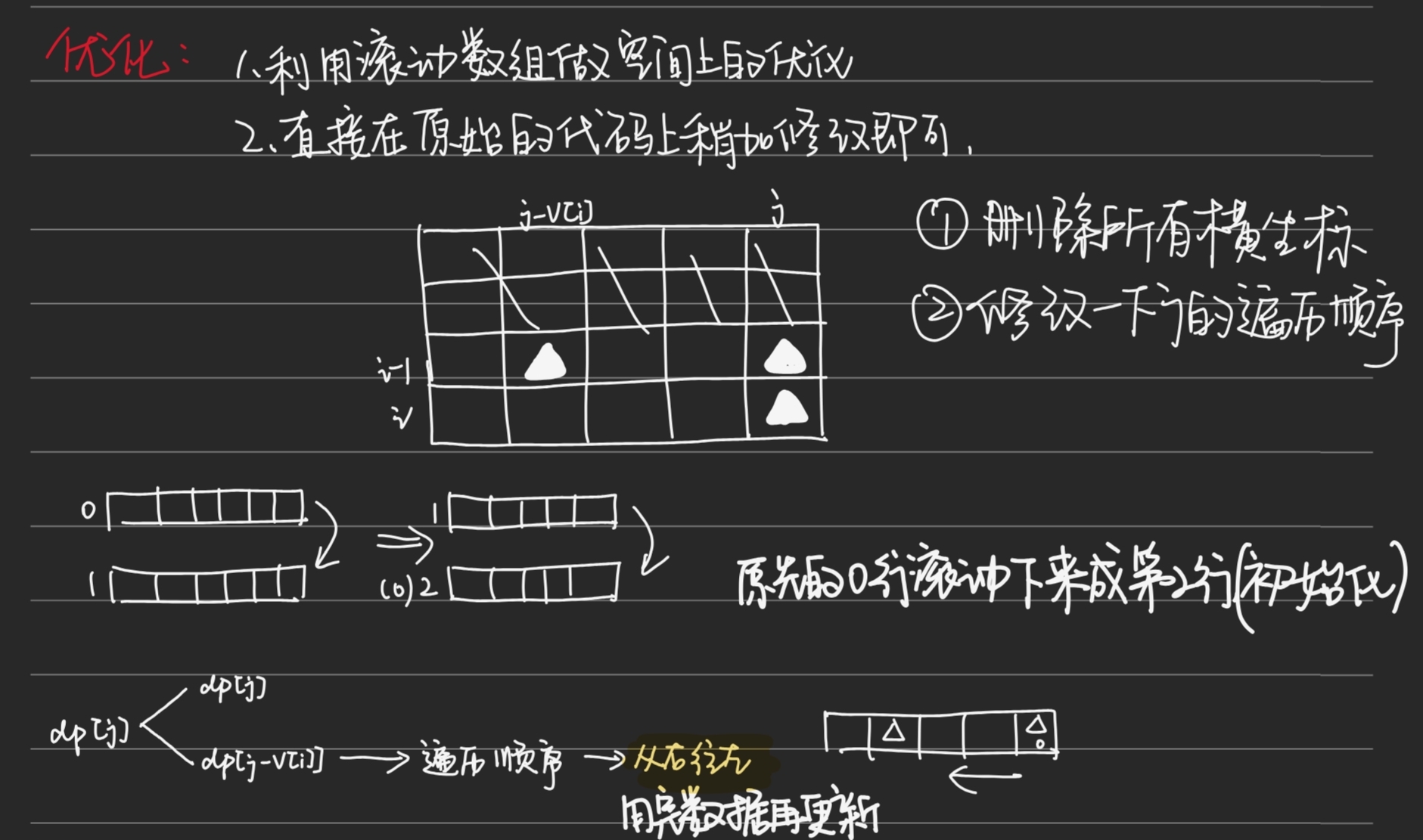
#include <iostream>
#include<cstring>
#include<vector>
using namespace std;
int main() {int n,V;cin>>n>>V;vector<int>w(n);vector<int>v(n);vector<int>dp(V+1,0);for(int i=0;i<n;i++){cin>>w[i]>>v[i];}for(int i=1;i<=n;i++){for(int j=V;j>=w[i-1];j--){dp[j]=max(dp[j],v[i-1]+dp[j-w[i-1]]);}}cout<<dp[V]<<endl;std::fill(dp.begin(),dp.end(),0);for(int i=1;i<=V;i++) dp[i]=-1;for(int i=1;i<=n;i++){for(int j=V;j>=w[i-1];j--){if(dp[j-w[i-1]]!=-1) dp[j]=max(dp[j],dp[j-w[i-1]]+v[i-1]);}}cout<<(dp[V]==-1?0:dp[V])<<endl;
}416. 分割等和子集

class Solution {
public:bool canPartition(vector<int>& nums) {int n=nums.size();int sum=0;for(auto&e:nums) sum+=e;if(sum%2==1) return false;int s=sum/2;vector<vector<bool>>dp(n+1,vector<bool>(s+1));for(int i=0;i<=n;i++) dp[i][0]=true;for(int i=1;i<=n;i++){for(int j=1;j<=s;j++){dp[i][j]=dp[i-1][j];if(j>=nums[i-1]) dp[i][j]=dp[i][j]||dp[i-1][j-nums[i-1]];}}return dp[n][s];}
};494. ⽬标和(装满背包的选法)

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum=0;for(auto&item:nums) sum+=item;int n=nums.size();int a=(sum+target)/2;if(a<0||(sum+target)%2==1) return 0;vector<vector<int>>dp(n+1,vector<int>(a+1));dp[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=a;j++){dp[i][j]=dp[i-1][j];if(j>=nums[i-1]) dp[i][j]+=dp[i-1][j-nums[i-1]];}}return dp[n][a];}
};1049. 最后⼀块⽯头的重量 II

class Solution {
public:int lastStoneWeightII(vector<int>& nums) {int n=nums.size();int sum=0;for(auto&e:nums) sum+=e;int a=sum/2;vector<vector<int>>dp(n+1,vector<int>(a+1));for(int i=1;i<=n;i++){for(int j=0;j<=a;j++){dp[i][j]=dp[i-1][j];if(j>=nums[i-1]) dp[i][j]=max(dp[i][j],nums[i-1]+dp[i-1][j-nums[i-1]]);}}return sum-2*dp[n][a];}
};九.完全背包问题
DP42 【模板】完全背包
1.最大的价值
2.背包装满的最大价值

#include <iostream>
#include<cstring>
using namespace std;
#include<vector>
int main() {int n,V;cin>>n>>V;vector<int>v(n);vector<int>w(n);vector<vector<int>>dp(n+1,vector<int>(V+1,0));for(int i=0;i<n;i++) cin>>w[i]>>v[i];for(int i=1;i<=n;i++){for(int j=0;j<=V;j++){dp[i][j]=dp[i-1][j];if(j>=w[i-1]) dp[i][j]=max(dp[i][j],v[i-1]+dp[i][j-w[i-1]]);}}cout<<dp[n][V]<<endl;for (auto &row : dp) std::fill(row.begin(), row.end(), 0);for(int i=1;i<=V;i++) dp[0][i]=-1;for(int i=1;i<=n;i++){for(int j=0;j<=V;j++){dp[i][j]=dp[i-1][j];if(j>=w[i-1]&&dp[i][j-w[i-1]]!=-1) dp[i][j]=max(dp[i][j],v[i-1]+dp[i][j-w[i-1]]);}}cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;
}
// 64 位输出请用 printf("%lld")322. 零钱兑换

class Solution {
public:int coinChange(vector<int>& coins, int amount) {int n=coins.size();vector<vector<int>>dp(n+1,vector<int>(amount+1));for(int i=1;i<=amount;i++) dp[0][i]=0x3f3f3f3f;for(int i=1;i<=n;i++){for(int j=0;j<=amount;j++){dp[i][j]=dp[i-1][j];if(j>=coins[i-1]) dp[i][j]=min(dp[i][j],dp[i][j-coins[i-1]]+1);}}return (dp[n][amount]>=0x3f3f3f3f)?-1:dp[n][amount];}
};518. 零钱兑换 II


class Solution {
public:int change(int amount, vector<int>& coins) {int n=coins.size();const int MOD=1e10+7;vector<vector<long long>>dp(n+1,vector<long long>(amount+1,0));dp[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=amount;j++){dp[i][j]=dp[i-1][j];if(j>=coins[i-1]) dp[i][j]=(dp[i][j]+dp[i][j-coins[i-1]])%MOD;}}return dp[n][amount];}
};279. 完全平⽅数

class Solution {
public:int numSquares(int n) {int m=sqrt(n);//开根vector<vector<long long>>dp(m+1,vector<long long>(n+1));const int INF=0x3f3f3f3f;for(int i=1;i<=n;i++) dp[0][i]=INF;for(int i=1;i<=m;i++){for(int j=0;j<=n;j++){dp[i][j]=dp[i-1][j];if(j>=i*i)dp[i][j]=min(dp[i][j],dp[i][j-i*i]+1);}}return dp[m][n];}};










)



