【算法】（Python）分治算法

分治算法：

分而治之。
将一个问题分成若干个子问题（甚至更小的子子问题），子问题相互独立、与原问题性质相同。
子问题的解可以合并得到原问题的解。
应用：二分查找、归并排序、快速排序等。
步骤：① 将问题分成多个同类子问题，② 求解子问题，③ 将子问题的解逐层合并获得原问题的解。

1、（难度：简单）【力扣】LCR 161. 连续天数的最高销售额

解题思路：将数组从中间拆分左右两部分，直到拆分成一个一个的元素，再逐层合并左右两部分，获取四个数据的最大和。最终返回中间部分最大和。

四个数据的最大和：

左侧最大和：左侧第一个元素开始往右的最大和。涉及2个情况：左子区间的左侧最大和、左子区间的总和+右子区间的左侧最大和，取最大值。
右侧最大和：右侧第一个元素开始往左的最大和。涉及2个情况：右子区间的右侧最大和、右子区间的总和+左子区间的右侧最大和，取最大值。
中间最大和：中间位置的最大和。涉及3个情况：左子区间的中间最大和、右子区间的中间最大和、左子区间的右侧最大和+右子区间的左侧最大和，取最大值。
区间总和：整个区间的和。包括左子区间的总和、右子区间的总和。

时间复杂度：O(n)。空间复杂度：O(logn)。

class Solution:def maxSales(self, sales: List[int]) -> int:def func(left:int, right:int):# 终止条件：拆分到只剩一个元素，返回if left == right:# 返回左侧最大和、右侧最大和、中间最大和、区间总和（均为该元素）return [sales[left]] * 4# 从中间拆分成左右子区间mid = (left + right) >> 1l_lsum, l_rsum, l_msum, l_isum = func(left, mid)r_lsum, r_rsum, r_msum, r_isum = func(mid + 1, right)# 合并左右子区间# 从左侧开始的最大和：# max(左子区间的左侧最大和, 左子区间的区间总和+右子区间的左侧最大和)lsum = max(l_lsum, l_isum + r_lsum)# 从右侧开始的最大和：# max(右子区间的右侧最大和, 右子区间的区间总和+左子区间的右侧最大和)rsum = max(r_rsum, r_isum + l_rsum)# 中间的最大和：# max(max(左子区间的中间最大和,右子区间的中间最大和), 左子区间的右侧最大和+右子区间的左侧最大和)msum = max(max(l_msum, r_msum), l_rsum + r_lsum)# 区间总和：# 左子区间的区间总和+右子区间的区间总和isum = l_isum + r_isum# 返回左侧最大和、右侧最大和、中间最大和、区间总和return [lsum, rsum, msum, isum]# 返回最终中间最大和return func(0, len(sales) - 1)[2]

使用面向对象（创建类），类中包括四个数据。

# 类foursum
class foursum:def __init__(self, lsum, rsum, msum, isum):self.lsum = lsum         # 从左侧开始的最大和self.rsum = rsum         # 从右侧开始的最大和self.msum = msum         # 中间的最大和self.isum = isum         # 区间总和class Solution:def maxSales(self, sales: List[int]) -> int:# 合并左右子区间def mergemax(l:foursum, r:foursum):lsum = max(l.lsum, l.isum + r.lsum)rsum = max(r.rsum, r.isum + l.rsum)msum = max(max(l.msum, r.msum), l.rsum + r.lsum)isum = l.isum + r.isum# 返回：类实例(左侧最大和、右侧最大和、中间最大和、区间总和)return foursum(lsum, rsum, msum, isum)# 获取最大和def get(left:int, right:int):# 终止条件：拆分到只剩一个元素，返回if left == right:return foursum(sales[left], sales[left], sales[left], sales[left])# 从中间拆分成左右子区间mid = (left + right) >> 1lsub = get(left, mid)rsub = get(mid + 1, right)# 返回合并左右子区间后的结果return mergemax(lsub, rsub)# 返回最终中间最大和return get(0, (len(sales) - 1)).msum

注：本题其他解决方法：动态规划。本文忽略。

2、（难度：中等）【力扣】109. 有序链表转换二叉搜索树

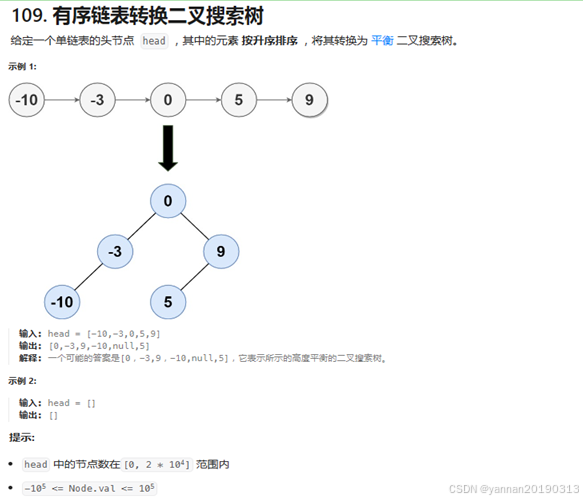
平衡二叉搜索树：

各节点的左子树都比该节点数值小，右子树都比该节点数值大。

各节点的左子树和右子树的高度差最多为1。

解题思路：从链表中间位置，逐次拆分成左右两部分（相当于左右子树），再逐层构建平衡二叉搜索树。

（本处中位数为：总个数为奇数，中位数为中间的数。总个数为偶数，中位数为中间2个数中的后面那个数）

本题有两种方法：

① 使用快慢指针找到中位数，逐次拆分递归构建左右子树，
② 获取链表总个数，通过计算找到中位数，使用中序遍历方式递归构建平衡二叉搜索树。

方法 ①：

注意：快慢指针起始都指向链表左端点。慢指针走1步，快指针走2步，快指针走完，慢指针到达中位数的位置。

链表总个数有奇偶，慢指针到达中位数时，快指针指向位置有两种情况，

链表总个数为奇数时，快指针到右端点的最后那个节点（fast.next=None），
链表总个数为偶数时，快指针到右端点后的空节点（fast=None）。

时间复杂度：O(nlogn)。空间复杂度：O(logn)。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:# 查找中位数def getmid(left:ListNode, right:ListNode):# 快慢指针，初始都指向链表左端点slow, fast = left, left# 快指针走2步，慢指针走1步，快指针到右端点(总个数分奇偶)，则慢指针指向的是中位数while fast != right and fast.next != right:slow = slow.nextfast = fast.next.next# 返回慢指针return slow# 转换为平衡二叉搜索树def buildtree(left:ListNode, right:ListNode):# 终止条件if left == right: return# 获取中位数mid = getmid(left, right)# 根节点为中位数的内容root = TreeNode(mid.val)# 左子节点root.left = buildtree(left, mid)# 右子节点root.right = buildtree(mid.next, right)# 返回节点return root# 返回最终的平衡二叉搜索树return buildtree(head, None)

方法 ②：

注意：左右边界是否包含。本方法左右边界均包含在范围内。左边界left起始为0，右边界right起始为链表长度-1，中位数mid为（左边界+右边界+1）除以2取整。

时间复杂度：O(n)。空间复杂度：O(logn)。

知识点：a >> 1：数值a二进制左移1位，即a//2，a除以2取整。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:# 获取链表长度，（用于获取中位数）def getlen(head:ListNode):n = 0while head:head = head.nextn += 1return n# 转换为平衡二叉搜索树def buildtree(left:int, right:int):# 终止条件if left > right: return# 获取中位数mid = (left + right + 1) >> 1# 使用中序遍历构建树# 左子节点node = TreeNode()node.left = buildtree(left, mid - 1)# 根节点nonlocal headnode.val = head.valhead = head.next# 右子节点node.right = buildtree(mid + 1, right)# 返回节点return node# 获取链表长度n = getlen(head)# 返回最终的平衡二叉搜索树return buildtree(0, n - 1)

3、（难度：困难）【力扣】315. 计算右侧小于当前元素的个数

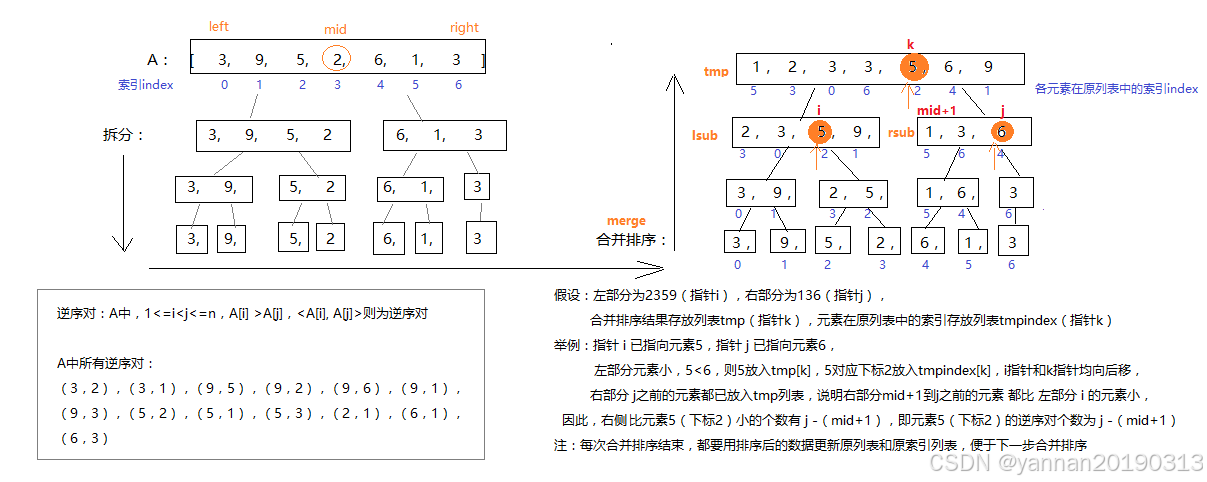
解题思路：从数组中间位置，逐步拆分成左右两部分，直到一个一个的元素，再逐层将左右两部分按从小到大顺序合并排列。合并结果存放到临时列表tmp中，各元素对应的下标存放到临时索引列表tmpindex中，统计逆序对（右侧元素比左侧元素小）的个数。

注意：

记录合并排序结果和元素对应的下标，可用元组形式，即（元素，下标）。本文使用两个列表tmp和tmpindex分别记录。
本文使用的方法中，每次合并排序后，都要用排序后的结果tmp和对应的下标tmpindex更新原列表nums和对应的索引列表index，便于下一轮合并排序。

时间复杂度：O(nlogn)。空间复杂度：O(n)。

知识点：逆序对：数学术语。数组A，正整数i,j，使得 1 $\leq$ i < j $\leq$ n 且 A(i) > A(j)，则<A(i), A(j)>为逆序对。

class Solution:def countSmaller(self, nums: List[int]) -> List[int]:# 归并排序def mergesort(left:int, right:int):# 终止条件if left >= right: return# 获取中间数mid = (left + right) >> 1# 拆分为左右两部分mergesort(left, mid)mergesort(mid + 1, right)# 合并左右两部分merge(left, mid, right)# # 合并左右两部分def merge(left:int, mid:int, right:int):# 两个指针，初始分别指向左部分和右部分第一个元素i, j = left, mid + 1# 指向tmp列表中元素的指针k = left# 左右两部分都有元素，数值小的记录到tmp列表，对应下标记录到tmpindex列表while i <= mid and j <= right:# 若右部分的元素小if nums[i] > nums[j]: tmp[k] = nums[j]         # 较小的元素 存入tmptmpindex[k] = index[j]   # 较小的元素的下标 存入tmpindexk += 1j += 1# 若左部分的元素小else: tmp[k] = nums[i]         # 较小的元素 存入tmptmpindex[k] = index[i]   # 较小的元素的下标 存入tmpindex# 记录逆序对，右部分j之前的元素都小于左部分i的元素counts[index[i]] += (j- mid - 1)k += 1                    i += 1# 右部分遍历完。左部分仍有元素，添加到tmp列表while i <= mid:tmp[k] = nums[i]         # 较小的元素 存入tmptmpindex[k] = index[i]   # 较小的元素的下标 存入tmpindex# 记录逆序对，右部分j之前的元素都小于左部分i的元素counts[index[i]] += (j- mid - 1)k += 1                    i += 1# 左部分遍历完。右部分仍有元素，添加到tmp列表while j <= right:tmp[k] = nums[j]         # 较小的元素 存入tmptmpindex[k] = index[j]   # 较小的元素的下标 存入tmpindexk += 1j += 1# 排序后的tmp列表中数据更新nums，tmpindex列表中数据更新indexfor x in range(left, right + 1):# 合并排序后的各元素下标，用于下一轮合并排序index[x] = tmpindex[x]nums[x] = tmp[x]n = len(nums)# 记录各元素右侧小于它的个数，初始都为0counts = [0] * n# 索引列表，记录各元素在初始nums列表中对应的下标位置index = [i for i in range(len(nums))]# 左右部分合并排序时，记录从小到大排列结果tmp = [0] * n# 左右两部分合并排序时，记录tmp中各元素对应的下标位置tmpindex = [0] * n# 执行归并排序mergesort(0, n - 1) return counts

本题还有其他的解题办法：离散化树状数组，本文忽略。原始办法：两重循环进行枚举。

【算法】（Python）分治算法

相关资讯

热文排行

最新新闻

推荐新闻

热搜词