文章目录
- 1. 图(Graphs)
- 1.1 边(Edge)的类型
- 1.2 图的类型
- 1.3 其他基本术语
- 1.4 子图(Subgraph)
- 1.5 树(Tree)
- 1.5.1 树的性质
- 1.5.2 生成树(Spanning Tree)和生成森林(Spanning Forest)
- 2. 图遍历算法(Traversal algorithm)
- 2.1 深度优先搜索(Depth First Search,DFS)
- 2.2 广度优先搜索(Breadth First Search,BFS)
- 2.3 总结
- 3. 加权图(Weighted Graph)
- 3.1 单源最短路径问题(Single-Source Shortest Path problem,SSSP)
- 3.2 Dijkstra算法
- 3.2.1 Dijkstra算法的局限性
- 4. 最小生成树(MST)
- 4.1 Prim 算法
- 4.2 Kruskal 算法
- 5. 流网络(Flow Network)
- 5.1 流的主要规则
- 5.2 最大流(Maximum Flow)
- 5.3 割(Cut)
- 5.3.1 割(cut)的流量(flow)和容量(capacity)
- 5.3.2 增广路径(augmenting path)
- 5.4最大流最小割定理(Max-Flow, Min-Cut Theorem)/ Ford-Fulkerson 定理( Ford-Fulkerson Theorem)
- 5.5 Ford-Fulkerson 算法
- 6. 二分图匹配(Bipartite Matching)
- 6.1 最大二分图匹配问题(Maximum Bipartite Matching)
- 6.2 最大二分图匹配问题的算法
1. 图(Graphs)
我们现在进入算法的第二部分,图,这部分也有很多知识我们已经学过。
图是一种可以用来存储、表达和利用连通性信息的数据结构。通过图,可以清晰地表示和处理各种连通性信息,例如在交通网络中表示城市之间的道路连接,在互联网中表示计算机之间的网络连接,在二叉树中表示节点之间的父子关系等。
一个图由两部分组成:
顶点集(Vertices或Nodes):图中的对象集合,用符号 V V V表示。
边集(Edges):顶点之间的成对连接,表示两个顶点之间的关系,用符号 E E E表示。
所以一个图 G G G可以表示为 G = ( V , E ) G=(V,E) G=(V,E),其中: V V V是顶点集, E E E是边集,由 V V V中的顶点对组成。
1.1 边(Edge)的类型
图中的边(Edge)有两种:有向边(Directed edge)和无向边(Undirected edge)
- 有向边(Directed edge)
有向边是顶点对的有序排列 ( u , v ) (u,v) (u,v),其中第一个顶点 u u u是起点(origin),第二个顶点 v v v是终点(destination)。
如图所示。

- 无向边(Undirected edge)
无向边是顶点对的无序排列 ( u , v ) (u,v) (u,v),边没有方向。
如图所示。

1.2 图的类型
我们根据边的类型将图的类型也进行区分。
- 有向图(Directed graph)
图中的所有边都是有向的。
例如,航班网络(flight network)。
如图所示。
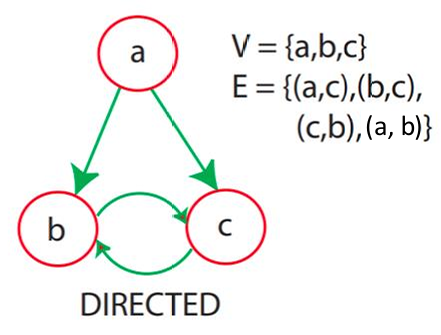
- 无向图(Undirected graph)
图中的所有边都是无向的。
例如,路由网络(route network)。
如图所示。
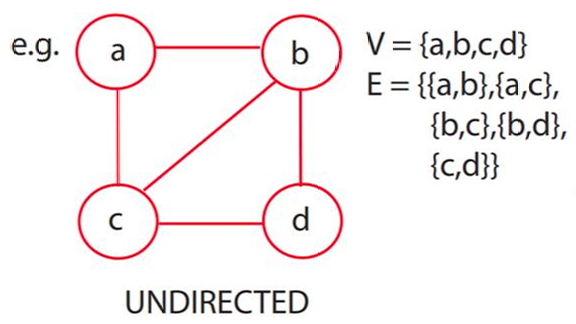
1.3 其他基本术语

- 边的端点(End vertices or endpoints of an edge):
指的是一条边连接的两个顶点。
如图所示, U U U和 V V V是边 a a a的端点。 - 顶点的关联边(Incident edges on a vertex):
指的是所有连接到该顶点的边。
如图所示, a a a, d d d, b b b是顶点 V V V的关联边。 - 相邻顶点(Adjacent vertices):
指的是通过一条边直接相连的两个顶点。
如图所示, U U U和 V V V是相邻顶点,因为边 a a a。 - 顶点的度(Degree of a vertex):
指的是与该顶点关联的边的数量。
如图所示, V V V的度是3。

- 路径(Path):
路径是一系列交替出现的顶点和边,开始和结束于顶点。
每条边都由其端点前后相连。路径可以包含重复的顶点和边。 - 简单路径(Simple path):
简单路径是一种特殊的路径,其中所有的顶点和边都是不同的,即路径中没有重复的顶点和边。
所以图中 P 1 P_1 P1, P 2 P_2 P2都是路径,但是只有 P 1 P_1 P1是简单路径。
1.4 子图(Subgraph)
-
子图(Subgraph)
子图 H H H是图 G G G的一个图,其顶点和边都是 G G G的顶点和边的子集。
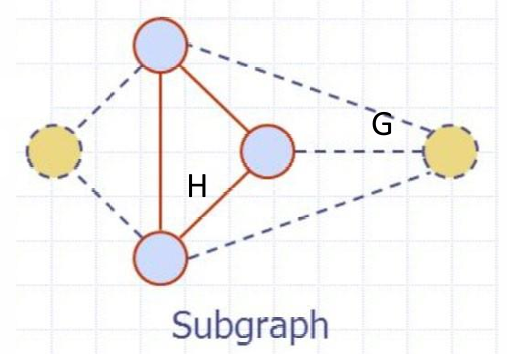
-
生成子图(Spanning Subgraph)
生成子图是包含 G G G所有顶点的 G G G的子图。
生成子图是原图的一个子图,但它包含了原图中所有的顶点。生成子图可以包含原图中的一部分边,也可以包含所有的边。
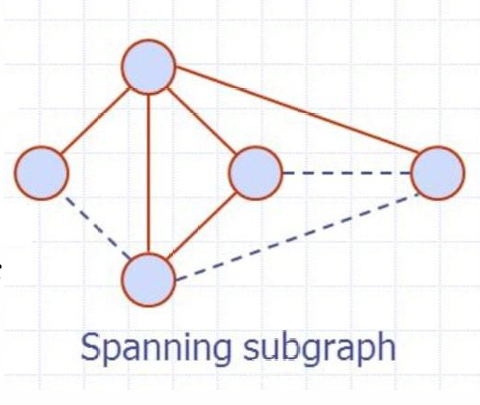
-
连通图(Connected graph)
如果对于图中任意两个不同的顶点,都存在一条路径连接它们,则称该图为连通图。 -
连通分量(Connected components)
如果图 G 不是连通的,那么它的最大的连通子图被称为 G 的连通分量。 -
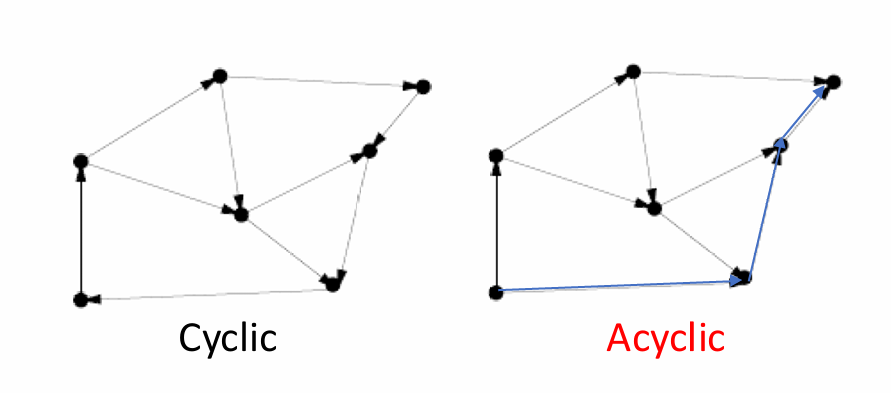
无环图(Acyclic graph)
无环图是一种不包含任何环(cycle)的图。例如树就是一种特殊的无环图,它是连通的且无环的无向图。 -
有向无环图(Directed Acyclic Graphs, DAGs)
有向无环图是一种所有边都有方向的无环图。
下图展示了一个有环图和无环图。
1.5 树(Tree)
- 树(Tree):
向前面所说,树是一种特殊的无向图,满足以下条件:
连通性:图中任意两个顶点之间都有路径相连。
无环性:图中不存在环。
这种定义的树与有根树(Rooted tree)不同。有根树是指具有一个特定起始顶点(根)的树,而这里定义的树没有指定根。

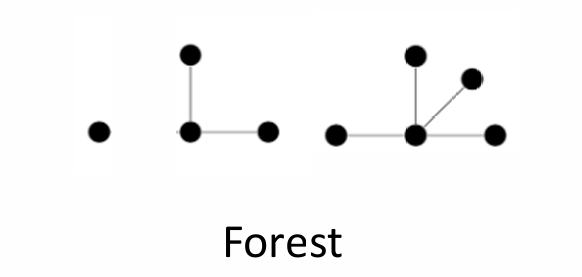
- 森林(Forest):
森林顾名思义是很多树,所以森林是一种无向图,它不包含任何环,森林中的连通分量(Connected components)都是树。所以森林可以由多个不相连的树组成。
1.5.1 树的性质
因此我们现在可以根据这里的定义获取一些性质。如果图 G G G是一个无向图,其有 n n n个顶点和 m m m条边。
- 如果 G G G是连通的,那么 m ≥ n − 1 m≥n−1 m≥n−1。
- 如果 G G G是树,那么 m = n − 1 m=n−1 m=n−1。
- 如果 G G G是森林,那么 m ≤ n − 1 m≤n−1 m≤n−1。
在任何有两个或更多节点的树中,至少有两个节点的度数为 1 1 1,这些节点称为叶子节点(leaf nodes)。
因为树是一种无环连通图,如果一个顶点的度数大于 1 1 1,那么它至少有两个邻居,而树的边数是 n − 1 n−1 n−1,所以至少有两个顶点的度数为 1 1 1。
我们现在选中任何一颗树,我们每次移除一个叶节点,就会移除一个顶点和一条边,最后会剩下一个顶点,因此我们证明了第二条性质的正确性。

因此对于第三条性质我们也很容易证明,因为森林是树组成的,对于树来说 m = n − 1 m=n−1 m=n−1了,我们每多一棵树这里 − 1 -1 −1的数量就会越多。
也就是 m 1 = n 1 − 1 m_1=n_1−1 m1=n1−1, m 2 = n 2 − 1 m_2=n_2−1 m2=n2−1,…, m k = n k − 1 m_k=n_k−1 mk=nk−1。
m 1 + m 2 + . . . + m k = n 1 + n 2 + . . . + n k − k m_1+m_2+...+m_k=n_1+n_2+...+n_k-k m1+m2+...+mk=n1+n2+...+nk−k
因此 m = n − k m=n-k m=n−k,其中 k ≥ 1 k≥1 k≥1,所以 m ≤ n − 1 m≤n−1 m≤n−1。
1.5.2 生成树(Spanning Tree)和生成森林(Spanning Forest)
生成树是连通图的一个生成子图,它本身是一棵树。
生成树不是唯一的,除非原图本身就是一棵树。
生成树在设计通信网络中有应用,可以用来找到连接所有节点的最小成本路径。
生成森林是图的一个生成子图,它本身是一个森林。
2. 图遍历算法(Traversal algorithm)
图遍历是指按照某种策略访问图中的所有顶点和边的过程。
2.1 深度优先搜索(Depth First Search,DFS)
故名意思以深度为优先。
从起点出发,沿着一条路径一直向前探索,直到无法继续前进为止。当到达一个无法继续前进的顶点时,算法会回溯(即回到上一个顶点)并尝试其他未探索的路径。这个过程会重复进行,直到图中的所有顶点都被访问过。
伪代码如下。

这是使用递归的算法,如果我们想不使用递归的话,我们可以使用栈(Stack)去模拟递归调用。
伪代码如下。

将起始顶点推入栈中,并标记为已访问。
当栈不为空时,执行以下操作:
从栈顶取出一个顶点(这是我们接下来要探索的顶点)。
检查是否存在从 u u u到 w w w的边,且 w w w未被访问过。
如果存在这样的边,将 w w w推入栈,标记 w w w为已访问,设置 u u u为 w w w的父节点,将边 ( u , w ) (u,w) (u,w)标记为发现边。
如果不存在未访问的相邻顶点,但存在从 u u u到 w w w的边,且 w w w已被访问过且边 ( u , w ) (u,w) (u,w)未被标记,将边 ( u , w ) (u,w) (u,w)标记为回边(back edge)。
如果没有符合条件的边,从栈中弹出 u u u
重复上述过程,直到栈为空。
如图所示,我们从 A A A出发,因此我们第一步将 ( A , E ) (A,E) (A,E)添加到深度优先搜索树中,因此 E E E被推入栈。
第二步看现在栈顶 E E E,将 ( E , F ) (E,F) (E,F)添加到深度优先搜索树中,因此 F F F被推入栈。
第三步看现在栈顶 F F F,将 ( F , C ) (F,C) (F,C)添加到深度优先搜索树中,因此 C C C被推入栈。
第四步看现在栈顶 C C C,将 ( C , D ) (C,D) (C,D)添加到深度优先搜索树中,因此 D D D被推入栈。
第五步看现在栈顶 D D D,由于 D D D不存在未访问的相邻顶点,所以我们标记 ( D , F ) (D,F) (D,F)标记为回边(back edge)。然后没有相邻顶点了,所以弹出 D D D。
第六步看现在栈顶 C C C,将 ( C , B ) (C,B) (C,B)添加到深度优先搜索树中,因此 B B B被推入栈。
第七步看现在栈顶 B B B,剩余的边都是回边,我们再弹出 B B B。
后续我们检查每次堆顶元素,不断弹出,将 ( F , A ) (F,A) (F,A)也标记为回边,最后弹出栈顶 A A A,栈便空了。
结果如下。
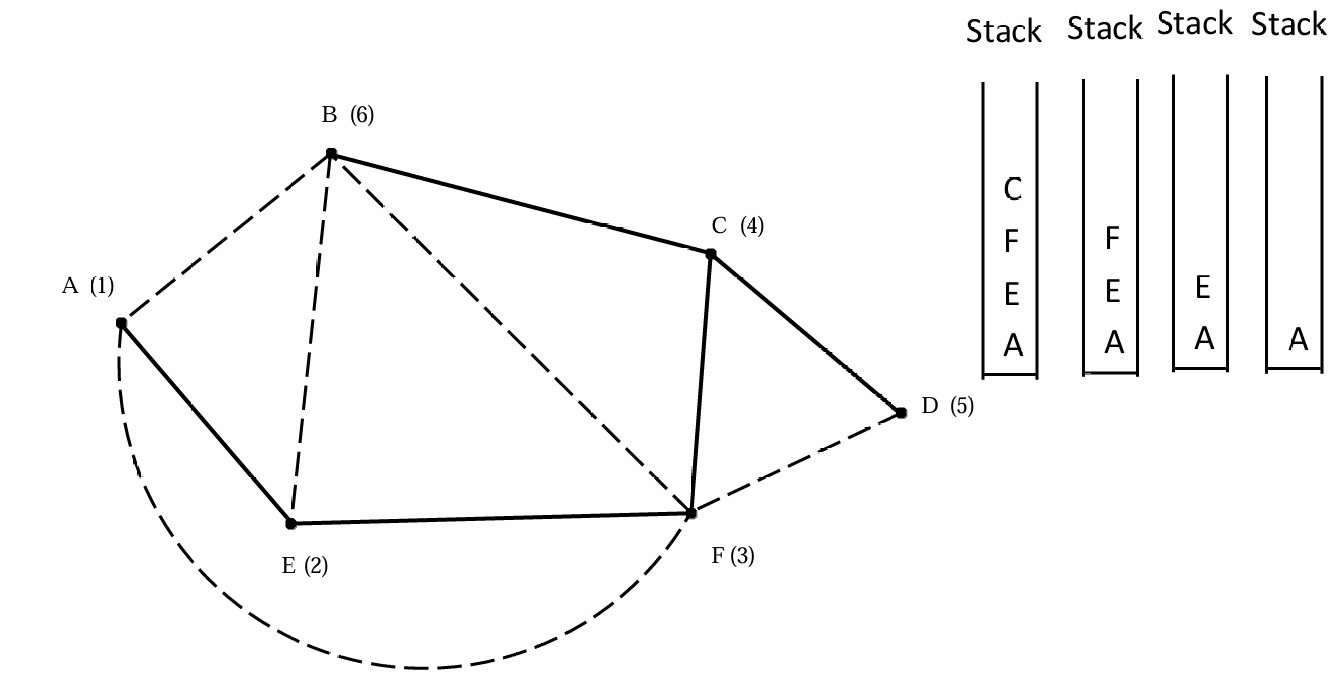
实线是搜索树内容,虚线是回边。
2.2 广度优先搜索(Breadth First Search,BFS)
广度优先搜索(Breadth First Search,BFS)从图中的某个顶点开始,首先探索该顶点的所有相邻顶点(即第一层邻居),然后依次探索下一层的顶点,直到所有顶点都被访问过。
因此DFS生成的搜索树通常是“长而细”的,因为它倾向于深入探索一条路径,直到尽头。BFS生成的搜索树通常是“短而宽”的,因为它同时探索同一层次的所有顶点。
我们这里使用队列(Queue)数据结构来控制顶点的访问顺序。
伪代码如下。

将起始顶点 v v v入队到队列 Q Q Q中,标记顶点 v v v为已访问。当队列 Q Q Q不为空时,从队列中取出一个顶点 u u u,遍历所有与 u u u未标记的相邻的边 ( u , w ) (u,w) (u,w),如果顶点 w w w未被访问过,则将边 ( u , w ) (u,w) (u,w)标记为发现边(discovery edge),标记顶点 w w w为已访问,将顶点 w w w入队到队列 Q Q Q中。否则将边 ( u , w ) (u,w) (u,w)标记为交叉边(cross edge)。
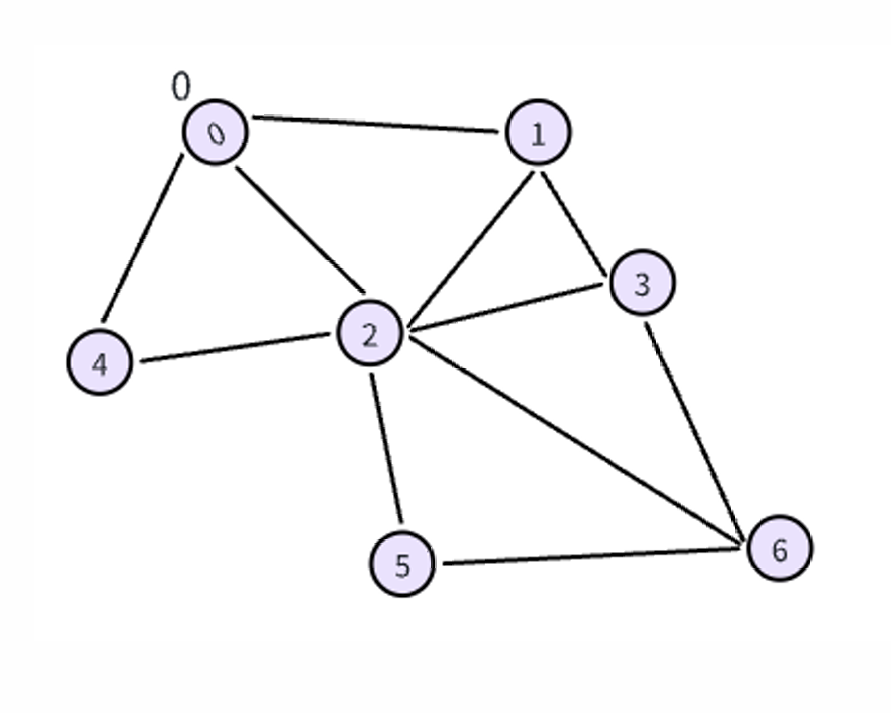
如图所示,第一步我们将 0 0 0入队到队列中,标记0为已访问。从队列中取出 0 0 0, 0 0 0有三条相邻的边,这些边的顶点都未被访问过,所以将这些边都标记为发现边,并标记这些边的顶点为已访问,将它们放入队列中。
第二步,我们从队列中拿出 1 1 1, 1 1 1有 2 2 2条边还未标记,其中 ( 1 , 2 ) (1,2) (1,2)是交叉边,而 ( 1 , 3 ) (1,3) (1,3)被标记为发现边,将 3 3 3标记为已访问,并放入队列中。
第三步,从队列中拿出 2 2 2, 2 2 2有 4 4 4条边还未标记,其中 ( 2 , 3 ) (2,3) (2,3), ( 2 , 4 ) (2,4) (2,4)是交叉边,而 ( 2 , 5 ) (2,5) (2,5), ( 2 , 6 ) (2,6) (2,6)被标记为发现边,将 5 , 6 5,6 5,6标记为已访问,并放入队列中。
后续步骤中不断遍历队列中的顶点,直到队列清空,结果如下。
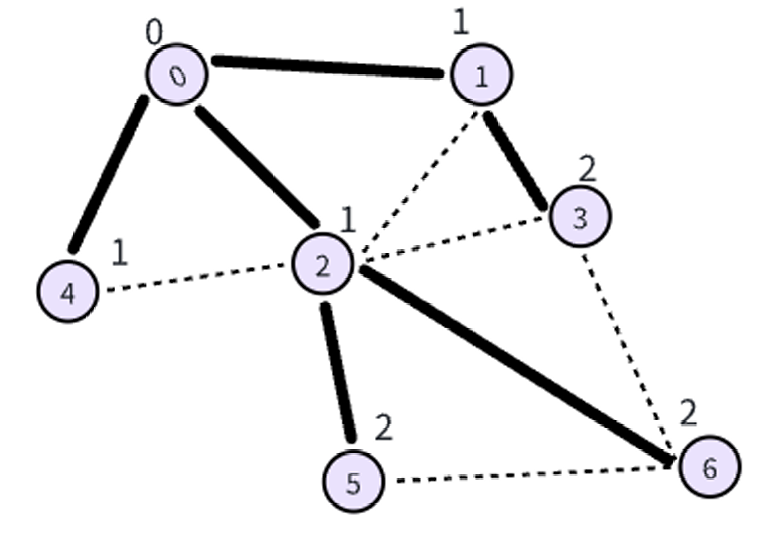
实线是搜索树内容,虚线是交叉边,数字代表它们的深度。
2.3 总结
DFS(深度优先搜索):
DFS 遍历会产生一棵生成树,这棵树包含了图中所有的顶点,并且是无环的。
因此DFS 可以用来检测图中是否存在环。如果在遍历过程中遇到一个已经访问过的顶点,并且这个顶点不是当前顶点的祖先,那么就表明图中存在环。
BFS(广度优先搜索):
BFS 特别适用于在无权图中寻找两个顶点之间的最短路径。在无权图中,所有边的权重相同,因此最短路径就是边数最少的路径。
BFS 从起始顶点开始,逐层探索图中的顶点。这意味着 BFS 会先访问所有与起始顶点相邻的顶点(第一层),然后再访问这些顶点的邻居(第二层),以此类推。这种逐层探索的方式确保了 BFS 找到的是从起始顶点到每个顶点的最短路径。
3. 加权图(Weighted Graph)
我们前面提到了无权图,在无权图中,所有边的权重相同。
加权图是一种图,其中每条边 e e e都有一个与之关联的数值标签 w ( e ) w(e) w(e),这个数值称为边 e e e的权重(weight)。
在加权图中,路径 P P P的长度(或权重)是路径中所有边的权重之和。
如果路径 P P P由边 e 1 , e 2 , … , e k e_1 ,e_2 ,…,e_k e1,e2,…,ek组成,那么路径 P P P的权重 w ( P ) w(P) w(P)可以表示为: w ( P ) = ∑ i = 1 k w ( e i ) w(P) = \sum_{i=1}^{k} w(e_i) w(P)=∑i=1kw(ei)
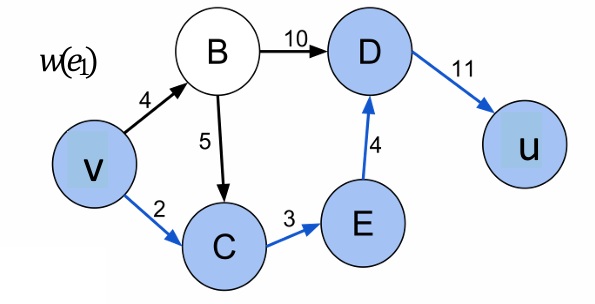
如图所示,路径V-B-D-U的权重是25,路径V-B-C-E-D-U的权重是27,路径V-C-E-D-U的权重是20。
以最后一个为例, w ( P ) = 2 + 3 + 4 + 11 = 20 w(P) = 2+3+4+11 = 20 w(P)=2+3+4+11=20。
3.1 单源最短路径问题(Single-Source Shortest Path problem,SSSP)
顶点 v v v到顶点 u u u的距离:在图 G G G中,从顶点 v v v到顶点 u u u的距离,记作 d ( v , u ) d(v,u) d(v,u),是指从顶点 v v v到顶点 u u u的所有路径中长度(或权重)最小的那条路径的值。
因此我们现在可以考虑在加权图中,给定一个固定的顶点 v v v,找到从顶点 v v v到图中所有其他顶点 u ( u ≠ v ) u(u≠v) u(u=v)的最短路径。这里,边的权重被视为距离。
3.2 Dijkstra算法
其实我们可以使用贪心算法去解决SSSP问题,Dijkstra算法就是使用贪心算法解决这类的算法,我们在之前的算法和计网中都学习过这个算法。它假设图中所有边的权重都是非负的。
伪代码如下。

将源顶点 v v v到自身的距离设为 0 0 0,且将源顶点 v v v到所有其他顶点的距离设为无穷大,再将所有顶点的前驱初始化为 n u l l null null。
使用一个优先队列(堆) Q Q Q来存储所有顶点,初始时所有顶点都在队列中,使用距离标签 D D D作为键。创建一个空集合 C C C来存储已经被确定最短路径的顶点。
当优先队列 Q Q Q不为空时,执行以下操作:
从未访问顶点中提取距离源点最近的顶点 u u u,将顶点 u u u添加到集合 C C C中,标记为已处理,遍历顶点 u u u的所有邻接顶点 z z z:
如果通过顶点 u u u到顶点 z z z的距离比当前已知的最短距离更短,即如果 D [ u ] + w ( u , z ) < D [ z ] D[u]+w(u,z)<D[z] D[u]+w(u,z)<D[z](其中 D [ u ] D[u] D[u]是从源点 v v v到顶点 u u u的当前最短路径长度, w ( u , z ) w(u,z) w(u,z)是边 u u u到 z z z的权重或距离。)则更新顶点 z z z的最短距离,即更新 D [ z ] D[z] D[z]为 D [ u ] + w ( u , z ) D[u]+w(u,z) D[u]+w(u,z),并更新顶点 z z z在优先队列中的键以及顶点 z z z的前驱为顶点 u u u。
最后返回最终的距离数组 D D D,前驱数组 P P P,以及最终状态集合 C C C。其中距离列表 D D D存储每个顶点的最短路径长度,前驱节点数组 P P P用于追踪和重建路径,集合 C C C记录已经找到最短路径的顶点,避免重复处理。
下面给出一个例子,其中d点是起点。
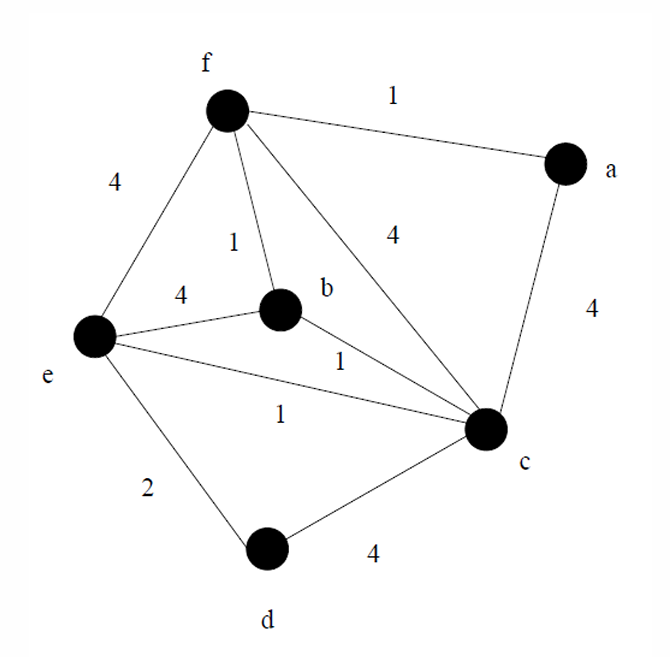
距离数组 D D D,前驱数组 P P P,以及最终状态集合 C C C的变化过程如下。
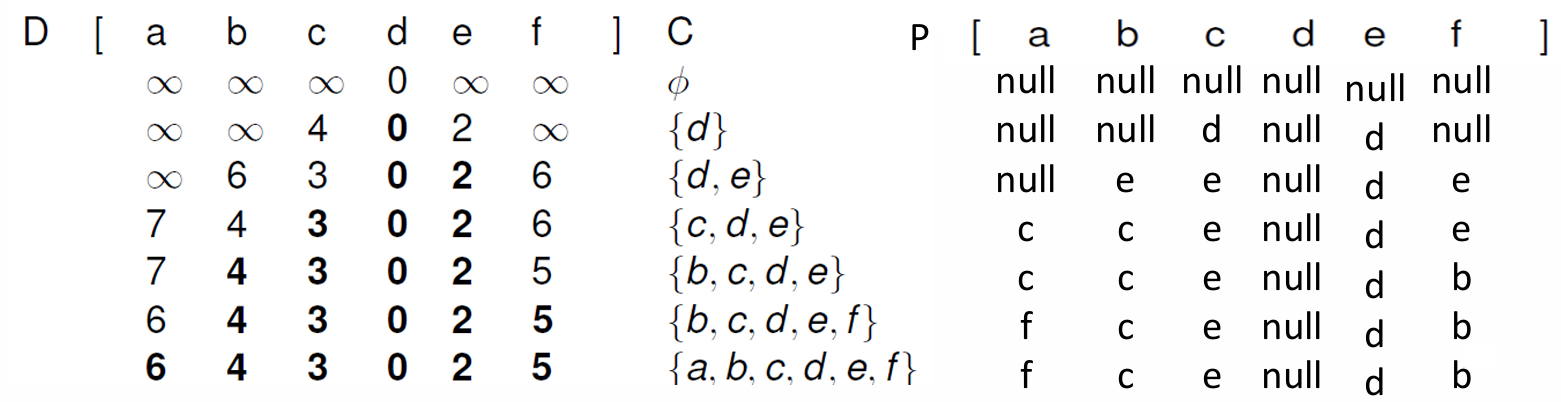
第一步选择 d d d顶点,第二步选择周围最短的,即 e e e顶点,第三步选择 c c c顶点,第四步选择 b b b顶点,第五步选择 f f f顶点,第六步选择 a a a顶点。
3.2.1 Dijkstra算法的局限性
前面我们就提到Dijkstra算法不适用于包含负权重边的图,贪心策略在负权重边的情况下可能导致错误结果。
如下图所示。
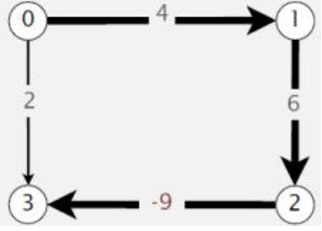
最短路径是(0,1,2,3)而不是(0,3)。
一种尝试解决这个问题的方法是对所有边的权重进行重新加权,例如,给每条边的权重加上一个常数,以消除负权重。如下图所示。
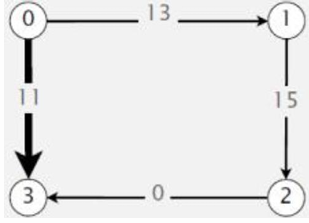
这里最短路径是(0,3)了。
包含负权重边的图,需要使用不同的算法,如Bellman-Ford算法。Bellman-Ford算法能够处理负权重边,并且能够检测图中是否存在负权重环。
4. 最小生成树(MST)
G G G是一个无向图,图中的每条边都有一个权重或成本。
最小生成树是满足以下条件的 G G G的子图:
- 包含 G G G的所有顶点。
- 不包含任何环,即它形成一个树形结构。
- 在所有可能的生成树中,边权重之和最小的生成树。
最小生成树的应用如下。
- 网络设计:
在计算机网络和电信网络的设计中,MST 可以用来找到连接所有节点的最小成本网络。
例如,在设计一个城市的交通网络或电力网络时,可以使用 MST 来确定连接所有区域的最小成本方案。 - 近似算法和聚类分析的基础:
MST 算法可以作为许多近似算法的基础,这些算法用于解决更复杂的问题,如旅行商问题(TSP)等。
在聚类分析中,MST 可以用来识别数据点之间的相似性,从而帮助将数据分组。
4.1 Prim 算法
为了生成最小生成树,我们使用贪心策略的Prim 算法。
算法细节如下。
先将起始顶点加入到生成树中,初始化一个空的顶点集合 T,其中 T 表示当前生成树中的顶点。
重复以下步骤直到所有顶点都被加入到生成树中:
从集合 T T T中的顶点到 T T T外的顶点的所有边中,选择权重最小的边,这条边被称为“最小附着成本”边。
将这条边及其连接的 T T T外的顶点加入到生成树中。
在添加边的过程中,需要确保不会形成环。由于每次只添加连接 T T T内顶点和 T T T外顶点的边,因此自然避免了环的形成。
伪代码如下。

这里集合 T T T,用于存储生成树的边。集合 U U U储存已访问的顶点。
所以Prim 算法通过以下关键步骤构建最小生成树:
- 包含所有顶点:从单个顶点开始,逐步扩展到包含所有顶点。
- 避免环:只选择连接树内和树外顶点的边,防止环的形成。
- 最小化总边权重:在每一步选择最小权重的边,确保生成树的总权重最小。
下面给出一些例子。
例1:
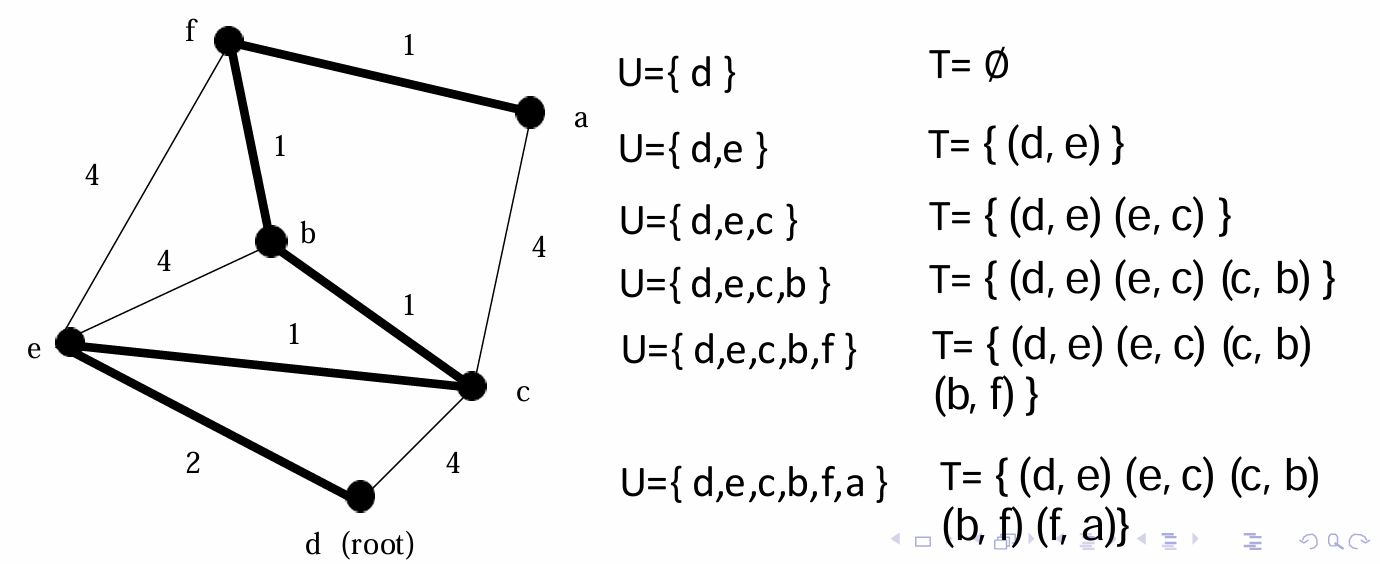
上图左侧是无向图,右侧是集合 U U U和 T T T的演变过程。
例2:
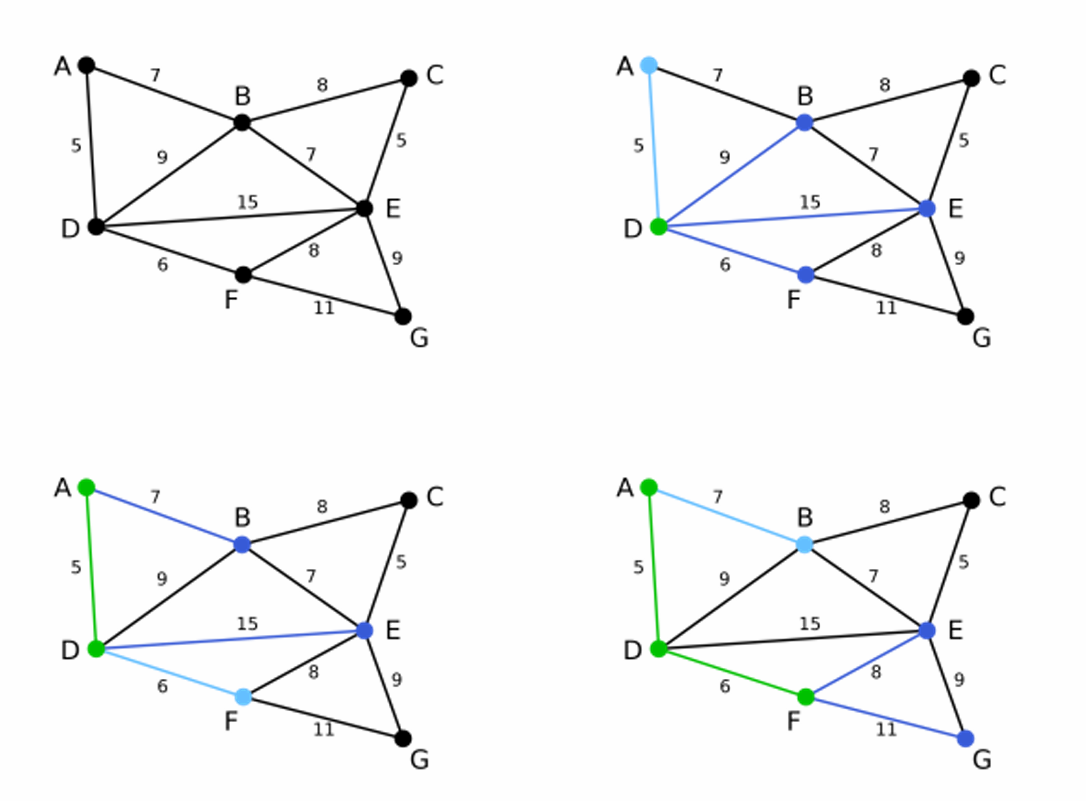
绿色代表集合的结果,每一步的演变如图所示。
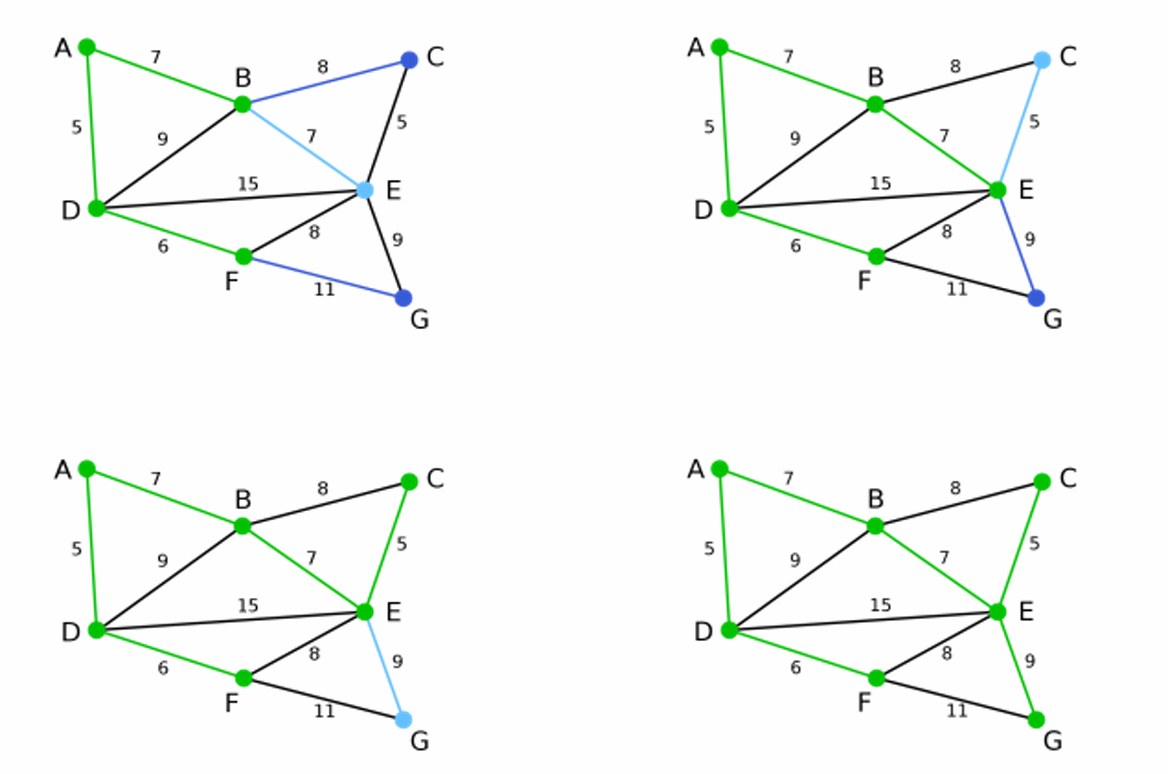
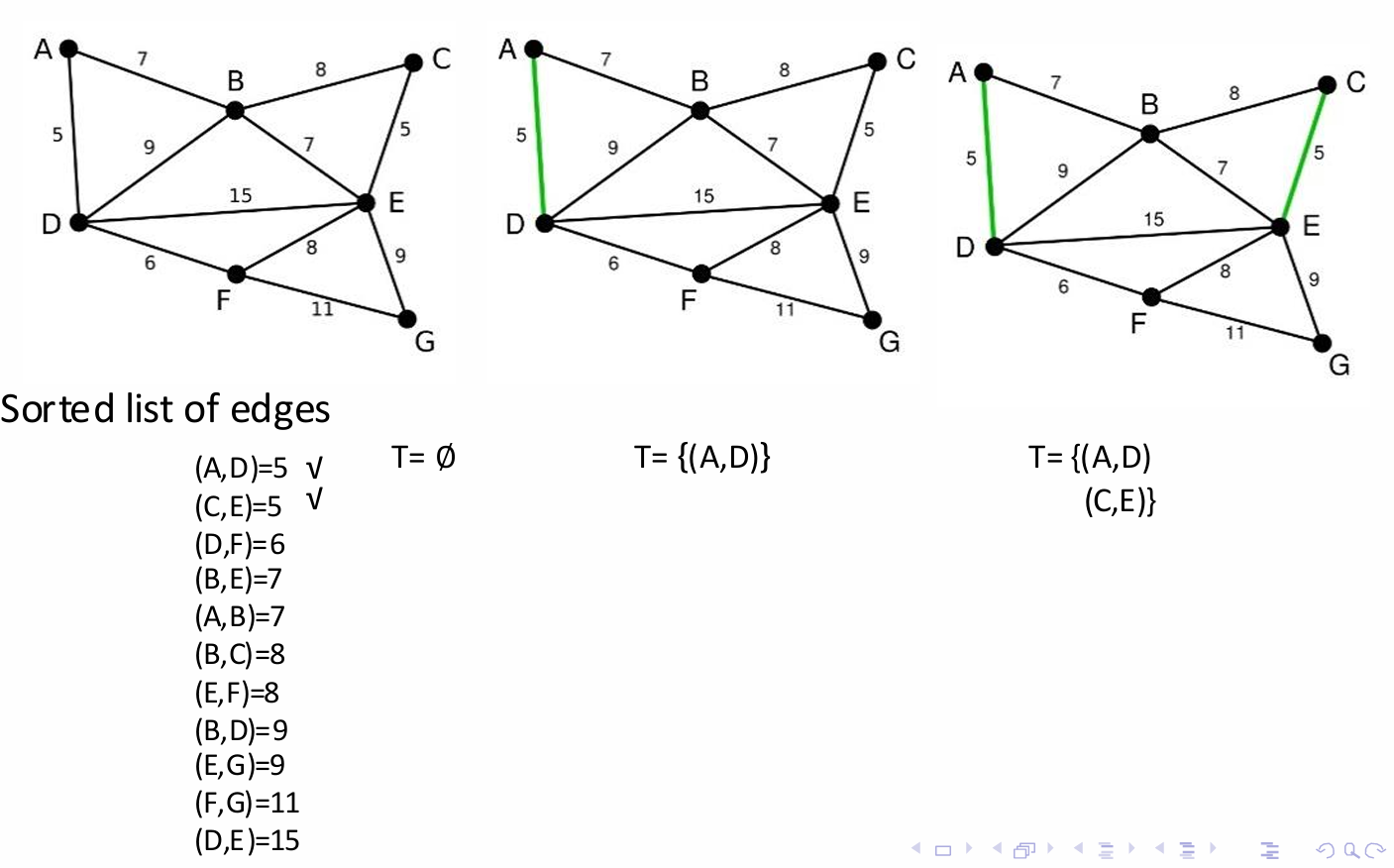
4.2 Kruskal 算法
Kruskal算法也是贪心策略,但是与Prim算法不同,Kruskal算法不是从一个顶点开始逐步扩展生成树,而是按照边的权重从小到大的顺序考虑所有边。
算法的细节如下。
首先将图中的所有边按照权重从小到大排序。
然后从权重最小的边开始,贪心地选择边,但前提是添加这条边不会与已选择的边形成环。
重复这个过程,直到生成树包含图中的所有顶点。
如图所示。
我们将图里所以的边按照权重从小到大排序。
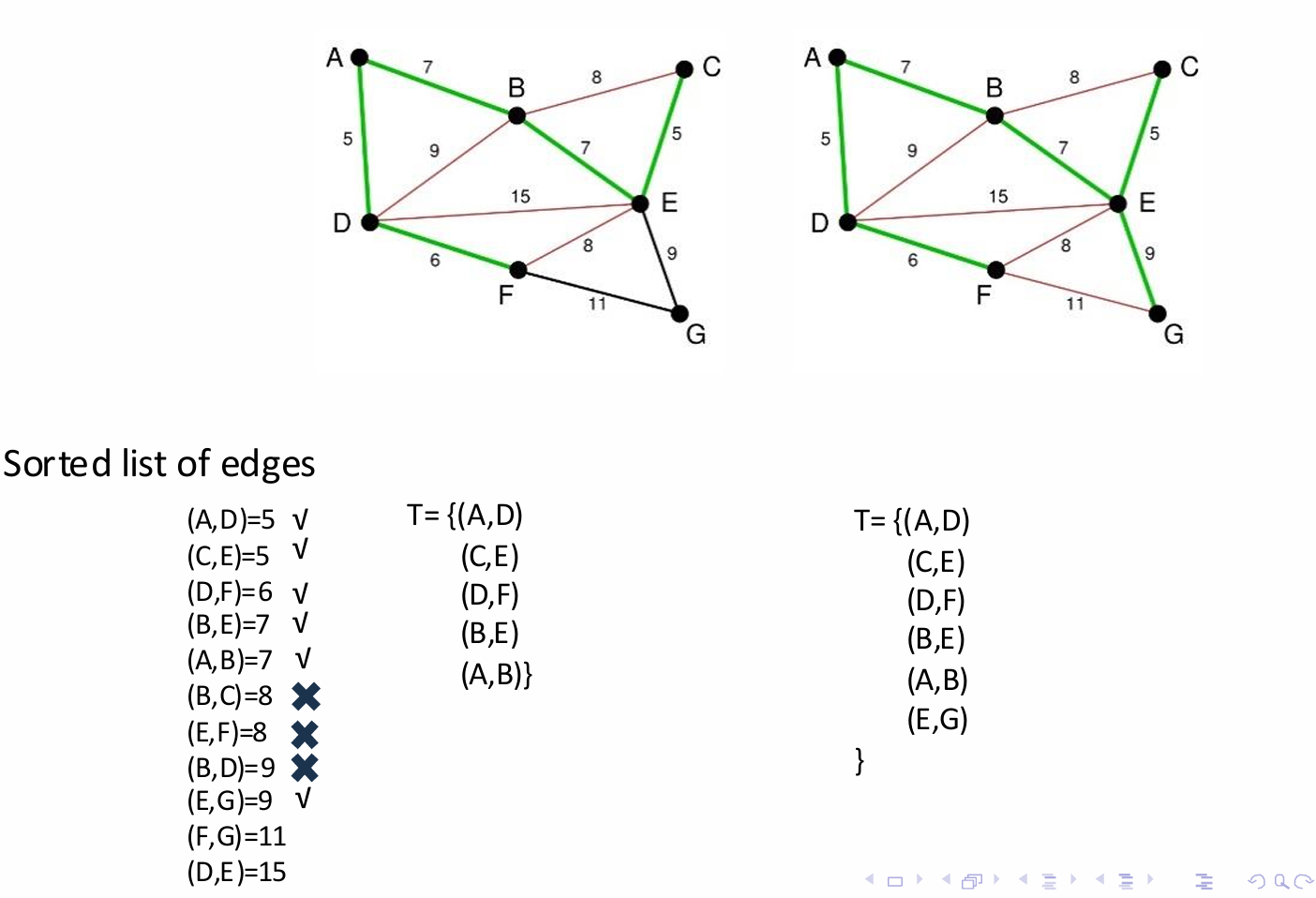
不断添加直到包含所有顶点。
5. 流网络(Flow Network)
一个流网络 N N N由以下部分组成:
- 加权有向图 G G G: G G G是一个有向图(digraph),图中的每条边都有一个非负整数权重。而边的权重称为边的容量(capacity),记作 c ( e ) c(e) c(e)。
- 两个特殊的顶点:
源点(source):记作 s s s,是图中的一个顶点,它没有入边(即没有边指向 s s s)。
汇点(sink):记作 t t t,是图中的另一个顶点,它没有出边(即没有边从 t t t出发)。
下面给出一个例子。
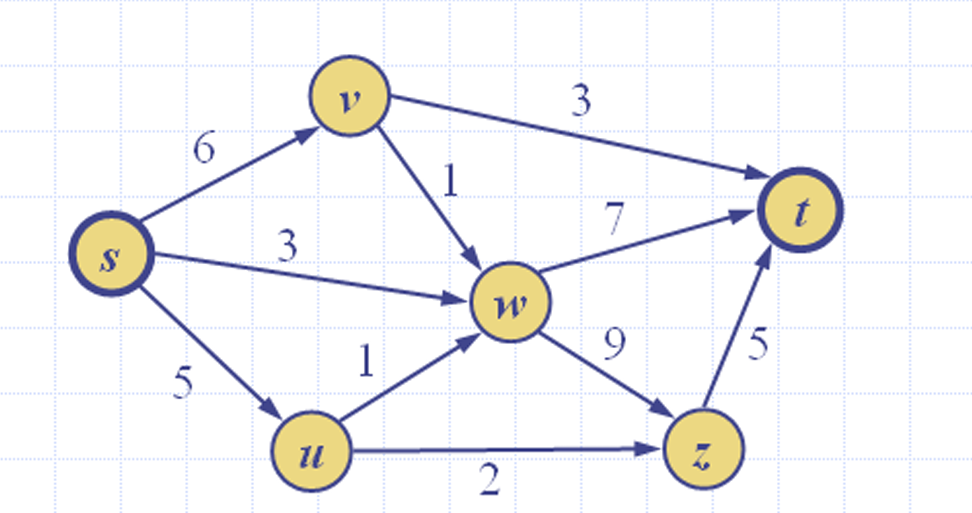
5.1 流的主要规则
流网络中有两个主要规则:容量规则和守恒规则。
- 容量规则(Capacity Rule):
对于图中的每条边 e e e,流 f ( e ) f(e) f(e)必须满足 0 ≤ f ( e ) ≤ c ( e ) 0≤f(e)≤c(e) 0≤f(e)≤c(e),其中 c ( e ) c(e) c(e)是边 e e e的容量。这意味着流不能超过边的容量。 - 守恒规则(Conservation Rule):
对于图中的每个顶点 v v v(除了源点 s s s和汇点 t t t),流入 v v v的总流量必须等于流出 v v v的总流量。
数学表达式为: ∑ e ∈ E − ( v ) f ( e ) = ∑ e ∈ E + ( v ) f ( e ) ∑_{e∈E^− (v)}f(e)=∑_{e∈E^+ (v)}f(e) ∑e∈E−(v)f(e)=∑e∈E+(v)f(e)其中, E − ( v ) E^− (v) E−(v)是指向顶点 v 的边的集合(即流入边), E + ( v ) E^+ (v) E+(v)是从顶点 v v v出发的边的集合(即流出边)。
5.2 最大流(Maximum Flow)
我们再介绍一个概念。
流的值:流 f f f的值,记作 ∣ f ∣ ∣f∣ ∣f∣,是从源点 s s s到汇点 t t t的总流量。这等于流入汇点 t t t的总流量。
所以我们有了一个新概念——最大流。
最大流:对于一个网络 N N N,如果一个流的值是该网络所有可能流中最大的,那么这个流就被称为最大流。
我们后面就要研究找到具有最大值的流,即解决最大流问题。
前面的例子的结果如下。

这里是最大流的值 10 10 10,即 4 + 3 + 3 4+3+3 4+3+3或 3 + 3 + 4 3+3+4 3+3+4。
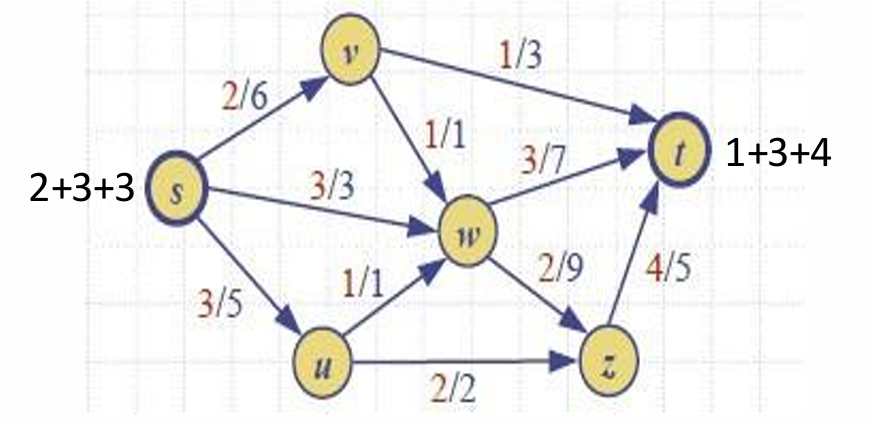
而这张图的流的值为 8 8 8,并非最大流。
下面我们将研究这个结果是怎么计算的。
5.3 割(Cut)
为了解决最大流问题,我们介绍割(Cut)这个概念。
割:在具有源点 s s s和汇点 t t t的网络 N N N中,割 X X X是将顶点集 V V V分成两个子集 V s V_s Vs和 V t V_t Vt的划分,使得源点 s s s属于 V s V_s Vs,汇点 t t t属于 V t V_t Vt。
前向边(Forward edge):在割 X X X中,前向边是从 V s V_s Vs到 V t V_t Vt的边,即起点在 V s V_s Vs,终点在 V t V _t Vt。
后向边(Backward edge):在割 X X X中,后向边是从 V t V_t Vt到 V s V_s Vs的边,即起点在 V t V_t Vt,终点在 V s V_s Vs。
如图所示。
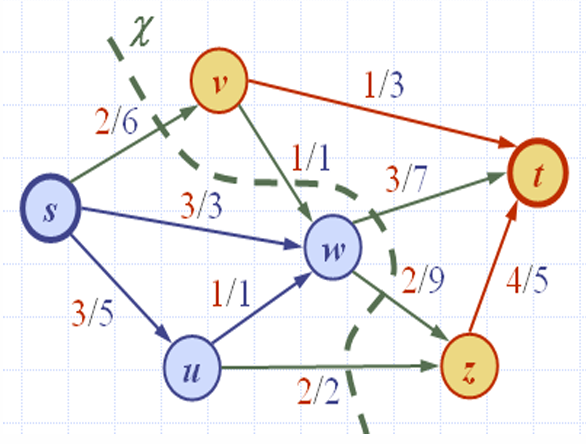
绿色的线是割(Cut)。
V s = { s , u , w } V_s=\{s,u,w\} Vs={s,u,w}
V t = { v , t , z } V_t=\{v,t,z\} Vt={v,t,z}
前向边(Forward edge): { ( s , v ) , ( w , t ) , ( w , z ) , ( u , z ) } \{(s,v),(w,t),(w,z),(u,z)\} {(s,v),(w,t),(w,z),(u,z)}
后向边(Backward edge): { ( v , w ) } \{(v,w)\} {(v,w)}
5.3.1 割(cut)的流量(flow)和容量(capacity)
割的流量 f ( χ ) f(χ) f(χ)指的是所有前向边的流量之和减去所有后向边的流量之和。
如前面例子中, f ( χ ) = ( 2 + 3 + 2 + 2 ) − ( 1 ) = 8 f(χ)=(2+3+2+2)-(1)=8 f(χ)=(2+3+2+2)−(1)=8
割的容量 c ( χ ) c(χ) c(χ)指的是所有前向边的容量之和。
如前面例子中, c ( χ ) = 6 + 7 + 9 + 2 = 24 c(χ)=6+7+9+2=24 c(χ)=6+7+9+2=24
不同的割可能会有不同的容量,但是对于确定的流网络(流值已经确定的网络),任何割的流量值 f ( χ ) f(χ) f(χ)是相同的。
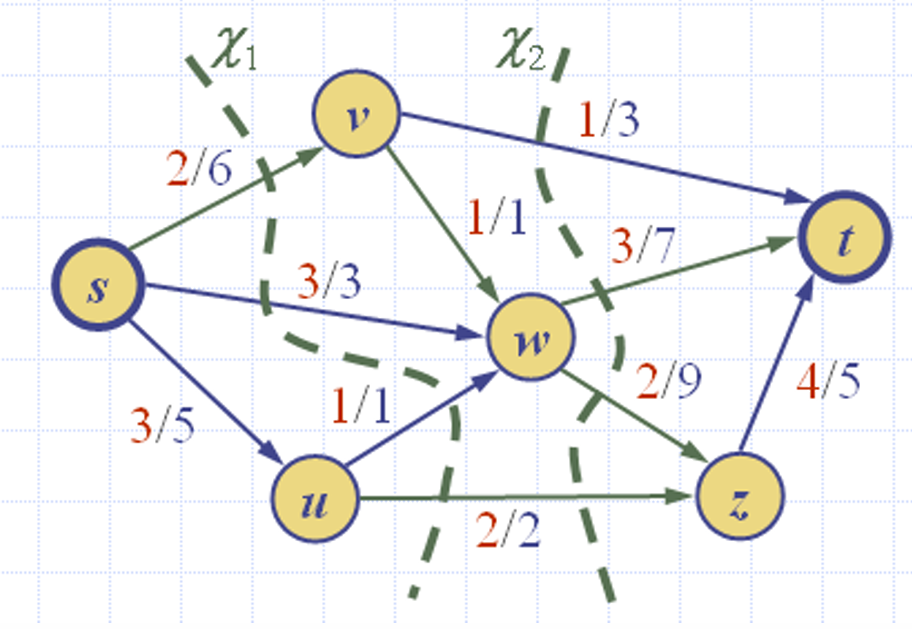
如图所示,这里的 c ( χ 1 ) = 6 + 3 + 1 + 2 = 12 c(χ_1)=6+3+1+2=12 c(χ1)=6+3+1+2=12,
c ( χ 2 ) = 3 + 7 + 9 + 2 = 21 c(χ_2)=3+7+9+2=21 c(χ2)=3+7+9+2=21,
而两个割的流量都是 ∣ f ∣ = 8 |f| = 8 ∣f∣=8。
因此我们介绍两个引理。
引理1(Lemma 1):
对于任何流网络 N N N和该网络的流 f f f,流的值(即从源点 s s s到汇点 t t t的总流量)等于穿过任何割 χ χ χ的流量。数学表达式为 ∣ f ∣ = f ( χ ) ∣f∣=f(χ) ∣f∣=f(χ)。
这个引理1就对应的前面刚刚说的那个例子。这其实因为我们前面说的守恒规则。
引理 2 (Lemma 2):
对于任何流网络 N N N和该网络的割 χ χ χ,给定任何流 f f f,穿过割的流量不会超过该割的容量。数学表达式为 f ( χ ) ≤ c ( χ ) f(χ)≤c(χ) f(χ)≤c(χ)。
这个也好理解,因为前面的容量规则告诉我们对于图中的每条边 e e e,流 f ( e ) f(e) f(e)必须满足 0 ≤ f ( e ) ≤ c ( e ) 0≤f(e)≤c(e) 0≤f(e)≤c(e)。
我们再介绍一个定理。
定理 1 (Theorem 1):
任何流的值都不大于或等于任何割的容量。数学表达式为 ∣ f ∣ ≤ c ( χ ) ∣f∣≤c(χ) ∣f∣≤c(χ)。
也就是说最大流的值不会超过最小割的容量。这意味着如果我们能找到一个割,其容量是所有割中最小的,那么这个割的容量就是网络中可能的最大流量。
5.3.2 增广路径(augmenting path)
为了解决最大流问题,我们还需要知道一个概念——增广路径(augmenting path)。
首先对于网络 N N N中的流 f f f,考虑从顶点 u 到顶点 v v v的边 e e e:
从 u u u到 v v v的残余容量(Residual capacity): ∆ f ( u , v ) = c ( e ) − f ( e ) ∆f (u,v ) = c(e) − f (e) ∆f(u,v)=c(e)−f(e),表示边 e e e还能增加的最大流量。
从 v v v到 u u u的残余容量(Residual capacity): ∆ f ( v , u ) = f ( e ) ∆f (v,u) = f (e) ∆f(v,u)=f(e),表示边 e e e可以减少的流量或反向增加的流量。
那么我们可以将这个残余容量扩大到路径,对于路径的残余容量(Residual capacity of a path),我们考虑从源点 s s s到汇点 t t t的路径 π π π,路径 π π π的残余容量 ∆ f ( π ) ∆_f(π) ∆f(π)是路径上从 s s s到 t t t方向的边的残余容量中的最小值,即 ∆ f ( π ) = m i n ∆ f ( u , v ) , ( u , v ) ∈ π ∆_f(π)=min∆_f(u,v),(u,v)∈π ∆f(π)=min∆f(u,v),(u,v)∈π,这就相当于是木桶效应,因为超过这个最小值,就无法再增加了。
所以我们现在获得了增广路径的定义,如果路径 π π π从 s s s到 t t t的残余容量 ∆ f ( π ) > 0 ∆_f(π)>0 ∆f(π)>0,则路径 π π π是一条增广路径。
下面给出一个例子。
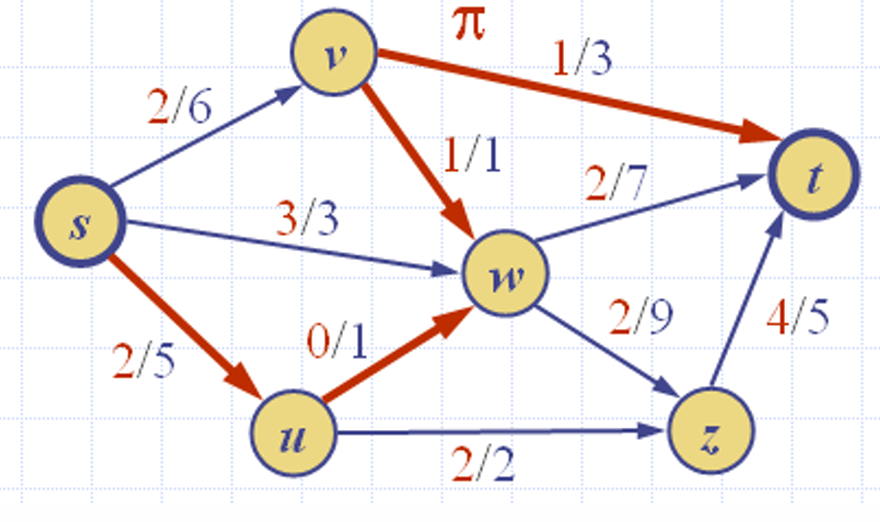
其中 ∆ f ( s , u ) = 3 , ∆ f ( u , w ) = 1 , ∆ f ( w , v ) = 1 , ∆ f ( v , t ) = 2 ∆f(s,u) =3, ∆f(u,w) =1, ∆f(w,v) = 1, ∆f(v,t) =2 ∆f(s,u)=3,∆f(u,w)=1,∆f(w,v)=1,∆f(v,t)=2, ∆ f ( π ) = 1 ∆f (π) = 1 ∆f(π)=1因为 ∆ f ( z , t ) = 1 ∆f (z,t) = 1 ∆f(z,t)=1,而 ∣ f ∣ = 7 |f | = 7 ∣f∣=7。
而我们红线标出来的就是一条增广路径,因为这条路径的残余容量 ∆ f ( π ) = 1 > 0 ∆_f(π)=1>0 ∆f(π)=1>0。
我们现在可以利用流增广(Flow Augmentation)来构建最大流。
首先找到一条从源点 s s s到汇点 t t t的增广路径(augmenting path),然后沿着这条路径增加流量,从而得到一个新的有效流。
所以这也是我们的引理 3(Lemma 3):
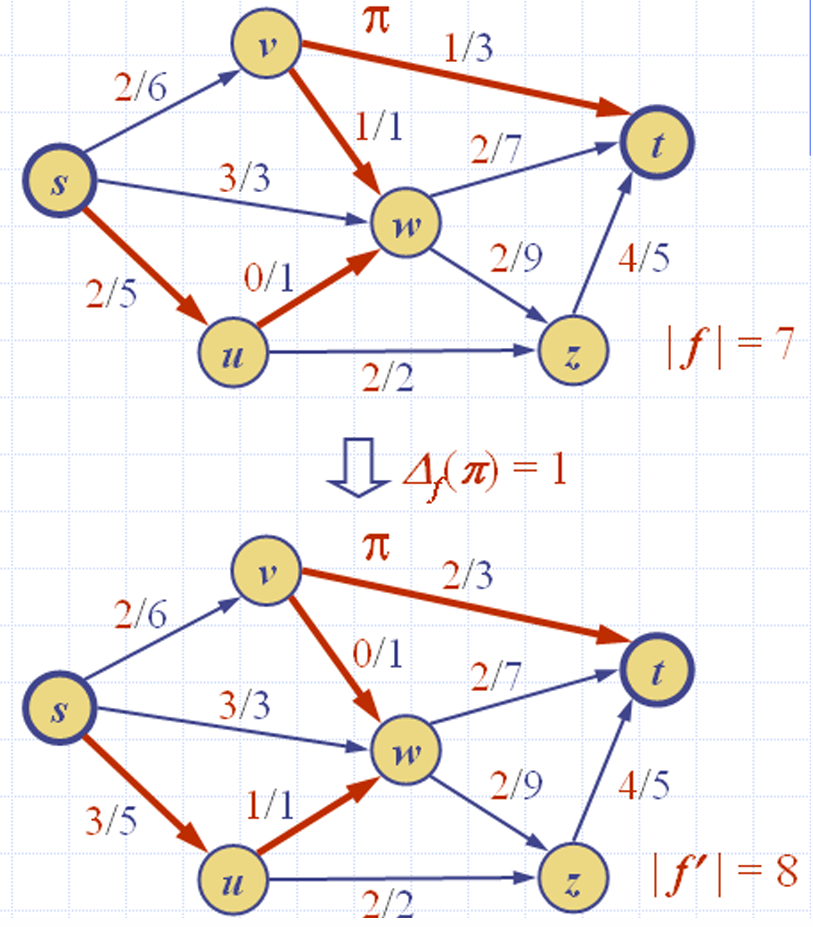
π π π是流 f f f在网络 N N N中的一条增广路径。存在一个流 f ′ f ′ f′对于 N N N,其值为 ∣ f ′ ∣ = ∣ f ∣ + Δ f ( π ) ∣f ′ ∣=∣f∣+Δ f (π) ∣f′∣=∣f∣+Δf(π)。
这也就是流增广。
所以在前面的例子中,我们就可以获得一个更大的流。
5.4最大流最小割定理(Max-Flow, Min-Cut Theorem)/ Ford-Fulkerson 定理( Ford-Fulkerson Theorem)
如果没有增广路径呢?
引理 4(Lemma 4):如果网络 N N N相对于流 f f f没有增广路径,那么 f f f是一个最大流。此外,存在一个割 χ χ χ使得 ∣ f ∣ = c ( χ ) ∣f∣=c(χ) ∣f∣=c(χ)。
根据引理 4和 定理 1我们获得了最大流最小割定理(Max-Flow, Min-Cut Theorem)或者叫 Ford-Fulkerson 定理。
定理 2:最大流的值等于最小割的容量。
我们现在队割(Cut)的结构进行更明确的定义:
V s V_ s Vs是从源点 s s s通过增广路径可达的顶点集。
V t V_t Vt是剩余的顶点集,即 V t = V − V s V_t =V−V_s Vt=V−Vs。
割 χ χ χ是将顶点集 V V V分成 V s V_s Vs和 V t V_t Vt的划分,所以现在 c ( χ ) = ∣ f ∣ c(χ) = |f| c(χ)=∣f∣,因为前向边中流量 f ( e ) = c ( e ) f(e)=c(e) f(e)=c(e),而后向边中流量 f ( e ) = 0 f(e)=0 f(e)=0。
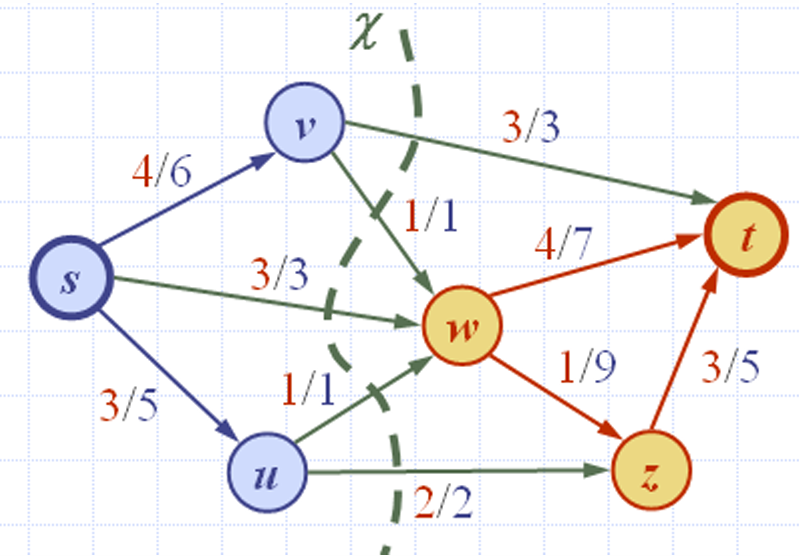
因此现在流 f f f有了最大值,而割 χ χ χ有最小的容量,即 c ( χ ) = ∣ f ∣ = 10 c(χ) = |f|=10 c(χ)=∣f∣=10。
5.5 Ford-Fulkerson 算法
我们现在介绍 Ford-Fulkerson 算法用于解决最大流问题。
算法步骤如下:
首先,将图中每条边的初始流量 f ( e ) f(e) f(e)设为 0 0 0。
然后重复执行以下操作,直到没有增广路径为止:
在残余网络中寻找一条从源点 s s s到汇点 t t t的增广路径 π π π,然后找到增广路径 π π π上的最小残余容量 Δ f ( π ) Δf(π) Δf(π)。瓶颈容量是路径上所有边的残余容量中的最小值,即 Δ f ( π ) = m i n r e s i d u a l c a p a c i t y ( e ) , e d g e e ∈ π Δf(π)= min residual capacity(e),edge \ e∈π Δf(π)=minresidualcapacity(e),edge e∈π。
沿着增广路径 π π π增加流量,增加的量等于瓶颈容量 Δ f ( π ) Δf(π) Δf(π)。
对于前向边(从 V s V_s Vs到 V t V_t Vt的边),流量增加 Δ f ( π ) Δf(π) Δf(π)。对于后向边(从 V t V_t Vt 到 V s V_s Vs的边),流量减少 Δ f ( π ) Δf(π) Δf(π)。
下面给出一个例子。
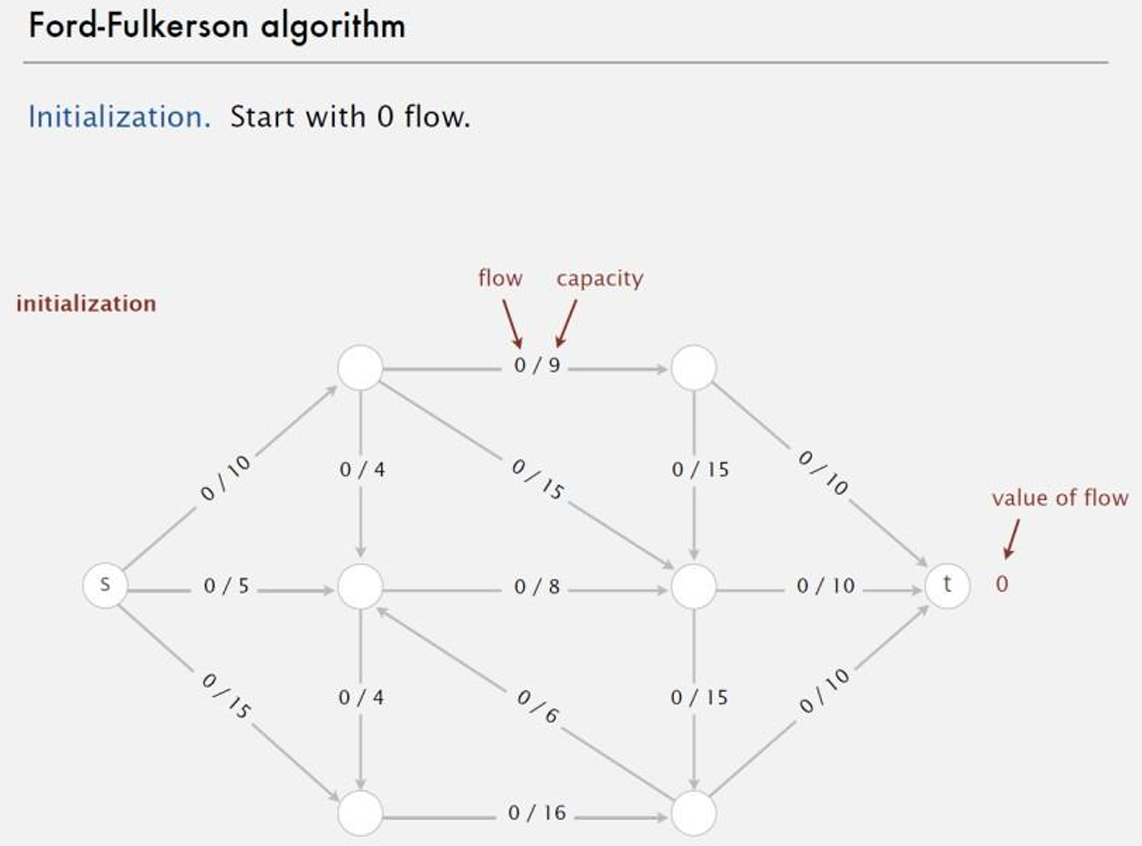
第一步将图中每条边的初始流量 f ( e ) f(e) f(e)设为 0 0 0。
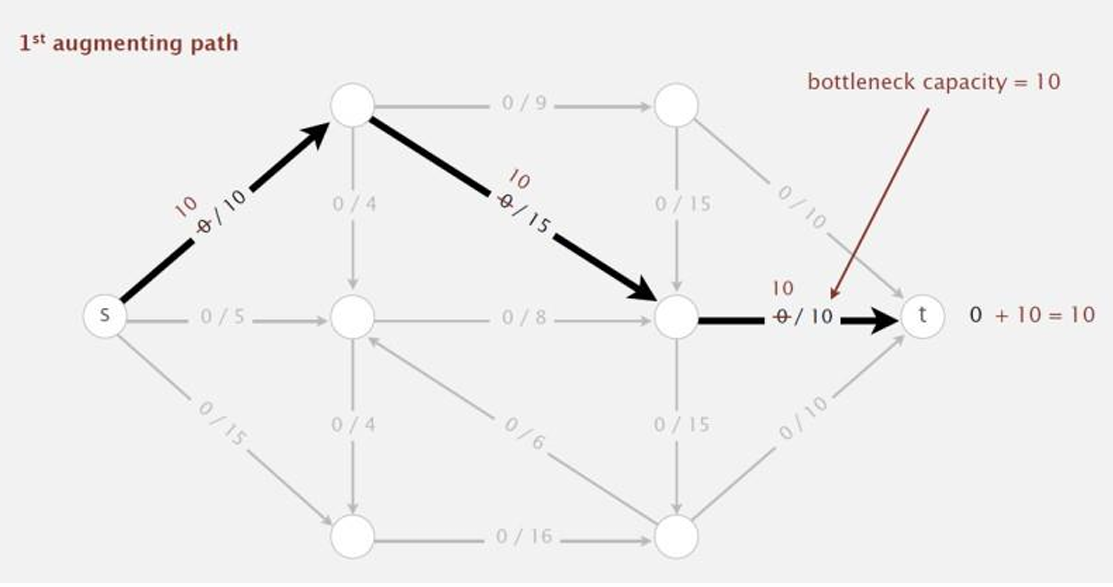
第二步,我们选择一条增广路径,沿着这条增广路径 π π π增加流量,增加的量等于瓶颈容量 Δ f ( π ) Δf(π) Δf(π)。

然后我们再选择一条增广路径,沿着这条增广路径 π π π增加流量,增加的量等于瓶颈容量 Δ f ( π ) Δf(π) Δf(π)。

由于还有增广路径,我们再选择一条增广路径,沿着这条增广路径 π π π增加流量,增加的量等于瓶颈容量 Δ f ( π ) Δf(π) Δf(π)。

我们继续重复这个过程。
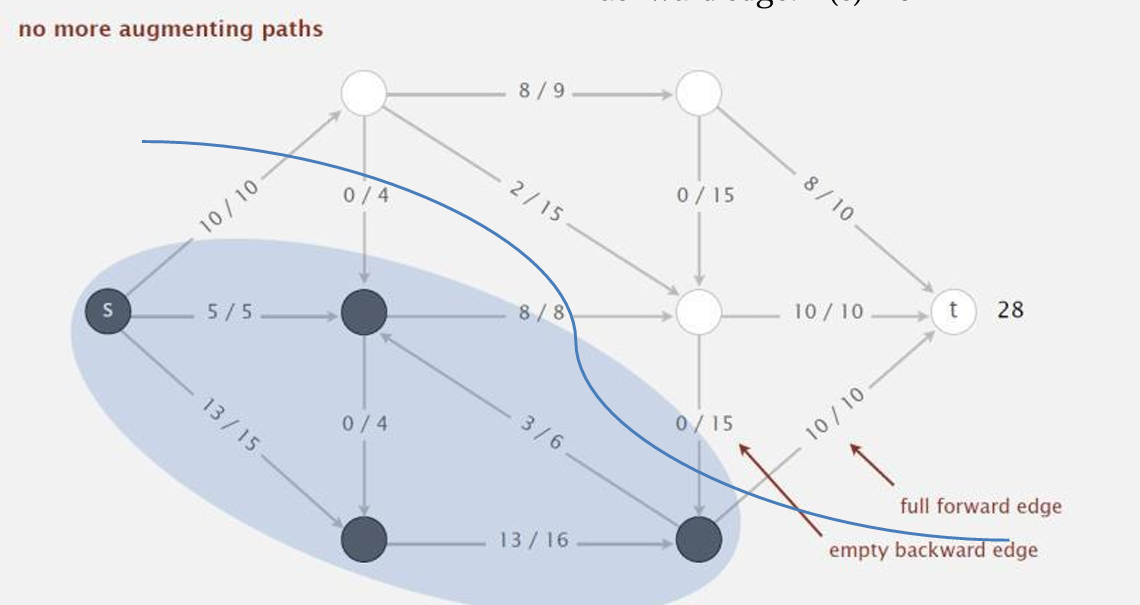
至此,没有增广通路了,所以我们就找到了最大流。
这时如图所示,割的结果满足前向边中流量 f ( e ) = c ( e ) f(e)=c(e) f(e)=c(e),而后向边中流量 f ( e ) = 0 f(e)=0 f(e)=0。
6. 二分图匹配(Bipartite Matching)
现在我们进入下一个概念,二分图匹配。
二分图(Bipartite Graph):如果一个图 G = ( V , E ) G=(V,E) G=(V,E)的顶点集 V V V可以被分成两个不相交的子集 X X X和 Y Y Y,并且图中的每条边都有一个端点在 X X X而另一个端点在 Y Y Y(即图中不存在连接 X X X内或 Y Y Y内的边),那么这个图被称为二分图。
匹配(Matching):一个匹配 M ⊆ E M⊆E M⊆E是边的一个子集,满足以下条件:
1.没有两条边共享一个公共顶点。
2.每个顶点从其中一个集合最多有一个“伙伴”在另一个集合中。
暴露/未匹配顶点(Exposed/Unmatched Vertex):如果顶点 v v v没有 M M M中的边与之相邻,那么 v v v被称为暴露的(或未匹配的)。
完美匹配(Perfect Matching):如果一个匹配覆盖了所有顶点(即不存在暴露顶点),那么这个匹配被称为完美匹配。
下面给出例子。
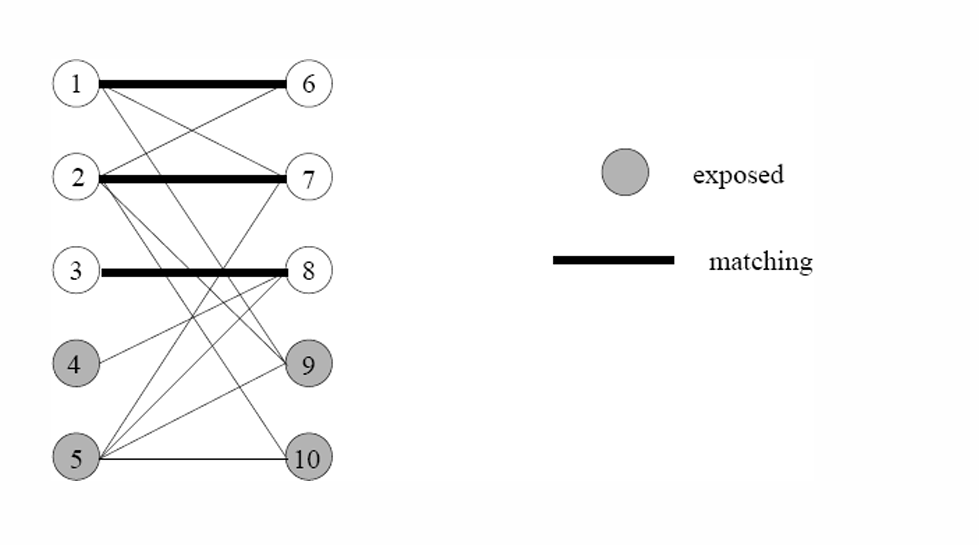
如图所示是一个二分图,因为左右顶点为两个不相交的子集。而我们取出部分的边出来就是一个匹配。在这个匹配下有 4 4 4个点没有匹配上,所以它们是暴露的(或未匹配的)。
所以最大二分图匹配问题的目标是找到一个匹配 M M M,它包含尽可能多的边。换句话说,我们希望最大化匹配中的边数。
6.1 最大二分图匹配问题(Maximum Bipartite Matching)
最大二分图匹配问题(Maximum Bipartite Matching):给定一个二分图 G = ( A ∪ B , E ) G=(A∪B,E) G=(A∪B,E),其中 A A A和 B B B是两个不相交的顶点集, E E E是连接 A A A和 B B B中顶点的边的集合。目标是找到一个匹配 S ⊆ A × B S⊆A×B S⊆A×B,使得 S S S中的边数尽可能多。
注意两点:
- 问题中已经给出了集合 A A A和 B B B,不需要我们自己找到它们。
- 如果匹配 S S S中的每个顶点都被匹配了,即 A A A中的每个顶点都与 B B B中的一个顶点相连,反之亦然,那么这个匹配被称为完美匹配(Perfect Matching)。
下面给出一些例子。
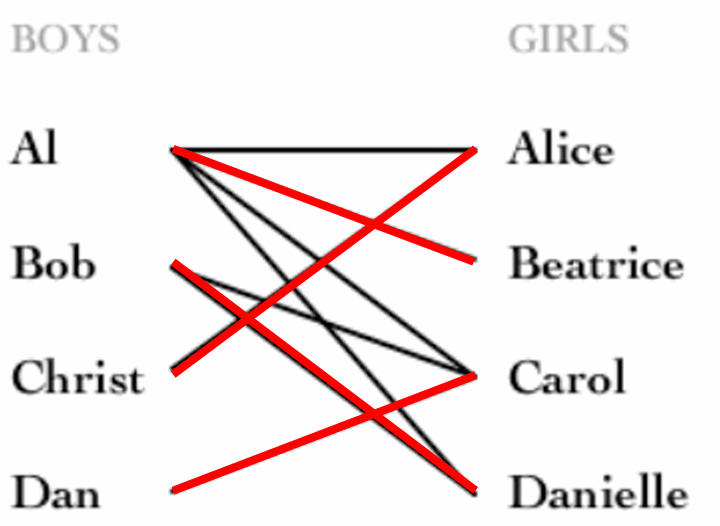
例1:设图 G G G是一个二分图,其中顶点集 X X X代表一组男孩,顶点集 Y Y Y代表一组女孩。每条边连接 X X X中的一个男孩和 Y Y Y中的一个女孩,表示这两个人愿意一起跳舞。
最大二分图匹配问题便是在图 G G G中寻找一个最大的匹配 M M M,即找到最多的配对方式,尽可能使得每个男孩和一个女孩都能形成一对愿意一起跳舞。
例2:设图 G G G是一个二分图,其中顶点集 L L L代表一组人,顶点集 R R R代表一组工作。每条连接 L L L和 R R R的边表示这个人能胜任这个工作。
最大二分图匹配问题便是在这种情况下,我们希望找到一个匹配,使得尽可能多的人能够被分配到他们能够胜任的工作中。
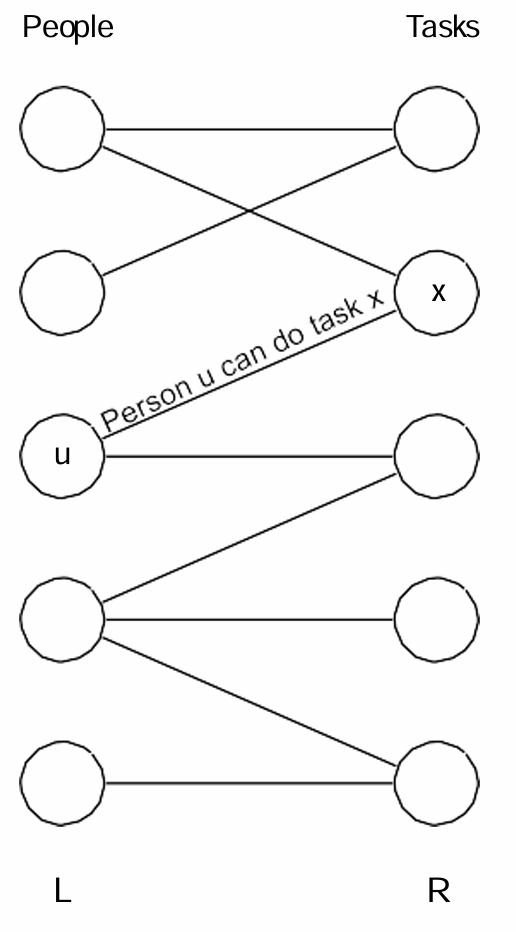
我们对这个例子进行更细致的讨论。
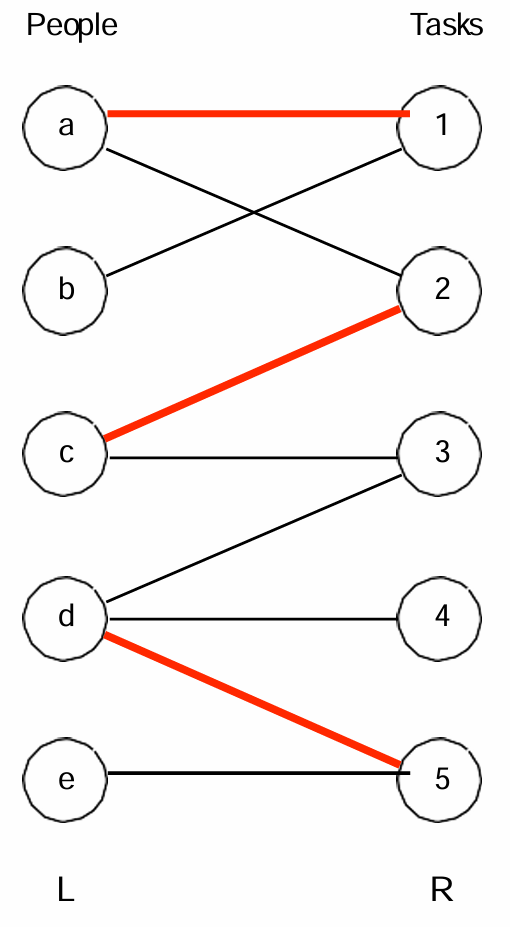
如上图, ( a , 1 ) , ( c , 2 ) , ( d , 5 ) (a,1), (c,2),(d,5) (a,1),(c,2),(d,5)是匹配的,而 b , e , 3 , 4 b,e,3,4 b,e,3,4是暴露/未匹配顶点。

如上图,现在的匹配是完美匹配,因为覆盖了全部顶点。
当然最大匹配可能不是唯一的,如下图所示。
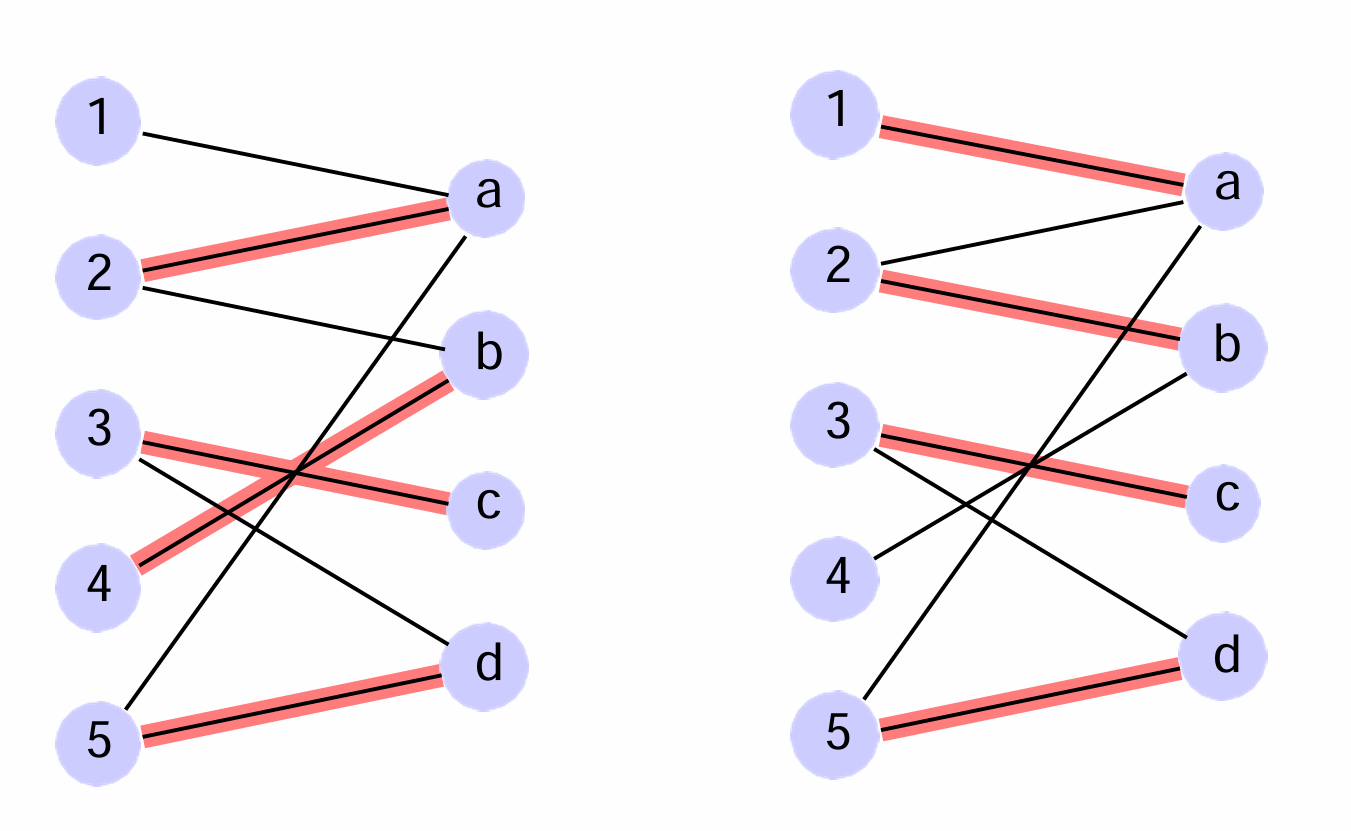
我们其实可以将最大二分图匹配问题转化为网络流问题,并使用网络流方法来解决它。
转化步骤如下:
- 确保边的方向:首先确保所有从集合 U U U到集合 V V V的边都是有向的。
- 引入源点 X X X:引入一个单一的源点 X X X,该点有指向集合 U U U中每个节点的出边。
- 引入汇点 Y Y Y:然后添加一个汇点 Y Y Y,该点有来自集合 V V V中每个节点的入边。
通过上述转化,最大二分图匹配问题现在变成了在图中寻找最大流的问题。
如下图所示。
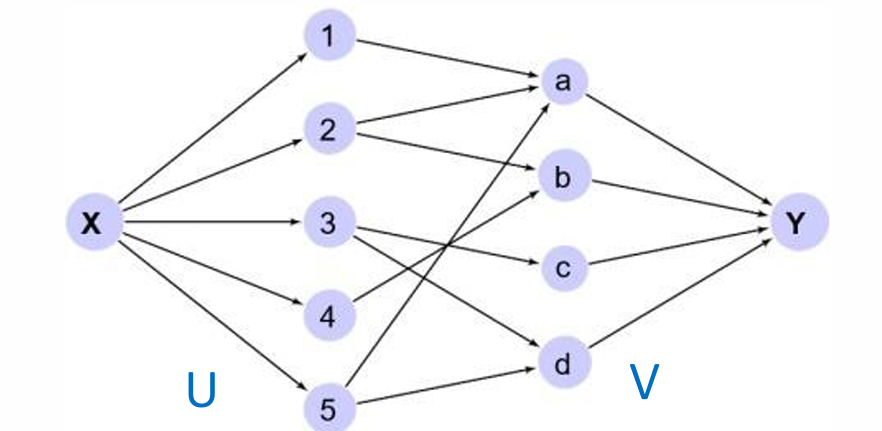
我们可以将网络流问题直观地理解为水通过管道流动,其中管道代表图中的边。
虽然我们有很多算法可以解决网络流问题,但是对于二分图,我们不需要大多数网络流算法的通用性。我们将二分图匹配问题转化为无权有向图的最大流问题,我们可以利用二分图的特殊结构而使用更简单的算法来解决这个问题。
6.2 最大二分图匹配问题的算法
步骤如下:
- 首先,我们需要构建一个有向图,其中包含源点 s s s和汇点 t t t。源点 s s s连接到集合 U U U中的每个顶点,汇点 t t t连接自集合 V V V中的每个顶点。
- 然后使用搜索方法(如深度优先搜索或广度优先搜索)找到从源点 s s s到汇点 t t t的一条路径。
- 一旦找到路径,将该路径上的所有边反转。这意味着如果原始边是从 U U U到 V V V的,现在它将从 V V V到 U U U。
- 一直重复步骤 2 2 2和 3 3 3,直到找不到从汇点 t t t到源点 s s s的路径为止。
- 最终的匹配解是那些从 V V V到 U U U的边的集合(即所有被反转的边)。
这个过程实际上是在模拟增广路径(augmenting paths)的过程。
我们以刚刚的那个例子为例。
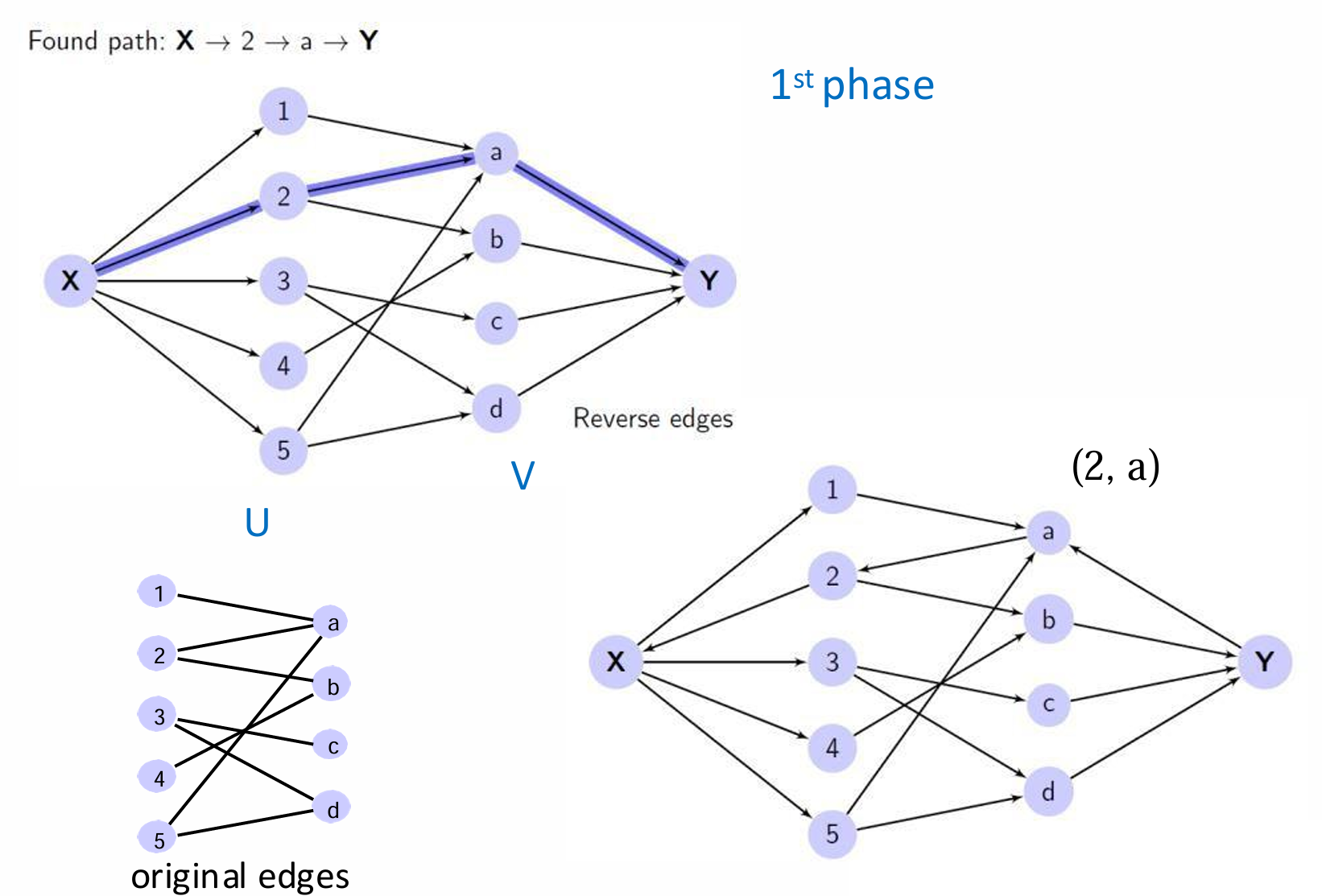
我们找到路径就将该路径上的所有边反转。

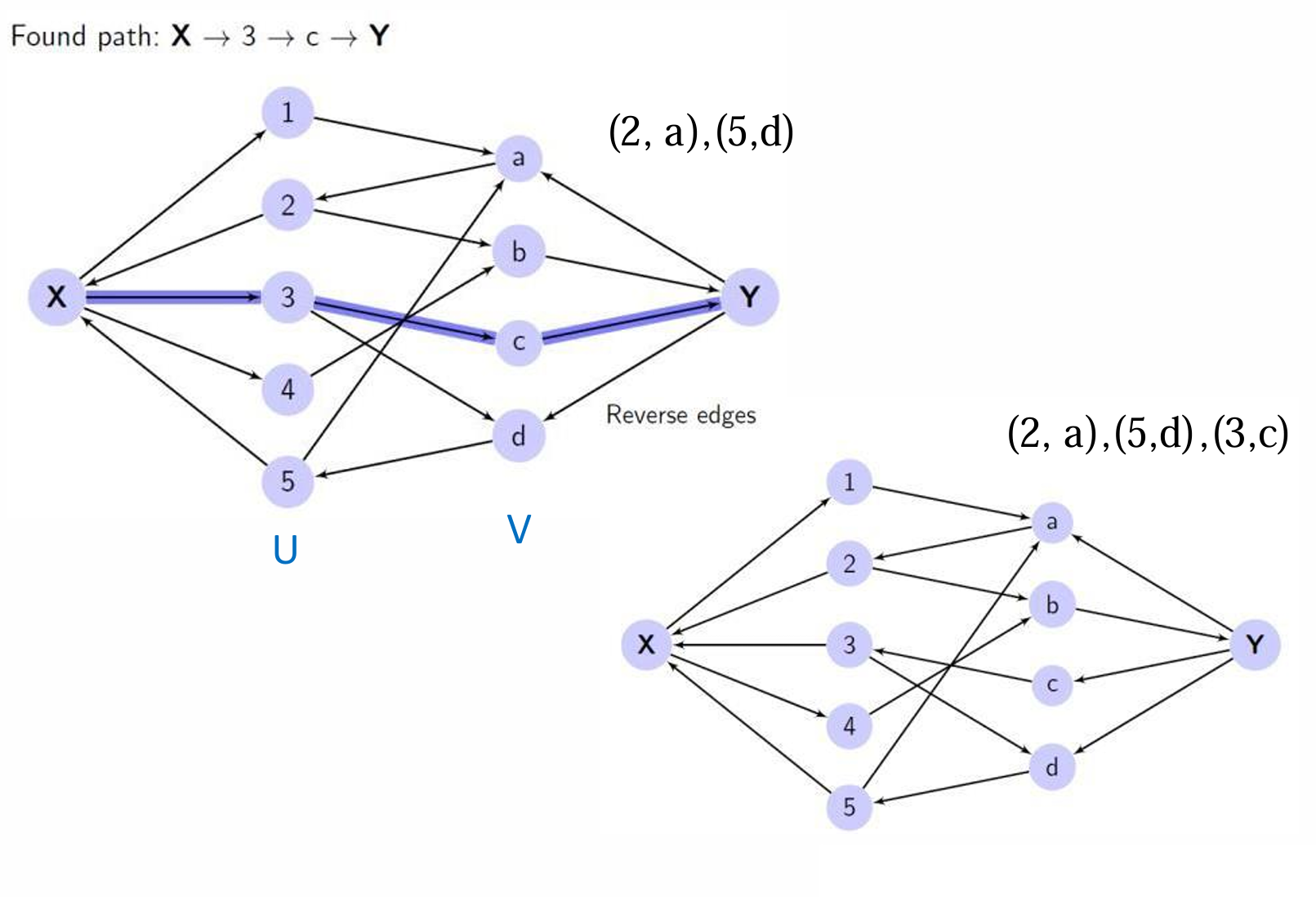
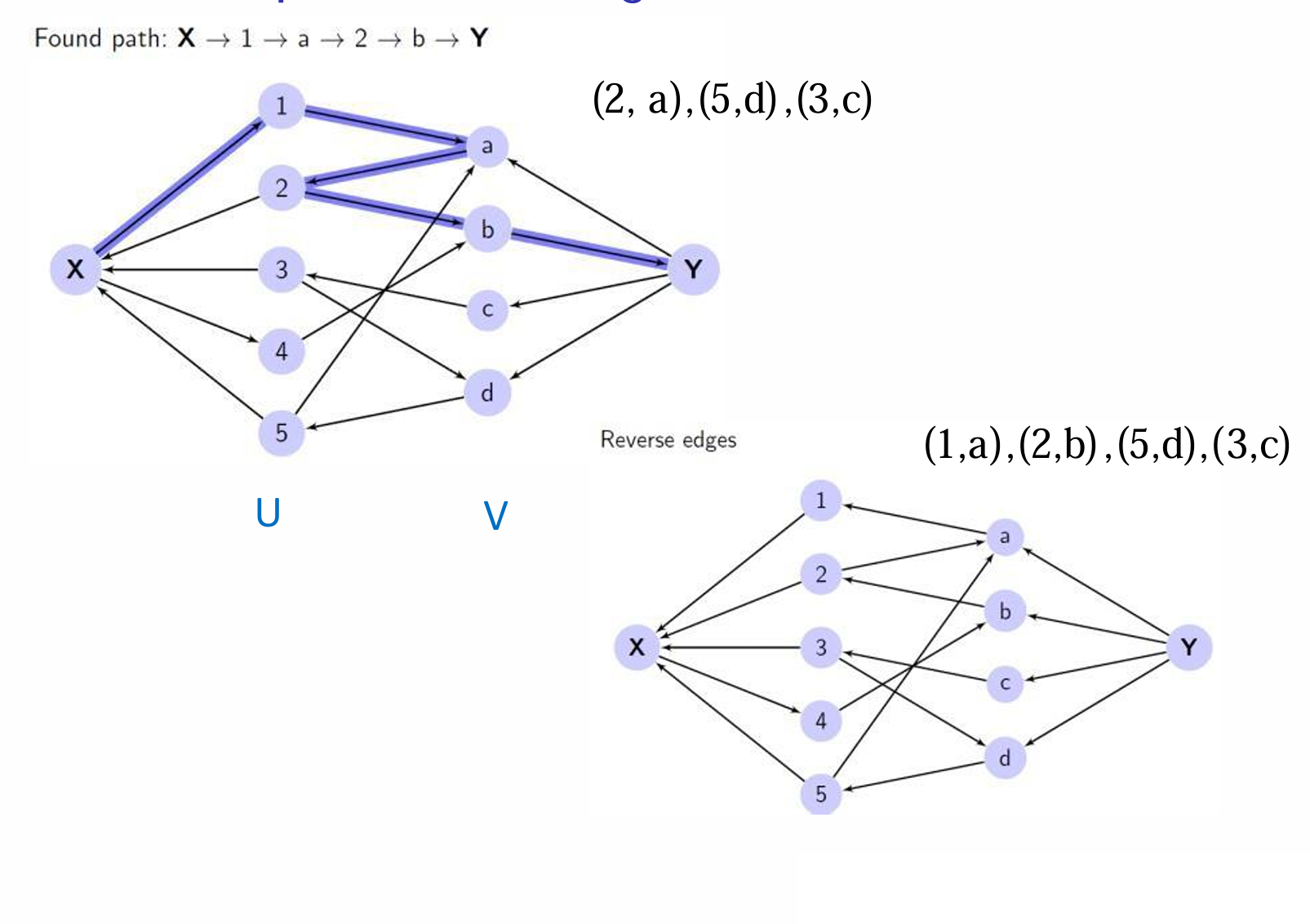
一直重复这个过程。
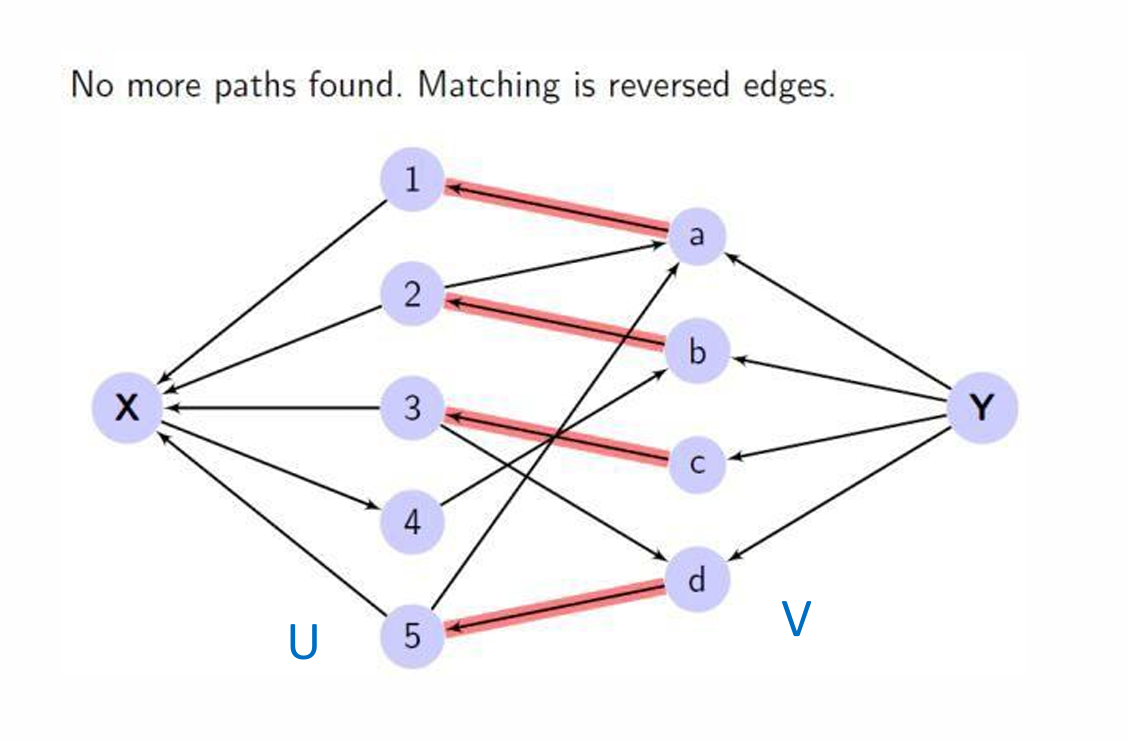
找不到符合的路径便得到了最终的结果,如图中红线所示。



![[C++] STL数据结构小结](http://pic.xiahunao.cn/nshx/[C++] STL数据结构小结)



