【CF】Day54——Educational Codeforces Round 161 (Rated for Div. 2) DE

D. Berserk Monsters

题目：

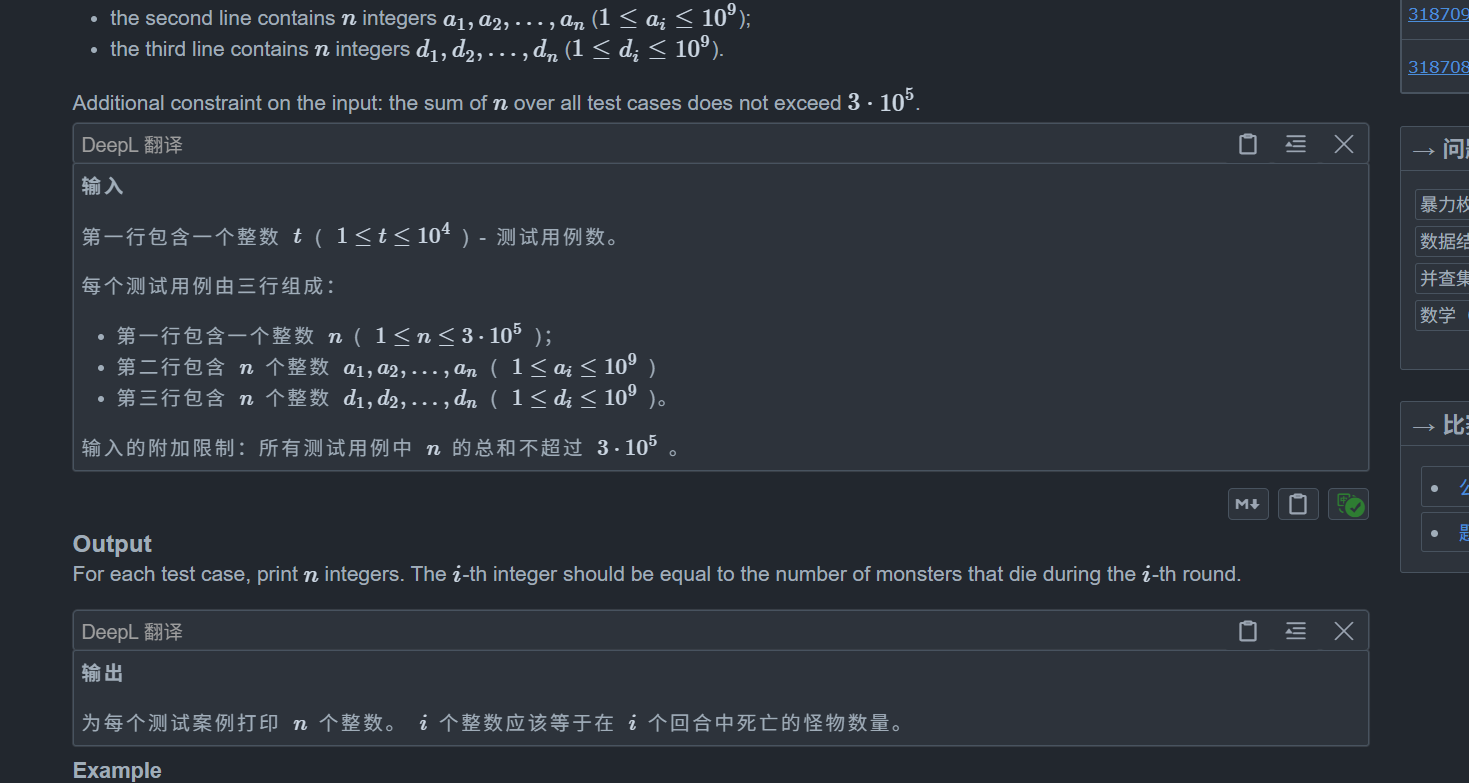
思路：

考优化

这题复杂度很迷，但均摊下来大概是 O(n)

这题没什么思维，但是很需要优化，首先我们可以直接模拟一遍，但是如果没考虑优化的话我们就会超时

我们从两个点上考虑，第一我们考虑如何快速获取一个怪物左右两边的怪物，如果我们使用vector模拟，那我们可以考虑使用erase来删除元素，这样只需要读取 i -1 和 i + 1 即可，但是由于每次删除都要重新排，所以时间复杂度是很大的，因此我们可以考虑另一种数据结构，这种要获取左右元素的情况我们能想到什么呢？答案肯定是链表

我们可以像链表一样使用Left和Right来存储一个元素的左右元素，这样更新和读取就都是O(1)的复杂度了，那么这样就解决了快速更新问题

但是我们发现这样还是不能过，为什么呢？

我们可以想到一个情况，如果一个 x ，他这回合没死掉，并且 x - 1 和 x + 1 都没死掉，那么下回合这个 x 肯定不会死掉，所以这种情况如果有很多的话我们就会又重复考虑，所以我们可以用一个set来存储下一回合应该判断哪些怪物需要判断，同时还需要存储一个 live 数组，判断哪些怪物死了，最后还需要一个set来判断这回合有哪些怪需要被清除

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"const int MAXN = 3e5 + 5;
int a[MAXN], d[MAXN], Left[MAXN], Right[MAXN],live[MAXN];
int n;void solve()
{cin >> n;//vector<int> a(n + 2), d(n + 2), left(n + 2, -1), right(n + 2, n + 1);set<int> alive,del;for (int i = 1; i <= n; i++){cin >> a[i];alive.insert(i);live[i] = 1;}for (int i = 1; i <= n; i++){cin >> d[i];Left[i] = i - 1;Right[i] = i + 1;}Left[1] = Right[n] = 0;while (n--){for (auto i : alive){if (a[Right[i]] + a[Left[i]] > d[i])del.insert(i),live[i] = 0;}cout << del.size() << " ";alive.clear();for (auto i : del){Right[Left[i]] = Right[i];Left[Right[i]] = Left[i];if (live[Left[i]]){alive.insert(Left[i]);}if (live[Right[i]]){alive.insert(Right[i]);}}del.clear();}cout << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(false);int t = 1;cin >> t;while (t--){solve();}return 0;
}

E. Increasing Subsequences

题目：

思路：

思维题，感觉比D题简单

我们要知道一个递增序列他能产生的不包括空集的子递增序列的数量是 $2^{n}-1$

那么观察一下题意，X的最大值是 1e18，也就是我们最多只需要一个 64 长度的子序列就能满足最大值，但是如果 X 不是 2 的整数次幂呢？比如是 2 的 n 次幂减 y，而我们这种构造方法只能解决这种 2 的整数幂的特殊情况，那我们该如何考虑呢？

其实也很巧妙，我们发现一个数能被拆成二进制，而长度为 n 的子序列刚好也能 2 的整数次幂的奉献，所以我们可以考虑将剩余的数拆成二进制来考虑，我们还要发现另一个性质，对于一个已经构造好的数列，如果我们往后添加第 k 大的数，那么增加的奉献就是 2 的 k 次幂（k 从 0 开始）

比如 1 2 3 如果添加 1 ，那就是多了 1，如果添加 2，那就是多了 2 和 1 2，同理 3 也是一样

因此我们的方法也就出来了：先找出最大的小于等于 X 的 2 的整数次幂 k，然后将 x 减去 2 的 k 次幂，并将初始答案按照 1 ~ k 的顺序填入答案数组中，在将剩下的数拆成二进制来从大到小添加数（从大到小添加是为了防止出现 1 2 3 2 3 这种情况，此时新添加的 3 的奉献就不是 2 的 2 次幂了）

由于 X 最大是 1e18，而减去后的最大也不可能超过 1e18，也就是说最多只需要 128 个数就能构造成功，所以是符合题目条件的

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"void solve()
{int x;cin >> x;int n = 0;int now = 1;vector<int> ans;while (now <= x){ans.push_back(n);now *= 2;n++;}ans.pop_back();n--, now /= 2;x -= now;for (int i = 61; i >= 0; i--){if ((x >> i) & 1){ans.push_back(ans[i]);}}cout << ans.size() << endl;for (auto i : ans)cout << i << " ";cout << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(false);int t = 1;cin >> t;while (t--){solve();}return 0;
}