文章目录
- 一. 基本知识
- 1. 线性回归
- 1.1. 基本形式
- 1.2. 线性回归
- 2. 优化方法:梯度下降法
- 2.1. 梯度下降法的直观意义
- 2.2. 随机梯度下降法
- 3. 分类问题
- 3.1. 二分类:逻辑回归-sigmoid函数
- 3.2. 多分类问题--softmax函数
- 4. 岭回归与套索回归
- 4.1. 基础概念
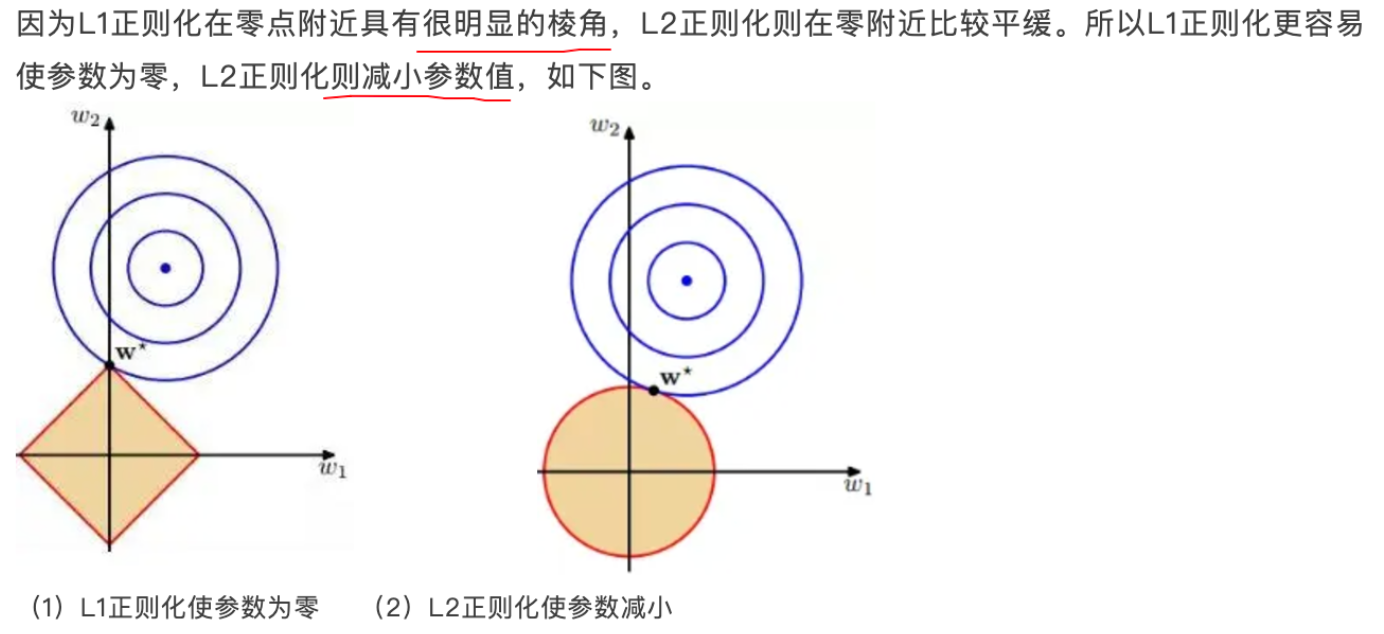
- 什么是正则化
- 范数的概念
- 4.2. 正则化的类型(L1(套索)、L2(岭))
- 4.3. L1、L2的应用
- 岭回归应用例子
- 套索回归应用例子
- 4.4. 普通线性回归、岭回归、套索回归之间的区别
- 5. 支持向量机(SVM)
- 5.1. 完美可分情况
- SVM概念
- 超平面:划分数据的低一维子空间
- 支持向量:确定最优超平面
- 5.2. 不完美可分的情况-核技巧
- 核函数定义
- 核函数类型
- 在支持向量机中的应用
- 二. 课本习题
- 3. 概念题
- 4. 如何限制空间
- 5. 梯度下降的计算
- 6. 随机梯度下降
- 7. Softmax计算
- 8. 岭回归思想
- 9. 套索回归基本思想
- 10. Sigmoid函数
- 11. 岭回归范数
- 12. 计算回归方程
本文主要介绍内容:
掌握数据集、优化、泛化等过程中的方法和存在的问题:
数据集相关
- 数据类型有哪些?(结构化、非结构化的、时间序列等)
- 数据集如何划分?(训练集、验证集、测试集)
- 特征工程有哪些方法和手段?(缺失值、异常值、离散特征编码等)
掌握算法在训练过程中的三要素(模型、目标、优化方法)
机器学习和深度学习模型都是如何优化的?(比如决策树如何确定分割点?神经网络如何训练?)
模型训练过程中存在哪些问题?(欠拟合和过拟合)
怎么判断欠拟合和过拟合?解决过拟合和欠拟合的方法有哪些,是如何实现的?
L1正则和L2正则区别是什么?
优化的目标(损失函数)是怎么选取的?
损失函数有哪些常用函数?表达式以及场景
了解掌握分类与回归的基本原理
了解什么是回归任务,什么是分类任务
分类与回归的常用的损失函数
分类与回归的常用的模型
一. 基本知识
1. 线性回归
1.1. 基本形式
线性模型
线性模型形式简单、易于建模,而且很多更强大的非线性模型都是在线性模型的基础上通过引入层级结构(比如多层感知机模型)或者高维映射(如非线性支持向量机) 得到的,因此线性模型是很多模型学习的基础。
回归任务举例
以回归任务为例,在给定n个属性描述的示例 x = ( x 1 , ⋯ ⋯ x = ( x _ { 1 } , \cdots \cdots x=(x1,⋯⋯ , x _ { n } ),其中的 x i x _ { i } xi是x在第i个属性上的取值,线性模型是最简单的试图通过建立一个属性的线性组来预测的函数,可以表示为: f ( x ) = ω 1 x 1 + ω 2 x 2 + ⋯ + ω n x n + b f ( x ) = \omega _ { 1 } x _ { 1 } + \omega _ { 2 } x _ { 2 } + \cdots + \omega _ { n } x _ { n } + b f(x)=ω1x1+ω2x2+⋯+ωnxn+b
更一般化的向量形式可表示为: f ( x ) = ω T x + b f ( x ) = \omega ^ { T } x + b f(x)=ωTx+b
其中 ω = ( ω 1 , ⋯ ⋯ , ω n ) \omega = ( \omega _ { 1 } , \cdots \cdots , \omega _ { n } ) ω=(ω1,⋯⋯,ωn),ω和b通过学习得到之后,模型也就确定了。
1.2. 线性回归
线性回归(Linear Regression)用于建立一个或多个自变量(解释变量)与因变量(响应变量)之间的线性关系模型。线性回归分析的目标是确定自变量对于因变量的影响程度,并用这种关系来预测未来事件。
我们试图找到一个决策边界 f ( x i ) = ω T x i + b 使得 f ( x i ) 无限接近 y i f ( x _ { i } ) = \omega ^ { T } x _ { i } + b使得f ( x _ { i } )无限接近y _ { i } f(xi)=ωTxi+b使得f(xi)无限接近yi,我们常常采用均方误差的方法,来作为回归任务最常用的度量方法。
2. 优化方法:梯度下降法
作用:寻找最优解:
在机器学习模型训练中,它的主要作用是寻找损失函数的最小值。损失函数衡量了模型预测结果与真实结果之间的差异,通过不断调整模型参数来最小化损失函数,从而得到最优的模型参数,使模型能够更好地拟合数据。
算法具体描述
关键词:梯度的反方向、学习率、学习率的调整(以免错过最优解)
算法基本思想: 迭代更新,以到达算法收敛(导数=0,达到迭代次数)。
求最小损失:使用梯度下降法寻找L的最小解
特征:在线性回归问题中,称输入的不同维度为特征。有些特征比较重要,有些不重要。
2.1. 梯度下降法的直观意义
梯度下降法(Gradient Descent)用于寻找函数的最小值。在机器学习中,常用于最小化损失函数(如均方误差、交叉熵等),进而找到最佳的模型参数。

这段距离的长度与L的具体大小有关,L越大,说明函数导数变换速度越快,那么距离越短 L越小,则说明变化速度缓慢,距离越长。
L越小说明变化速度越慢,距离越长。因此,L的大小控制了梯度下降法可以前进的距离。
2.2. 随机梯度下降法
小批和整批
小批过小:会产生比较大噪声,不容易收敛,但收敛速度快。
收敛速度慢,但计算快。
3. 分类问题
3.1. 二分类:逻辑回归-sigmoid函数
线性模型处理分类问题,可以通过构造对数几率函数,也就是我们通常说的逻辑回归,另外还可以采用线性判别分析(LDA)的方法来处理二分类问题。
逻辑回归(Logistic Regression)是一种广泛使用的统计方法,用于处理二分类问题,即因变量是分类的,并且类别只有两个(如是/否,成功/失败,通过/未通过等)。
注意:尽管它的名字中有“回归”二字,但它实际上是一个分类算法。

逻辑回归: 将二分类问题变为两个维度的概率分布 ( f ( x ) , 1 − f ( x ) ) (f(x),1-f(x)) (f(x),1−f(x))
- 使用Sigmoid函数保证输出是一个 [ 0 , 1 ] [0,1] [0,1] 之间的数
- 将Sigmoid函数与线性函数结合,得到一个概率
- 这样便能使用梯度下降法,注意使用复合函数的链式求导。
3.2. 多分类问题–softmax函数
函数定义:
Softmax 在多分类中的作用
- 概率解释: Softmax函数输出的向量(p)中的每个元素 p j p_j pj可以被解释为样本属于第(j)个类别的概率。例如,在一个五分类问题中,如果经过Softmax函数后得到的概率向量为 ( 0.1 , 0.2 , 0.3 , 0.2 , 0.2 ) (0.1,0.2,0.3,0.2,0.2) (0.1,0.2,0.3,0.2,0.2),那么可以理解为这个样本属于第三个类别的概率是(0.3),其他类别的概率依此类推。
- 分类决策: 根据概率进行分类。通常,我们会将样本分类到概率最高的那个类别。在上述例子中,样本会被分类到第三个类别。
- 与损失函数结合:在训练模型时,常常会和损失函数(如交叉熵损失函数)结合使用。
Softmax的性质和优势
- 单调性:Softmax函数是单调递增的。这意味着输入向量中某个元素的增加会导致对应的输出概率增加,这种性质符合我们对概率分配的直观理解。
- 输出归一化:它能够将任意实数向量转换为合法的概率分布,使得输出结果易于解释和用于分类决策。
- 梯度计算方便:在使用梯度下降等优化算法训练模型时,Softmax函数的梯度计算相对简单,有利于模型的高效训练。
- 将向量转换为概率分布
- 所有数为非负,并且相加=1
4. 岭回归与套索回归
4.1. 基础概念
什么是正则化
“正则”(Regularization)是一种用于控制模型复杂度,为了保证泛化性能,防止过拟合的技术手段。正则化通过在模型的目标函数(如损失函数)中添加一个惩罚项来实现对模型复杂度的约束。
这个惩罚项一般是模型复杂度的单调递增函数:模型越复杂,正则化越大。
形象的比喻:
注意:
- 过拟合是指模型过度学习了训练数据中的噪声和细节,以至于在新的数据上泛化能力很差。
- 正则化可以用于回归问题和分类问题。
范数的概念

常见的向量范数类型
4.2. 正则化的类型(L1(套索)、L2(岭))
L1是通过稀疏参数(减少参数的数量)来降低复杂度,L2是通过减小参数值的大小来降低复杂度。
4.3. L1、L2的应用
岭回归应用例子
| 应用领域 | 具体应用情况 |
|---|---|
| 金融领域 | 分析影响股票价格的诸多因素(如公司财务指标、宏观经济数据、行业指数等)间的共线性问题,运用岭回归构建模型预测股票价格走势,助力投资决策。 |
| 推荐系统 | 针对用户特征、产品特征及交互特征等存在的共线性情况,通过岭回归模型预估用户对商品喜好程度,实现精准个性化推荐。 |
| 医学影像处理 | 处理医学影像(像脑部MRI影像的纹理、形状等特征)分析时面临的高维复杂数据,借助岭回归优化相关算法,辅助医生更精准诊断疾病。 |
套索回归应用例子
| 应用领域 | 具体应用情况 |
|---|---|
| 医学研究 | 从众多与疾病相关的指标(例如心血管疾病涉及的年龄、性别、血压等)里,利用套索回归的L1正则化筛选关键因素,构建疾病预测模型辅助防治。 |
| 基因组学 | 面对海量基因表达数据,使用套索回归筛选出和特定生物表型(比如癌症的亚型、预后相关)有关的关键基因,服务癌症精准医疗。 |
| 经济学 | 在众多宏观经济变量(如货币供应量、经济增长率、失业率等)中,依靠套索回归挑选对通货膨胀等经济现象起关键作用的变量,构建预测模型辅助政策制定。 |
4.4. 普通线性回归、岭回归、套索回归之间的区别
- 普通线性回归:
- 简单直接,计算效率高。
- 容易受到多重共线性和过拟合的影响。当自变量之间高度相关或者自变量过多时,模型的稳定性和泛化能力会变差。
- 岭回归:
- 能有效处理多重共线性问题,通过缩小系数来降低模型方差。
- 不会将系数压缩为 0,所以模型包含所有自变量,没有特征选择功能。
- 套索回归:
- 可以进行特征选择,将不重要的自变量系数收缩为 0,使模型更加简洁。
- 由于 L1 正则化的性质,在某些情况下可能会导致模型估计不够稳定,但在特征选择方面有独特优势。
5. 支持向量机(SVM)
5.1. 完美可分情况
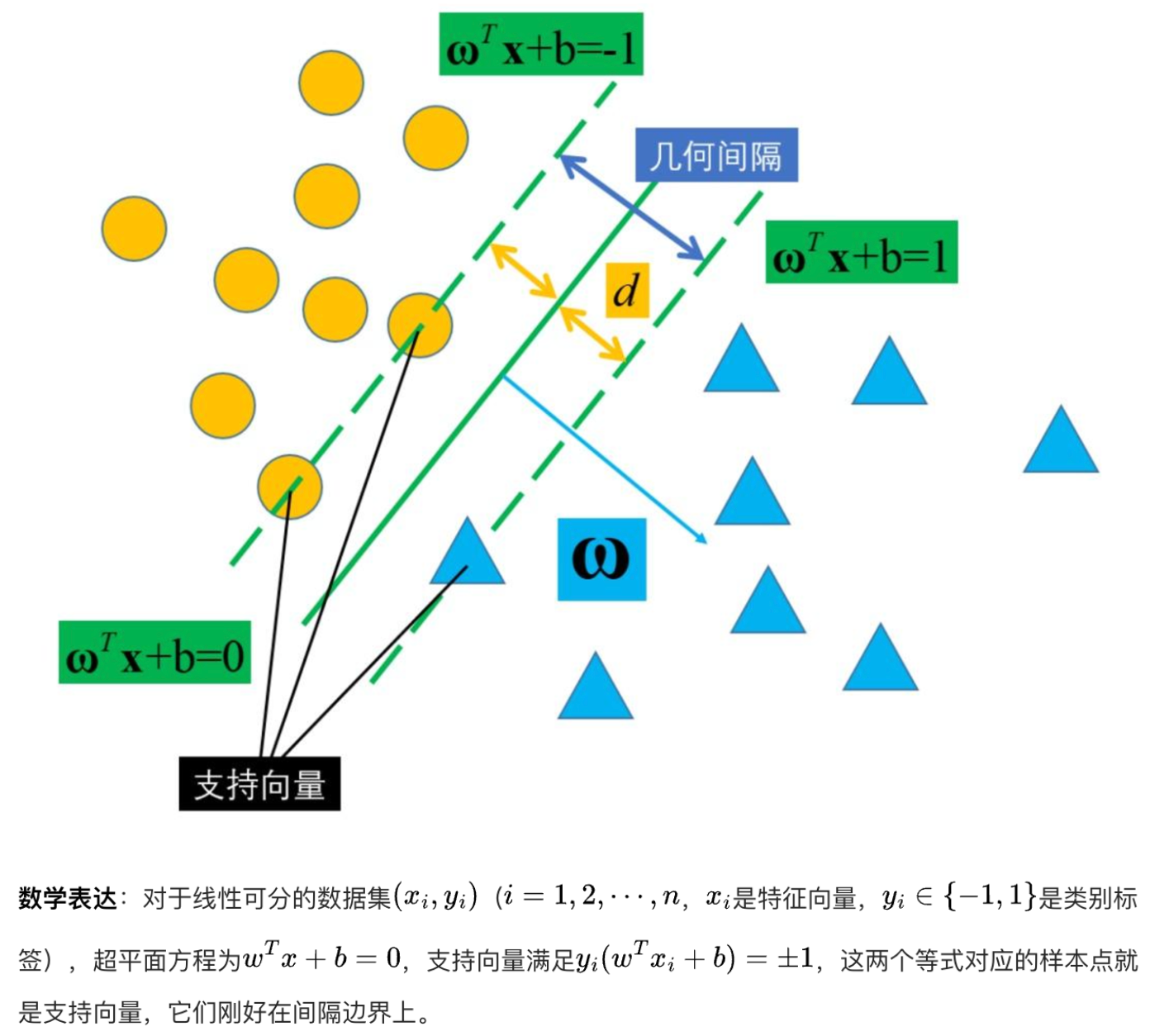
SVM概念
支持向量机是一种监督式学习的分类算法,它的主要目标是在特征空间中找到一个最优的超平面,将不同类别的数据点尽可能清晰地分开。这个超平面被定义为使得两类数据点到它的距离最大化的平面。
超平面:划分数据的低一维子空间
| 方面 | 描述 |
|---|---|
| 定义 | 在高维空间中,是维度比所在空间少一的子空间。二维是直线、三维是平面、n维是n - 1维子空间。可用 w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b = 0 w_1x_1 + w_2x_2+\cdots+w_nx_n + b = 0 w1x1+w2x2+⋯+wnxn+b=0表示,(w)为法向量且垂直于超平面 |
| 性质 | 法向量决定方向,根据点代入方程后的正负判断其位于超平面哪一侧。点(x_0)到超平面的距离为 d = ∣ w ⋅ x 0 + b ∣ ∣ w ∣ d=\frac{\vert w\cdot x_0 + b\vert}{|w|} d=∣w∣∣w⋅x0+b∣ |
| 应用 | 在机器学习分类(如SVM)中作决策边界划分类别;用于数据降维和投影,将高维数据投影到低维超平面上 |
支持向量:确定最优超平面
定义:在支持向量机(SVM)用于二分类问题时,支持向量是位于距离划分超平面最近的那些样本点。这些点对于确定超平面的位置和方向起着关键作用。
在最大间隔超平面中的角色:当数据线性可分,SVM 的目标是找到一个最大间隔超平面将两类数据分开。此时,有两条平行于最大间隔超平面的边界超平面,支持向量就位于这两条边界超平面上。
如下图,在一个简单的二维平面上,两类数据点被一条直线(超平面)划分开,而位于直线两侧最靠近直线且能决定直线位置的点就是支持向量。
重要结论
- 二分类问题,可以使用线性函数作为分类器
- 训练完成后的模型与大部分样本点无关,只与支持向量相关。所以删除不是支持向量的样本点,不会对模型产生影响。
5.2. 不完美可分的情况-核技巧
数据集无法完美的分隔开
- 引入松弛变量,将之前的做错进行软化(将函数间隔加上松弛变量)。
- 惩罚系数
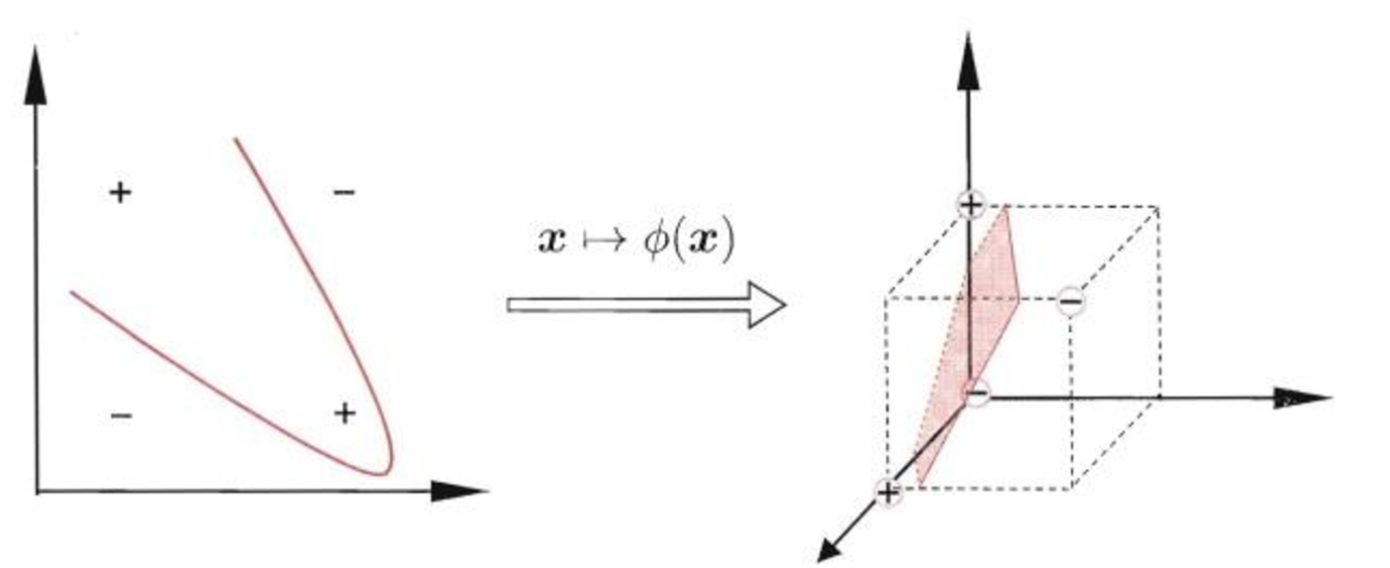
核函数定义
通过一个核函数(Kernel Function)将原始数据隐式地映射到一个高维特征空间,使得在原始空间中线性不可分的数据在高维空间中可能变得线性可分,同时避免了在高维空间中直接进行复杂的计算。
核方法:将点投影到高维空间,就可能用一个线性平面将这些点分开。
核函数类型

在支持向量机中的应用

二. 课本习题
3. 概念题

4. 如何限制空间

1.约束版本
对于线性回归问题,限定参数向量
w的大小,即||w||₂ ≤ c。这里c是一个预先设定的常数,用于限制w的长度。这个约束条件直接对参数向量的长度进行了限制,确保其不会过大或过小。
2.无约束版本min 1 2 N ∣ ∣ X w − y ∣ ∣ 2 2 + λ 2 ∣ ∣ w ∣ ∣ 2 2 \min\frac{1}{2N}||Xw - y||_2^2+\frac{\lambda}{2}||w||_2^2 min2N1∣∣Xw−y∣∣22+2λ∣∣w∣∣22
N是样本数量,X是输入数据矩阵,w是参数向量,y
是目标值向量。这个目标函数由两部分组成:第一部分是均方误差项,表示模型对数据的拟合程度;第二部分是正则化项,通过惩罚参数向量w
的长度来防止过拟合。参数λ用于控制正则化的强度。
通过调整λ的值,可以在拟合数据和限制参数大小之间进行权衡。当λ较大时,正则化项的作用更强,参数向量w会更趋向于零向量,从而防止过拟合;当λ较小时,正则化项的作用较弱,模型更注重拟合数据。例如,在实际应用中,可以通过交叉验证等方法来选择合适的
λ值,以获得最佳的模型性能。
5. 梯度下降的计算

6. 随机梯度下降

在随机梯度下降(Stochastic Gradient Descent,SGD)中,批大小(batch size)对训练过程有着重要的影响,具体如下:
一、批大小较小时的影响
- 随机梯度噪声大:
- 当批大小很小时,每次用于计算梯度的样本数量少。由于样本的随机性,每次计算得到的梯度与使用全量数据计算的真实梯度之间的偏差较大,这就导致了随机梯度的噪声非常大。
- 例如,在图像分类任务中,如果批大小为 1 或 2,那么每个小批次的样本可能具有很大的特殊性,计算出的梯度可能会在不同的方向上剧烈波动,使得模型难以稳定地朝着最优解方向前进。
- 不易收敛:
- 由于随机梯度的噪声大,模型在训练过程中会频繁地在不同方向上进行大幅度的参数更新,难以稳定地收敛到一个较好的解。
- 比如,在回归问题中,小批大小可能导致模型在训练过程中不断地在最优解附近振荡,无法准确地找到最小损失值对应的参数值。
- 此外,小批大小还可能使模型陷入局部最优解,因为在噪声较大的情况下,模型更容易被一些局部的、不稳定的梯度方向所引导。
二、批大小较大时的影响
- 运行速度慢:
- 当批大小较大时,每次参与梯度计算的样本数量多。这虽然可以使计算得到的梯度更接近真实梯度,减少随机梯度的噪声,但同时也会增加计算量和内存占用。
- 例如,在大规模数据集上,如果批大小设置得非常大,可能会导致每次迭代需要花费很长时间来计算梯度,从而使整个训练过程的运行速度变得非常慢。
- 特别是在硬件资源有限的情况下,如内存较小的设备,大的批大小可能会导致内存溢出等问题,进一步影响训练的效率。
- 可能陷入局部最优:
- 较大的批大小可能会使模型在训练过程中过于“平滑”地更新参数,缺乏对不同局部区域的探索能力。
- 这意味着模型可能更容易陷入局部最优解,而错过全局最优解。
- 例如,在复杂的神经网络训练中,大的批大小可能会使模型在某些局部最优解附近停留,而无法跳出该区域去寻找更好的解。
综上所述,在随机梯度下降中,选择合适的批大小非常重要。一般来说,需要根据数据集的大小、硬件资源以及模型的复杂度等因素来综合考虑,以平衡随机梯度的噪声和训练的效率,从而获得更好的训练效果。
7. Softmax计算

8. 岭回归思想

岭回归的基本思想如下:
一、问题背景
在传统的线性回归中,通常使用最小二乘法来求解模型参数,其目标是最小化损失函数 1 2 ∣ ∣ X w − y ∣ ∣ 2 2 \frac{1}{2}||Xw - y||_2^2 21∣∣Xw−y∣∣22,其中(X)是输入数据矩阵,(w)是模型参数向量,(y)是目标值向量。然而,在实际应用中,当数据特征较多或者存在相关性时,普通的线性回归容易出现过拟合的问题。
二、基本思想引入
为了解决过拟合问题,岭回归在普通线性回归的损失函数基础上引入了对参数向量(w)的约束。具体来说,岭回归希望同时限定 ∣ ∣ w ∣ ∣ 2 2 ||w||_2^2 ∣∣w∣∣22(即(w)的长度平方)的大小,要求(w)的长度满足 ∣ ∣ w ∣ ∣ 2 2 ≤ c ||w||_2^2\leq c ∣∣w∣∣22≤c,其中(c)是一个预先设定的常数。这样做的直觉是,通过限制参数向量的长度,可以有效地缩小解空间的大小。
三、作用及意义
- 解决过拟合:限制解空间的大小有助于防止模型过度拟合训练数据。当解空间被限制时,模型不能自由地适应训练数据中的噪声和细微变化,从而减少了过拟合的风险。例如,在高维数据中,可能存在许多特征之间的相关性,而普通线性回归可能会过度依赖某些特征,导致过拟合。岭回归通过限制参数向量的长度,使得模型在选择特征时更加谨慎,从而提高了模型的泛化能力。
- 稳定性提升:对参数向量的约束还可以使模型更加稳定。在数据存在噪声或不确定性的情况下,岭回归可以减少参数估计的方差,使得模型对不同的数据集具有更好的鲁棒性。例如,在实际应用中,数据的采集和测量可能存在误差,岭回归可以帮助模型在面对这些误差时更加稳定地进行预测。
总之,岭回归的基本思想是在普通线性回归的基础上,通过引入对参数向量长度的约束,来解决过拟合问题并提高模型的稳定性和泛化能力。
9. 套索回归基本思想

通过这样的约束,套索回归能够促使模型在众多特征中选择出最重要的一部分特征,将不重要的特征对应的参数设置为零,从而实现特征选择和提高模型的解释性,同时也有助于防止过拟合,提高模型的泛化能力。
10. Sigmoid函数

11. 岭回归范数

12. 计算回归方程

参考:《人工智能基础-姚期智》