经典面试题:接雨水与接雨水II（LeetCode 42与407）

接雨水

问题

给定 $n$ 个非负整数表示每个宽度为 $1$ 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

输入： $h e i g h t = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]$

输出： $6$

解释：上面是由数组 $[0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]$ 表示的高度图，在这种情况下，可以接 $6$ 个单位的雨水（蓝色部分表示雨水）。

解法1：

    public int trap(int[] height) {int length = height.length;int[] maxLeft = new int[length];int[] maxRight = new int[length];int maxTemp = height[0];// 考虑左右方向的最大值,类似前缀和for (int i = 0; i < length; i++) {maxTemp = Math.max(maxTemp, height[i]);maxLeft[i] = maxTemp;}maxTemp = height[length - 1];for (int i = length - 1; i >= 0; i--) {maxTemp = Math.max(maxTemp, height[i]);maxRight[i] = maxTemp;}int ans = 0;for (int i = 0; i < length; i++) {int water = Math.min(maxLeft[i], maxRight[i]);if (water > height[i]) {ans = ans + water - height[i];}}return ans;}

解法2：

    public int trap(int[] height) {int ans = 0;int left = 0, right = height.length - 1;int leftMax = 0, rightMax = 0;while (left < right) {// 将当前的leftMax与rightMax纳入更新氛围leftMax = Math.max(leftMax, height[left]);rightMax = Math.max(rightMax, height[right]);if (height[left] < height[right]) {// 如果height[left]<height[right],那么height[left]肯定比rightMax小// 此时我们只用考虑height[left]于leftMax的比较,但是为什么这样就可以肯定leftMax会比rightMax小// me:因为一旦height[left]<height[right]之后,我们是进行++left希望找到下一个left满足height[left]>height[right]ans += leftMax - height[left];++left;} else {// 此时leftMax会比rightMax大ans += rightMax - height[right];--right;}}return ans;}

接雨水II

问题

给你一个 $m\times n$ 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例 1:

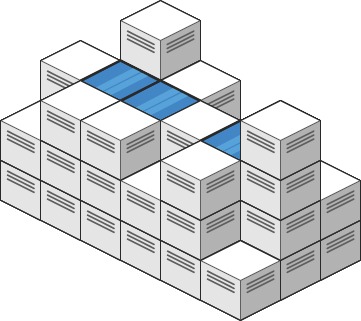
输入: $h e i g h tM a p = [[1, 4, 3, 1, 3, 2], [3, 2, 1, 3, 2, 4], [2, 3, 3, 2, 3, 1]]$

输出: $4$

解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为 $1 + 2 + 1 = 4$ 。

示例 2:

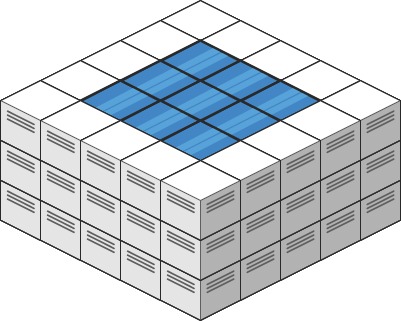
输入: $h e i g h tM a p = [[3, 3, 3, 3, 3], [3, 2, 2, 2, 3], [3, 2, 1, 2, 3], [3, 2, 2, 2, 3], [3, 3, 3, 3, 3]]$

输出: $10$

解法

    public int trapRainWater(int[][] heightMap) {int XLength = heightMap.length;int YLength = heightMap[0].length;// 我们不能像接雨水I版本那样只考虑上下左右的最大值,应该考虑附近的值接完雨水后的最小值// 比如:// 1 4 5 7// 3 1 2 4// 2 3 1 1// 对这数组中的heightMap[1][1]=1,如果我们只考虑4个方向上的最大值,那么应该下Math.min(3,4,4,3)-1=2的雨水// 但是heightMap[1][2]=2是接不了水的,如果让heightMap[1][1]=3,那么他的水会漏出来// 总的来说对应heightMap[i][j],他是受附近的4个点可接的水以及它本身柱的高度所影响的int[] dirs = {-1, 0, 1, 0, -1};// 最大的柱高度int maxHeight = 0;for (int i = 0; i < XLength; i++) {for (int j = 0; j < YLength; j++) {maxHeight = Math.max(maxHeight, heightMap[i][j]);}}// 用于记录最大可能接收的雨水int[][] water = new int[XLength][YLength];for (int i = 0; i < XLength; i++) {for (int j = 0; j < YLength; j++) {// 先接收都接收最大的水water[i][j] = maxHeight;}}Queue<int[]> queue = new LinkedList<>();// 周围边界的柱子肯定是接收不了雨水的for (int i = 0; i < XLength; ++i) {for (int j = 0; j < YLength; ++j) {if (i == 0 || i == XLength - 1 || j == 0 || j == YLength - 1) {if (water[i][j] > heightMap[i][j]) {//  如果他接收了雨水,进行修改,那么他附近的结点也要被进一步修改,因此把这个点放入到队列中water[i][j] = heightMap[i][j];queue.offer(new int[]{i, j});}}}}while (!queue.isEmpty()) {// 如果队列不为空,说明有节点的四周需要被处理int[] curr = queue.poll();int x = curr[0];int y = curr[1];for (int i = 0; i < 4; ++i) {int nx = x + dirs[i], ny = y + dirs[i + 1];// 遍历这个点四周的点if (nx < 0 || nx >= XLength || ny < 0 || ny >= YLength) {// 越界了continue;}if (water[x][y] < water[nx][ny] && water[nx][ny] > heightMap[nx][ny]) {// 如果该节点四周的某一个点比该节点大,并且存放了雨水(water[nx][ny] > heightMap[nx][ny])// 那么这个节点是不合理的// 这个当前节点的周围节点当前接收雨水后的高度为Math.max(当前节点的高度[防止漏水], 这个周围结点本身柱子的高度);water[nx][ny] = Math.max(water[x][y], heightMap[nx][ny]);// 处理了这个(x,y)周围的结点(nx,ny),需要(nx,ny)放进队列中,我们还要处理(nx,ny)四周的节点queue.offer(new int[]{nx, ny});}}}int ans = 0;for (int i = 0; i < XLength; i++) {for (int j = 0; j < YLength; j++) {//water[i][j]-heightMap[i][j]:接收水后的高度-本身柱子的高度ans = ans + water[i][j] - heightMap[i][j];}}return ans;}