高精度激光后向散射建模：从几何重合到光强积分的全流程推导与实现

1. 引言

在激光雷达成像、散射通信、遥感探测等系统中，后向散射（Backscattering） 是信号建模中的关键部分。它涉及了激光束与散射体的空间交汇、能量分布、相函数方向性以及接收器几何响应的复杂耦合过程。

本文围绕典型的后向散射物理场景，推导其核心数学模型，并完成工程实现的剖析。我们最终目标是模拟一个激光发射器—大气路径—目标体—接收器系统在给定时刻的光功率分布。

2. 系统结构与建模对象

模型主要由以下组件构成：

Laser 发射器：具有波束发散角、脉冲宽度、峰值功率等参数；
Path 传播路径：定义大气距离、吸收参数、斜路径角度等；
Target 散射体：分层模拟目标区域的后向散射特性；
Receiver 接收器：具有一定视场角和探测阵列分布；
Other 其它参数：包含发射接收距离、散射层数等；
fieldMode：定义单脉冲（single）或多脉冲（multiple）工作模式。

3. 数学模型推导

3.1 后向散射功率积分基本模型

考虑从发射器出发的激光脉冲在大气中传播，遇到散射体后部分光能量沿不同方向散射。在某个空间体积内，我们对其单位散射能量进行积分：

其中：

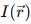：散射中心位置的入射光强；
α：大气吸收系数；
s1,s2：从激光器到体积单元、体积单元到接收器的距离；
：散射相函数，表示散射方向上的能量重分布；
：当前体素中接收视场与发射光束在散射层上的重合面积；
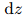：散射层厚度。

3.2 圆形重合面积模型

我们简化模型为两个圆形截面在散射层 zk 上的二维重合问题：

圆1（接收视场）：圆心为 (x1,y1)，半径 r1
圆2（发射光斑）：圆心为 (x2,y2)，半径 r2

两圆心距离为，重合面积的表达式如下：

若圆完全包含：取小圆面积
若部分重合，使用交叉扇形公式：

该部分代码通过三种判断条件精细处理了不同的重合场景，确保结果物理合理且数值稳定。

3.3 光强分布函数 I(r)

我们假设激光束为高斯分布，其在任意传播距离 z上的光斑半径为：

其中为瑞利长度。光强分布：

3.4 时间相关项和层厚估计

我们按时间戳 t对应激光脉冲传播深度 z建立模型：

为了支持多脉冲重叠，需要计算对应时间范围内该层被哪些脉冲覆盖，从而估计有效脉冲数量，进而得到等效层厚Δz。

4. 核心代码实现剖析

4.1 重合圆心坐标计算

代码中圆心坐标如下计算：

posUnitX2 = posUnitX / (path->distance * 1000) * temp2; posUnitY2 = posUnitY / (path->distance * 1000) * temp2;

这是将接收器视场点“投影”到第 k层散射截面 zk上，得到其在该截面上的空间坐标。

发射圆心在该层上的位置为：

cenDis = sqrt( (posUnitX2 + (path->distance * 1000 - temp2) * tan(las->angV))^2 + posUnitY2^2 );

其中平移项显式反映了发射光轴相对于接收器的偏移。

4.2 重合面积判断

if (rRcv + rLas > cenDis) {if (rRcv + cenDis <= rLas) {area = M_PI * rRcv * rRcv;rforI = cenDis;} else if (rLas + cenDis <= rRcv) {area = M_PI * rLas * rLas;rforI = rLas / 2;} else {// 部分重合alpha = acos(...);beta = acos(...);area = (alpha - sin(alpha)*cos(alpha)) * rRcv^2 + (beta - sin(beta)*cos(beta)) * rLas^2;rforI = (rRcv + rLas)/2;}
}

这段实现了标准几何中“两个相交圆”的面积求解，并选取合理的光强积分半径。

4.3 光强计算和能量累计

最终单元光能为：

result = I00(z_k, time, rforI) *exp(-path->atmAC * (s1 + s2) * 0.001) *temp1 * area * thick;result *= rcv->d * rcv->d;  // 探测器尺寸
result /= 16;               // 几何因子
result /= pow(s1 * 0.001 * s2, 2); // 路径平方衰减
final[i][j] += result * path->BETAsc; // 累加