文章目录
- 一、Q-learning
- 现实理解:
- 举例:
- 回顾:
- 二、Sarsa
- 和Q-learning的区别
- 三、Deep Q-Network
- Deep Q-Network是如何工作的?
- 前处理:
- Convolution Networks
- Experience Replay
一、Q-learning
是RL中model-free、value-based算法,Q即为Q(s,a)就是在某一时刻s (s∈S)状态下采取动作a (a∈A) 能够获得收益的期望,环境根据Agent的动作反馈相应的回报reward。将State与Action构建成一张Q-table来存储Q值,然后根据Q值来选取能够获得最大的收益的动作。
| Q-Table | a1 | a2 |
|---|---|---|
| s1 | q(s1,a1) | q(s1,a2) |
| s2 | q(s2,a1) | q(s2,a2) |
| s3 | q(s3,a1) | q(s3,a2) |
也就是马尔科夫决策过程:每个格子都是一个状态 s t s_t st, π ( a ∣ s ) \pi(a|s) π(a∣s)在s状态下选择动作a的策略。 P ( s ’ ∣ s , a ) P(s’|s,a) P(s’∣s,a) ,也可以写做 P s s ′ a P^a_{ss'} Pss′a为s状态下选择动作a转换到下一状态 s ′ s' s′的概率。 R ( s ’ ∣ s , a ) R(s’|s,a) R(s’∣s,a)表示这一Action转移的奖励。

我们的目标是最大累计奖励的策略期望:
m a x π E [ ∑ t = 0 H γ t R ( S t , A t , S t + 1 ) ∣ π ] max_π E [ ∑ _{t = 0} ^H γ^ t R ( S_t , A_t , S_t + 1 )∣π] maxπE[∑t=0HγtR(St,At,St+1)∣π]
使用了时间差分法TD能够离线学习,使用bellman方程对马尔科夫过程求最优解。
在我们探索环境(environment)之前,Q-table 会给出相同的任意的设定值(大多数情况下是 0)。随着对环境的持续探索,这个 Q-table 会通过迭代地使用Bellman方程(动态规划方程)更新 Q(s,a) 来给出越来越好的近似。

算法是基于贪婪的策略进行选择:

S t e p 4 Step 4 Step4中选择动作a并且执行动作并返回一个新的状态 s ’ s’ s’和奖励r,使用Bellman方程更新 Q ( s , a ) Q(s,a) Q(s,a):

新 Q ( s , a ) = 老 Q ( s , a ) + α ∗ ( 现实 − 估计 ) 新Q(s,a)=老Q(s,a)+\alpha*(现实-估计) 新Q(s,a)=老Q(s,a)+α∗(现实−估计)
现实理解:
在状态s采取行动a到达 s ′ s' s′,但是我们用于决策的Q表并没有实际采取任何行为,所以我们只能使用期望值进行下一个状态 s ′ s' s′各个动作的潜在奖励评估:
- Q-Learning的做法是看看那种行为的Q值大,把最大的 Q ( s ′ , a ′ ) Q(s', a') Q(s′,a′) 乘上一个衰减值 γ \gamma γ (比如是0.9) 并加上到达 s ′ s' s′时所获取的奖励 R(真真实实存在的)
- 这个值更新为现实中的新Q值
举例:
- 一块奶酪 = +1
- 两块奶酪 = +2
- 一大堆奶酪 = +10(训练结束)
- 吃到了鼠药 = -10(训练结束)

S t e p 1 Step 1 Step1 初始化Q表都是0(所有状态下的所有动作)
S t e p 2 Step2 Step2 重复 S t e p 3 − 5 Step3-5 Step3−5
S t e p 3 Step 3 Step3 选择一个动作:向右走(随机)
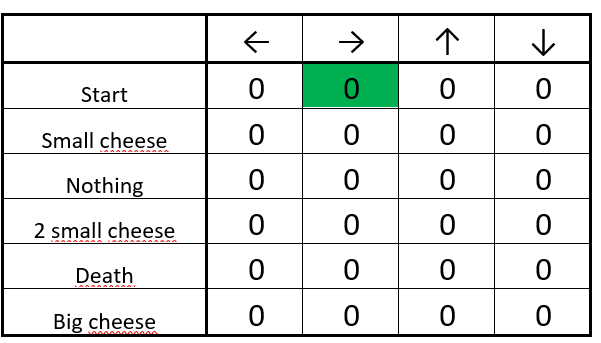
S t e p 4 Step 4 Step4 更新Q函数

- 首先,我们计算 Q 值的改变量 ΔQ(start, right)。
- 接着我们将初始的 Q 值与 ΔQ(start, right) 和学习率的积相加。
回顾:
- Function Q(state, action) → returns expected future reward of that action at that state.
- Before we explore the environment: Q table gives the same arbitrary fixed value → but as we explore the environment → Q gives us a better and better approximation.
二、Sarsa
State-Action-Reward-State-Action,清楚反应了学习更新函数依赖的5个值,分别是当前状态S1,当前状态选中的动作A1,获得的奖励Reward,S1状态下执行A1后取得的状态S2及S2状态下将会执行的动作A2。

和Q-learning的区别
Q_learing:下一步q表最大值 γ ∗ m a x a ′ Q ( s ′ , a ′ ) + r γ*max_{a'}Q(s^′,a')+r γ∗maxa′Q(s′,a′)+rSarsa:具体的某一步估计q值 γ ∗ Q ( s ′ , a ′ ) + r γ*Q(s^′,a^′)+r γ∗Q(s′,a′)+r

Q-learning更激进,当前的Q值和以后的Q都有关系,越近影响越大
Q_learning:取max,也就是不考虑最终走到很大负奖励的值,只考虑会不会最终获得最大奖励,如果获得了,那这条路就牛逼,所以么Q-learning更勇猛,不害怕错,更激进Sarsa:是取某具体的一步,只要周围有错(很大的负奖励),那么就有机会获得这个不好的奖励,那么整条路反馈都会评分很差。之后会尽量避开。那么最终导致Sarsa会对犯错更敏感,会远离犯错的点,更保守
三、Deep Q-Network
成千上万的状态和动作,Q-Table显然不现实。使用Q-Network网络将在给定状态的情况下近似每个动作的不同 Q 值。

Deep Q-Network是如何工作的?

- input: 一组 4 帧
- 为给定状态下每个可能的动作输出一个 Q 值向量
- output:取这个向量中最大的 Q 值来找到我们的最佳行动
前处理:

- 对每个状态进行灰度化,降低state复杂度
- 裁剪帧
- 减小帧的大小,将四个帧堆叠在一起。堆叠?因为它可以帮助我们处理时间限制问题,产生运动的概念
Convolution Networks
使用一个具有 ELU 激活函数的全连接层和一个输出层(具有线性激活函数的全连接层),为每个动作生成 Q 值估计。
Experience Replay
problem1:
- 权重的可变性,因为动作和状态之间存在高度相关性。
- 将与环境交互的顺序样本提供给我们的神经网络。它往往会忘记以前的体验,因为它会被新的体验覆盖。
solution:
- create a “replay buffer.” This stores experience tuples while interacting with the environment, and then we sample a small batch of tuple to feed our neural network.
- 将重播缓冲区视为一个文件夹,其中每个工作表都是一个体验元组。您可以通过与环境交互来喂养它。然后你随机获取一些工作表来馈送神经网络

problem2:
- 每个 action 都会影响下一个 state。这将输出一系列可以高度相关的体验元组。按顺序训练网络,我们的Agent可能会受到这种相关性的影响。
从 replay buffer中随机采样,我们可以打破这种相关性。这可以防止作值发生振荡或发散。
solution:
- 停止学习,同时与环境互动。我们应该尝试不同的东西,随机玩一点来探索状态空间。我们可以将这些体验保存在replay buffer中
- 回忆这些经历并从中学习。之后,返回 Play with updated value function。



)


