最近在做时序预测方面的项目,从零开始一路摸索,也踩了不少坑,终于对这个领域有了一定的了解。在此做一个基本教程,重在概念理解与知识点疏通,帮助对该领域不熟悉的同学快速入门。
由于时序预测任务涉及的知识点较多,我准备用三篇文章分述,分别介绍基础知识、传统方法以及深度学习方法。本篇是该系列的第一篇文章,主要介绍基础知识,要点如下:
- 时间序列
1.1 定义
1.2 基本任务(预测、异常检测等) - 平稳性
2.1 概念
2.2 检验方法(ACF、PACF、假设检验)
2.3 平稳性转换方法
2.4 白噪声 - 评价指标
1. 时间序列
1.1 定义
时间序列(英语:time series)是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。
定义应该很好理解,日常生活中时间序列无处不在:CPU负载、上证指数、商场每天的人流量、商品每日价格。
1.2 基本任务
单指标时序预测任务:给定某一个指标的历史变化情况,预测其在未来一段时间内的变化。
多指标时序预测任务:给定某几个指标的历史变化情况,预测其在未来一段时间内的变化。该任务与单指标时序预测任务的区别在于,几个指标之间不一定相互独立,而是存在某种影响。
时序异常检测任务:从正常的时间序列中识别不正常的事件或行为的过程。可以从历史数据中检测,也可以基于时序预测对尚未发生的异常做出预警。
时序指标聚类:将变化趋势类似的时序指标归至同一类别。在实际运维工作中,面对的指标可能成百上千,分别对其进行分析,工作量太大,可以在聚类的基础上再做建模分析。
指标关联分析:即分析指标A是否会对指标B有影响,以及有什么样的影响(正向/负向、先后关系、多少时间步后造成影响等等)。
2. 平稳性
1.1 概念
平稳性是时序分析的重要概念,时序分析基本上是以平稳时间序列为基础的。
平稳性包括弱平稳与强平稳,其中强平稳的证明很困难。好消息是我们一般不需要关注强平稳,常见的时序分析任务都是基于弱平稳做的。
什么是弱平稳呢?简单来说需要满足以下三点:
- 均值(即从t=0到当前时间步的均值)为常数
- 方差收敛
- 协方差仅与时间间隔有关,与位置无关。
可能有人会好奇,协方差的计算需要两个向量,那么给定一条时间序列,为什么有协方差呢?其实时间序列中的协方差,通过一定间隔的两个时间步的值计算,记间隔为 lag=k,则协方差为 cov(xt,xt−k) 。
2.1 检验方法
常用平稳性检验方法有两种。一种是ACF、PACF图,另一种是假设检验。
2.1.1 ACF、PACF
ACF指自相关性系数,通常用 rk 表示,用于测量时间序列滞后值之间的线性关系,公式如下(可见 r0=1 ):
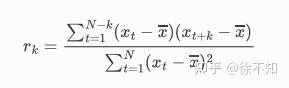
PACF指偏自相关性系数,指剔除了中间k-1个随机变量的影响后, xt−k 对 xt 影响的相关度量。计算较为复杂,这里不介绍了(其实我也没仔细看)。
以时序预测任务中常见的航班数据集为例(AirPassengers.csv,下载点这里),绘图如下:
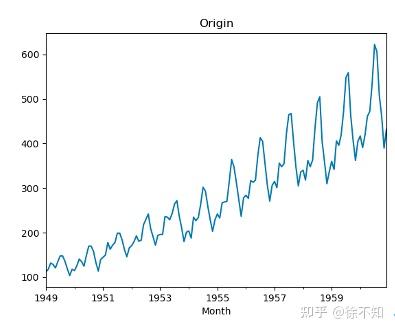
该数据集的自相关函数ACF与偏自相关函数PACF的示意图如下所示,其中横坐标表示间隔为 lag=k,纵坐标表示 rk ,:
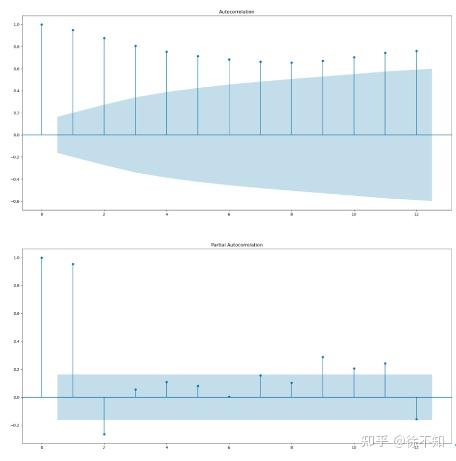
至此关于ACF、PACF的概念介绍结束,那么它们如何作用于平稳性检验呢?对于一个平稳时间序列,自相关系数(ACF)会快速的下降到接近 0 的水平,然而非平稳时间序列的自相关系数会下降的比较缓慢;同样的,非平稳时间序列的自相关系数通常非常大并且为正值。据此,上图中的航班数据集是非平稳的。
我们再举个例子,下图来自于谷歌股价数据集。左图:非平稳;右图:平稳。
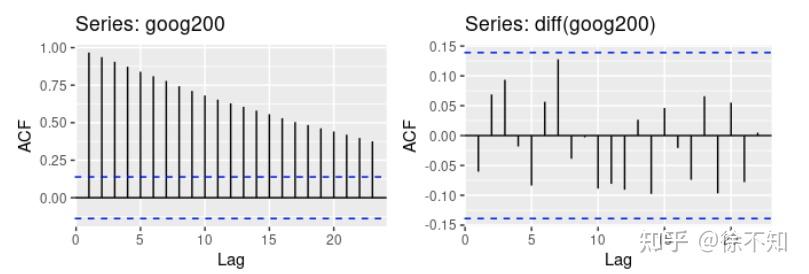
2.2.2 假设检验
常用的用于检测平稳性的假设检验是ADF(Augmented Dickey-Fuller Test)检验,p值小于0.05便可以认为平稳。航班数据集的检验结果如下:

2.3 平稳性转换方法
给定一个非平稳的时间序列,一般需要将它转换为平稳序列,再做建模。常用的平稳性转换方法如下:
- 变形(log函数等)
- 减去移动平均、指数平均等
- 差分
哲理要重点说一下差分。所谓差分,就是用 xt−xt−1 的值代替 xt ,这是一阶差分。在一阶差分的基础上,继续做差分,就是二阶差分。对于大部分时序数据来说,二阶差分后,都可以得到平稳序列,很少用到更高阶的差分。
值得一提的是,对于很多时序预测模型尤其是深度学习模型来说,我们会发现,代码中可能并没有平稳性转换这一步。这是因为这些模型中往往有自动特征提取的步骤,从而隐性地完成平稳性转换。
2.4 白噪声
关于白噪声,网上的描述有很多用词不精准或者相互矛盾之处。我梳理了不少资料,在此将白噪声相关的知识点枚举如下:
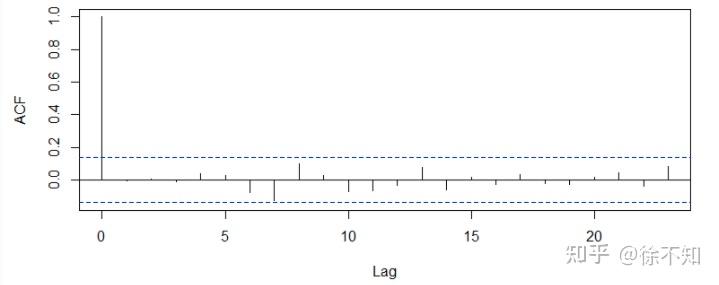
- “白噪声”是一个对所有时间其自相关系数为零的随机过程,如果时序数据是白噪声的话,是没有预测意义的。其ACF图如下(注意 lag=0 时, rk=r0=1 。如果不理解,可回顾2.1.1小节):
- 白噪声和残差完全是两个概念,不要混淆。“残差”在数理统计中是指实际观察值与估计值(拟合值)之间的差。
- 时间序列分解时,残差应该为白噪声才合理。如果不是白噪声,可以考虑对残差继续进行时序建模。时间序列分解会在本系列的下一篇文章中介绍。
- 白噪声是平稳的,但是随机游走(或纯随机序列)并非平稳。“随机游走”指基于过去的表现,无法预测将来的发展步骤和方向。
- 平稳的序列并不一定是白噪声。
- Box-Pierce检验(升级版:Ljung-Box检验)用于判断时间序列是否为白噪声。
3. 评价指标
- RMSE:均方根误差,最常见的一种。
- MAE:平均绝对误差。
- MAPE:平均绝对百分比误差。
- MASE:平均绝对比例误差,这个用得不多。
- R-square:小于0很差,等于0相当于将结果预测为均值,等于1则完全预测正确。这个也比较常见。
- Adjusted R-square:消除了R-square中样本数量的影响。


、地图打印(webprinting)等服务)

——日期类和const成员函数)


