题目
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

代码
关键在于能否想到这个旋转的本质就是
对于矩阵中第 i 行的第 j 个元素,在旋转后,它出现在倒数第 i 列的第 j 个位置。即:matrix_new[col][n-row-1]=matrix[row][col]
然后就是需要注意题目中的原地修改。
但是该方法使用了额外的空间,实际上仍然不符合题目。
方法一:辅助矩阵
class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""n=len(matrix)matrix_new=[[0]*n for _ in range(n)]for row in range(n):for col in range(n):matrix_new[col][n-row-1]=matrix[row][col]matrix[:]=matrix_new#这里使用matrix[:]=matrix_new修改的是matrix本身的内容,也就是原地修改#如果使用matrix=matrix_new修改的只是matrix的指向
方法二:原地旋转
根据图中的方法推出原地旋转过程中数字的交换规律,以及需要主动枚举那些位置的数进行交换
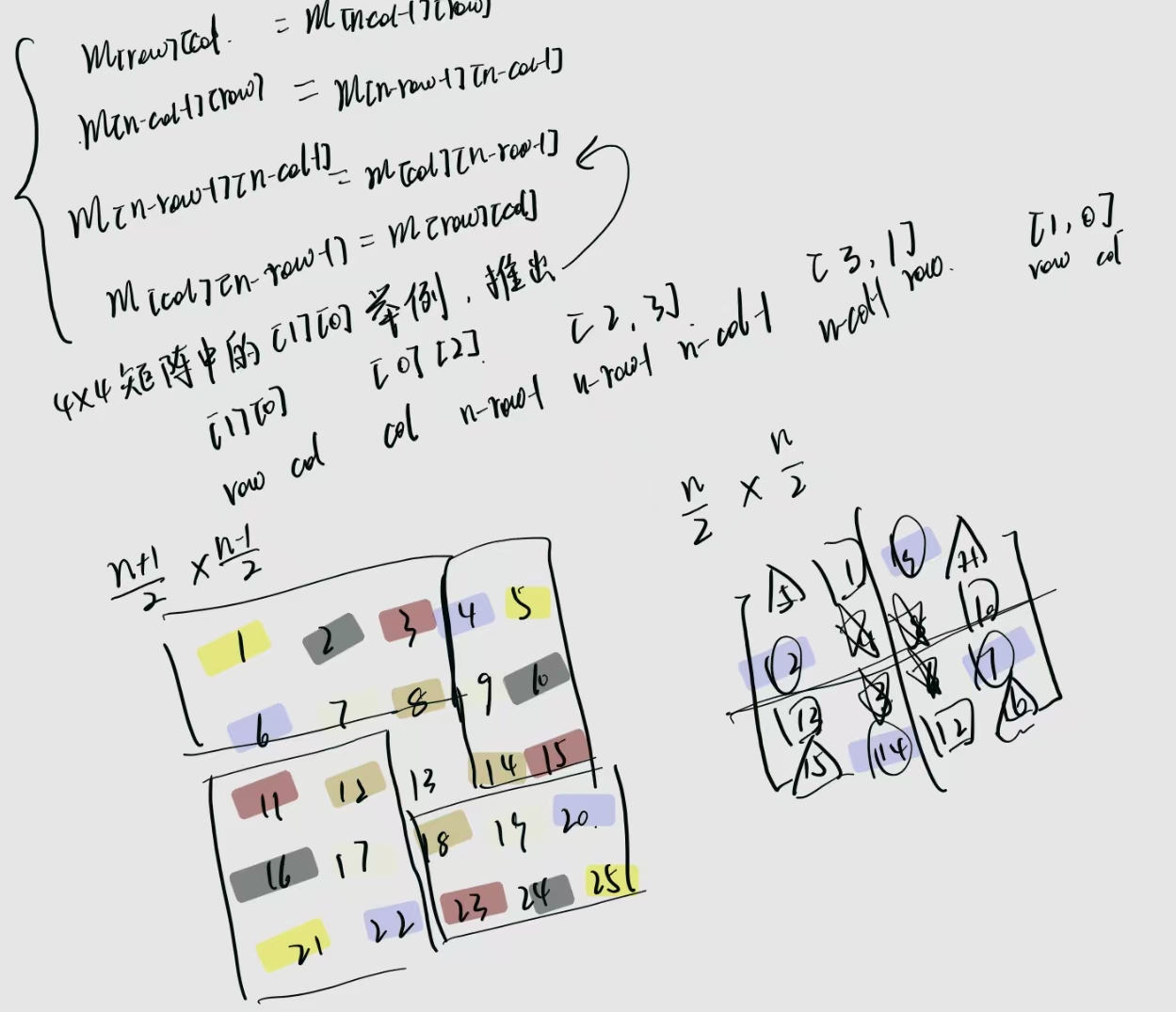
需要注意的是,图中的矩阵的边为奇数和偶数的两种情况,在代码中可以用一种方式实现。
class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""n=len(matrix)for i in range(n//2):for j in range((n+1)//2):matrix[i][j],matrix[n-j-1][i],matrix[n-i-1][n-j-1],matrix[j][n-i-1]=\matrix[n-j-1][i],matrix[n-i-1][n-j-1],matrix[j][n-i-1],matrix[i][j]
方法三:翻转
这里是对矩阵先进行水平翻转再进行主对角线翻转。
只需要注意再代码实现过程中数字遍历,尤其是主对角线翻转的时候
class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""n=len(matrix)# 水平翻转for i in range(n//2):for j in range(n):matrix[i][j],matrix[n-i-1][j]=matrix[n-i-1][j],matrix[i][j]# 主对角线反转for i in range(n):for j in range(i):matrix[i][j],matrix[j][i]=matrix[j][i],matrix[i][j]

)
感知机)


