【算法】5分钟了解如何使用PCA主成份分析

2025/9/13 13:14:49 来源：https://blog.csdn.net/dbat2015/article/details/140065376 浏览: 次关键词：【算法】5分钟了解如何使用PCA主成份分析

本文来自《老饼讲解-BP神经网络》https://www.bbbdata.com/

一、什么是PCA

1.1.PCA的思想

PCA的目的就是去除变量之间的信息冗余，那么PCA是如何处理的呢？
如下，PCA通过旋转样本，使得旋转后的样本每维都互不相关，
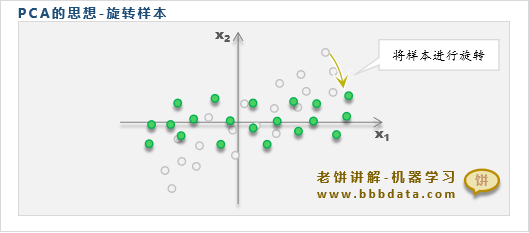
PCA的思想
如此一来样本的相对位置并没有改变，但各维之间互不相关，也就去除了各个变量的信息冗余

1.2.PCA的数学表示

样本的保角保长旋转，在数学上的表示就是一个单位正交变换，即变换前后的样本关系如下：
$X'=(X-\overline{X})A$
其中，A是一个单位正交矩阵，之所以需要减去均值，是为了将样本中心化。

二、什么是PCA的主成份与方差

2.1.主成份的方差

在将样本进行旋转后，得到新的变量X’，X’则称为主成份。
由于主成份之间互不相关，所以可以用每个主成份的方差来代表主成份包含的信息。

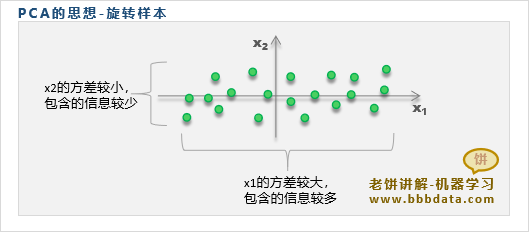
即方差越大，代表该主成份包含的信息越多。

2.2.主成份的命名

主成份的命名
一般地，按方差从大到小，分别称为第一主成份、第二主成份、第三主成份…
第一主成份是方差最大的一个主成份，也代表它包含的信息越多。

三、如何使用PCA

3.1.主成份的代码实现

下面以python为例，实现主成份的计算

# -*- coding: utf-8 -*-
"""
主成份分析求解DEMO(调用sklearn)
本代码来自老饼讲解-机器学习:www.bbbdata.com
"""
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
# 加载数据
iris   = load_iris()    
X      = iris.data       # 样本X
x_mean = X.mean(axis=0)  # 样本的中心 # 用PCA对X进行主成份分析
clf = PCA()   # 初始化PCA对象
clf.fit(X)    # 对X进行主成份分析# 打印结果
print('主成份系数矩阵A:\n A=',clf.components_)
print('主成份方差var:',clf.explained_variance_)
print('主成份贡献占比(方差占比)Pr:',clf.explained_variance_ratio_)# 获取主成份数据
y = clf.transform(X)                # 通过调用transform方法获取主成份数据  
y2= (X-x_mean)@clf.components_.T    # 通过调用公式计算主成份数据

运行结果如下：

主成份系数矩阵A:A= [[ 0.36138659  0.65658877 -0.58202985 -0.31548719][-0.08452251  0.73016143  0.59791083  0.3197231 ][ 0.85667061 -0.17337266  0.07623608  0.47983899][ 0.3582892  -0.07548102  0.54583143 -0.75365743]]
主成份方差var: [4.22824171 0.24267075 0.0782095  0.02383509]
主成份贡献占比(方差占比)Pr: [0.92461872 0.05306648 0.01710261 0.00521218]