欢迎来到尧图网

客户服务 关于我们

您的位置：首页 > 健康 > 养生 > Java八股汇总【Java集合】

Java八股汇总【Java集合】

2025/6/29 15:37:11 来源：https://blog.csdn.net/m0_46427179/article/details/143854702  浏览:  次   关键词：Java八股汇总【Java集合】

1. 集合概述

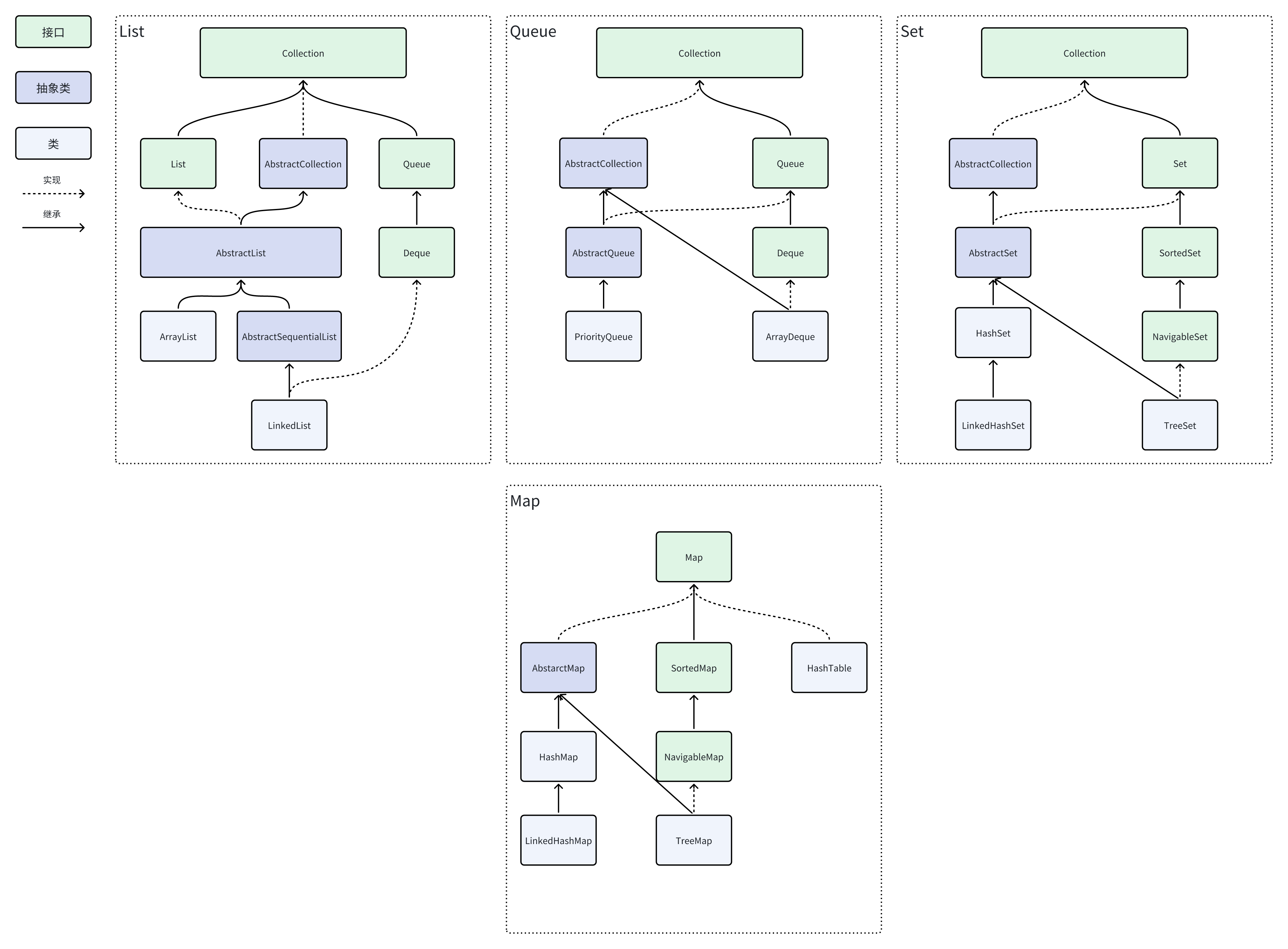
  • Java集合主要可以分为单列集合Collection和双列集合Map

1.1. Collection

  • Collection，可以分为List、Set、Queue三类
    • List，代表有序、可重复的集合
      • ArrayList，动态可扩容数组
      • LinkedList，双向链表，可以当做队列或者栈使用
    • Set，代表不可重复的集合
      • HashSet，通过哈希表实现的无序不重复集合
      • LinkedHashSet，通过哈希表实现的先后有序的不重复集合
      • TreeSet，通过红黑树实现的有序不重复集合
    • Queue，代表有序、可重复、符合某种特定规则的集合
      • PriorityQueue，优先级队列-堆，分为大顶堆，小顶堆，默认为小顶堆
      • ArrayDeque，基于数组的双端队列

1.2. Map

  • Map代表以键值对形式存储的集合，key不能重复，value可以重复
    • HashTable，线程安全的哈希表，但官方更建议使用concurrentHashMap
    • TreeMap，红黑树
    • HashMap，使用红黑树优化后的哈希表
    • LinkedHahsMap，在HashMap的基础上增加了双向链表来保持键值对的插入顺序
      Java集合体系
Java集合体系

2. List

2.1. ArrayList和Array的区别

2.1.1. 可变性

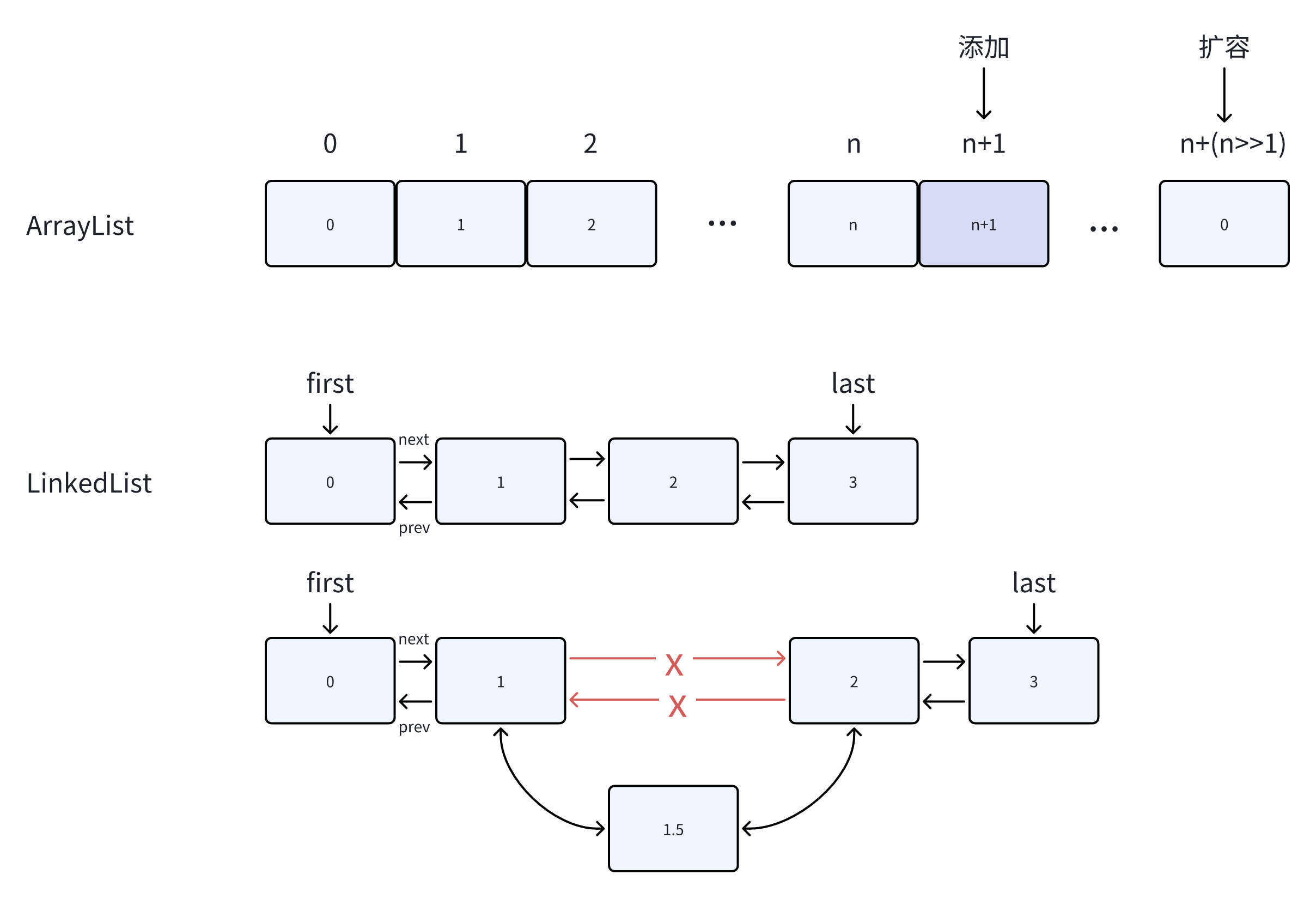
  • ArrayList是动态数组，因此会根据实际存储的元素个数进行动态地扩容，而对于Array类型被创建后就不能改变长度
  • ArrayList具备集合的各种常见操作，而Array只是一个固定长度的数组，不具备动态修改的能力

2.1.2. 泛型约束

  • ArrayList允许使用泛型确保类型安全，但也因此只能存储对象，Array可以存储对象也可以存储基本数据类型

2.1.3. 容量

  • ArrayList创建时不需要声明大小，Array创建时需要

2.2. ArrayList和LinkedList的区别

2.2.1. 随机访问性

  • ArrayList基于数组实现，具有随机访问性，可以通过get(int index)直接通过数组下标获取，时间复杂度O(1)
  • LinkedList基于链表实现，不具备随机访问性，查找的平均时间复杂度是O(n)

2.2.2. 插入和删除操作

  • ArrayList更适合于查找，对于删除操作会涉及到元素的移动，因此平均时间复杂度是O(n)
  • LinkedList，对于头尾插入和删除，时间复杂度是O(1)，对于链表中间的插入和删除是O(n)
  • 虽然ArrayList和LinkedList的增删的时间复杂度都是O(n)，是因为遍历导致的时间复杂度，而增删的效率上，LinkedList只需要改变应用，而ArrayList需要移动元素

2.2.3. 内存占用

  • ArrayList基于数组实现，占用的是一块连续的内存空间，但是由于扩容机制会存在冗余的空间
  • LinkedList基于链表实现，存储的内存空间不连续，每个元素需要额外的空间去保存前后元素的引用

2.2.4. 使用场景

  • ArrayList适用于随机访问频繁、并且查找多于添加的场景
  • LinkedList适用于不需要随机访问、插入和删除操作更多的场景，实现队列和栈来满足FIFO和LIFO
    ArrayList和LinkedList
ArrayList和LinkedList

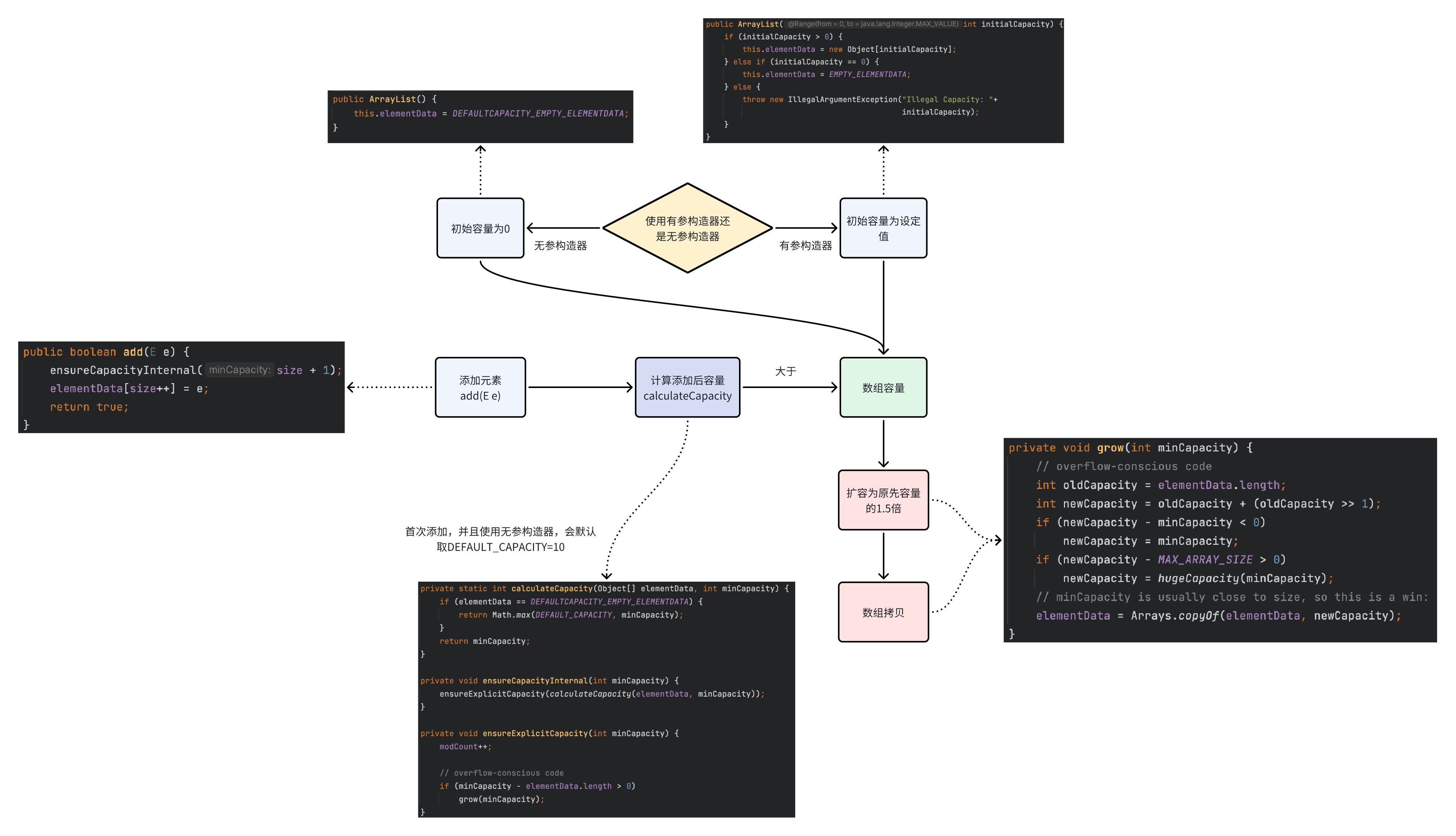
2.3. ArrayList扩容机制

2.3.1. 数组初始容量

  • 使用无参构造器，初始容量为0，而Vector较为特殊会设置初始容量为10
  • 使用有参构造器，初始容量为n

2.3.2. 添加后数组容量

  • 初次添加时，如果使用无参构造器，会默认取DEFAULT_CAPACITY=10作为添加后数组容量
  • 如果使用有参构造器，则计算数组容量为size+1

2.3.3. 比对容量

  • 数组计算容量大于数组容量，扩容为原先数组容量的1.5倍
  • 数组计算容量小于等于数组容量，不变

2.3.4. 时间复杂度

  • 如果只是末尾添加不扩容，时间复杂度O(1)
  • 如果需要扩容才能添加，则需要数组拷贝，因此时间复杂度O(n)
    ArrayList扩容机制
ArrayList扩容机制

2.4. ArrayList序列化

  • ArrayList使用transient修饰了elementData数组，意味着该属性无法被序列化
  • ArrayList内部实现了2个方法ReadObject和writeObject来自定义序列化策略
    • 之所以要自定义序列化策略，是为了提高序列化的效率，因为需要去掉扩容导致的冗余数组长度
// ArrayList使用transient修饰了elementData数组，意味着该属性无法被序列化
transient Object[] elementData; 
private void writeObject(java.io.ObjectOutputStream s)throws java.io.IOException{// Write out element count, and any hidden stuffint expectedModCount = modCount;s.defaultWriteObject();// Write out size as capacity for behavioural compatibility with clone()s.writeInt(size);// Write out all elements in the proper order.for (int i=0; i<size; i++) {s.writeObject(elementData[i]);}if (modCount != expectedModCount) {throw new ConcurrentModificationException();}
}
/*** Reconstitute the <tt>ArrayList</tt> instance from a stream (that is,* deserialize it).*/
private void readObject(java.io.ObjectInputStream s)throws java.io.IOException, ClassNotFoundException {elementData = EMPTY_ELEMENTDATA;// Read in size, and any hidden stuffs.defaultReadObject();// Read in capacitys.readInt(); // ignoredif (size > 0) {// be like clone(), allocate array based upon size not capacityint capacity = calculateCapacity(elementData, size);SharedSecrets.getJavaOISAccess().checkArray(s, Object[].class, capacity);ensureCapacityInternal(size);Object[] a = elementData;// Read in all elements in the proper order.for (int i=0; i<size; i++) {a[i] = s.readObject();}}
}

2.5. 如何实现ArrayList线程安全

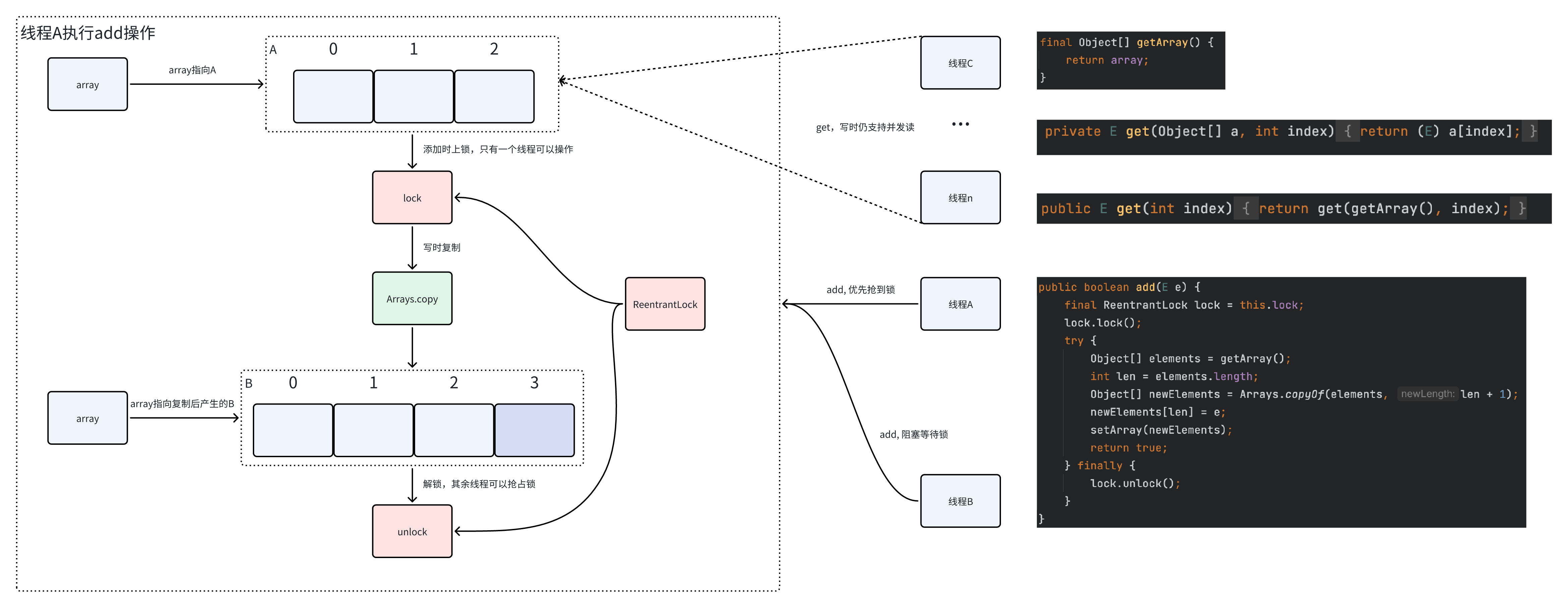
  • 使用Vector，不推荐，所有的方法都使用了synchronized关键字，效率较低
  • 使用Collections.synchronizedList(new ArrayList())包装
  • 使用CopyOnWriteArrayList，线程安全版的ArrayList

2.6. CopyOnWriteArrayList

2.6.1. 设计思想

  • 采用CopyOnWrite，即写时复制，底层采用ReentrantLock上锁保证同步和数组拷贝实现
  • 采用读写分离策略，写写互斥，读写不互斥，读读不互斥
  • 由于采用复制数值的形式修改，因此更适用于读多写少的情景

2.6.2. 具体操作细节

  • 读操作时不加锁，因此其他线程写操作时仍可以执行并发读，时间复杂度O(1)
  • 写操作时上锁，添加元素需要采用数组拷贝的方式，拷贝完使原引用指向新引用，因此时间复杂度是O(n)

2.6.3. 可能出现的问题

  • 数据不一致性，如果线程1通过getArray()方法先获取了array引用A，线程2利用修改方法修改了array引用为B，然后线程1还是会从array引用A中读取数据
  • 写操作开销大，需要数组拷贝，需要时间，也需要额外的内存空间
    CopyOnWriteArrayList的读写操作过程
CopyOnWriteArrayList的读写操作过程

3. Map

3.1. HashMap和HashTable区别

3.1.1. 线程安全性

  • HashMap是线程不安全的，HashTable是线程安全的
  • HashTable内部都是通过synchronized修饰的，效率低下，更推荐使用ConcurrentHashMap
  • HashMap多线程环境下问题
    • 死循环问题
      • JDK1.7之前，HashMap在多线程环境下扩容操作可能存在死循环问题，多个线程同时对链表进行操作，由于头插法可能会导致链表中的节点指向错误位置，从而形成环形链表导致死循环问题
      • JDK1.8之后，HashMap采用尾插法改进后，保证插入的节点永远是放在链表末尾，从而避免了产生环形结构，但是多线程环境下还是推荐使用ConcurrentHashMap
    • put导致元素丢失
      • 多线程操作时，线程A放入的键值可能会被线程B放入的键值覆盖
    • put和get并发时，导致get获取为null
      • 多线程操作时，线程A执行put并且还在扩容填充元素，而线程B此时执行get，就会出现此问题

3.1.2. 运行效率

  • HashMap比HashTable效率更高，因为HashTable方法基于synchronized修饰
  • 如果没有发生哈希冲突，HashMap的查找效率是O(1)

3.1.3. 底层数据结构

  • HashTable采用数组+链表，不支持NULL键和NULL值
  • HashMap采用数组+链表+红黑树，红黑树用于解决链表过长问题，支持NULL键和NULL值

3.1.4. 哈希函数实现

  • HashTable直接使用key的hashCode值
  • HashMap将key的hashCode值进行了高位和低位的混合处理提高分布均匀性，从而减少碰撞
  • 哈希函数有哪些构造方法
    • 直接定址法，h(key) = key
    • 除留余数法，h(key) = key % n，最常用
    • 数字分析法，h(key) = key中某些位置(如十位和百味)
    • 平方取中法，h(key) = key^2的中间几位
    • 折叠法，h(key) = key_1 + key_2 + … key_i (分割成位数相同的i段，然后求叠加和)
  • 解决哈希冲突的方法
    • 再哈希法，使用多个哈希函数，某个哈希函数冲突，就换用下一个，直至找到空位置
    • 开放地址法
      • 线性探测法，h(key) = p + i 从冲突位置p开始，逐个往后找到空位置，
      • 二次探测，h(key) = p + (-1)^(i+1) * d^2 ，从冲突位置p开始，以右左循环的方式探测，i代表探测次数，d代表距离
    • 拉链法，发生哈希冲突时，使用链表将冲突的元素连接起来
static final int hash(Object key) {int h;return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

3.1.5. 扩容机制

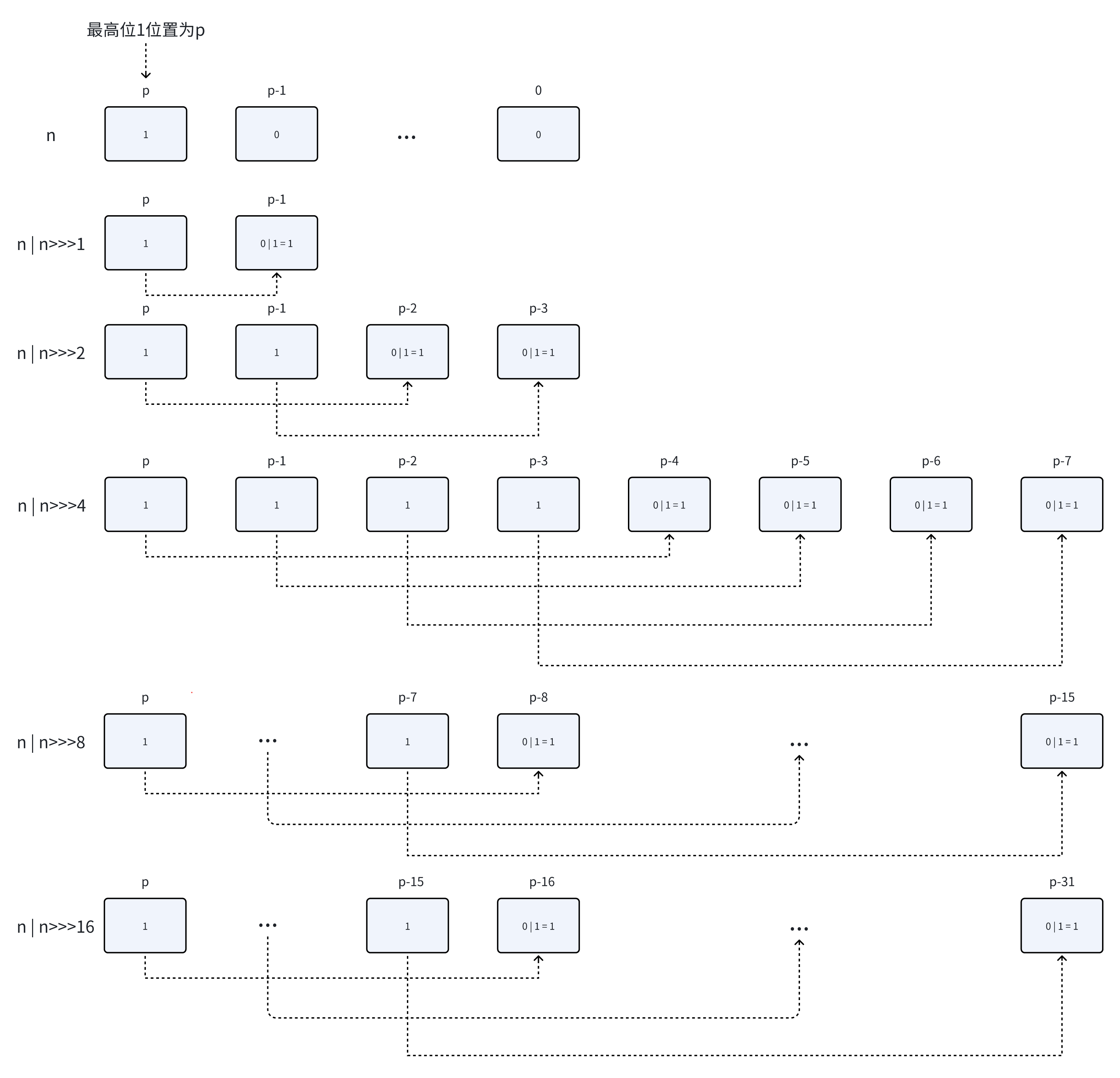
  • 未设置初始容量
    • HashTable默认大小为11，之后每次扩容为原先的2n+1
    • HashMap默认大小为0，首次扩容长度为16，之后每次扩容为原先的2n
  • 设置了初始容量
    • HashTable会直接使用给定的大小
    • HashMap会将其扩容至2的幂次方大小，如设置初始容量17，就会直接初始化为32
      • 原理就是将最高位的1传播，传播范围从1->2->4->8->16->32
  • 扩容机制
    • 扩容长度是2的幂次方
      • 可以更好的保证数组元素分配的更加均匀
      • 更方便使用位运算操作&，来替代取余操作%，运算效率会更高
    • 扩容时，旧的索引位置j会根据newCap重新调整为新的索引位置p，详细可看HashMap简单实现
      • 由于newCap是oldCap的2倍，那么对于newCap-1和oldCap-1，newCap低位会多一位掩码1，设为第k位【比如oldCap-1为0…01111，那么newCap-1就为0…11111】
      • newCap = oldCap + 2^k
      • oldCap = 2^k
      • 由于只是多了1位掩码，低位的运算都不会变，只需要考虑第k位，那么当hashcode & (newCap-1)
        • 假如hashcode二进制第k位是1，那么链表索引位置就会调整到p = j+2^k = j + oldCap
        • 假如hashcode二进制第k位是0，那么原先链表的索引位置就不变，p = j
/*** Returns a power of two size for the given target capacity.*/
static final int tableSizeFor(int cap) {int n = cap - 1;n |= n >>> 1;n |= n >>> 2;n |= n >>> 4;n |= n >>> 8;n |= n >>> 16;return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}

如何扩容至最近的2的幂次方，传播过程示意图

如何扩容至最近的2的幂次方，传播过程示意图

3.2. HashMap的基础参数

  • loadFactor，负载因子，掌控HashMap数据分布的疏密程度
    • loadFactor默认因子是0.75，即当总节点个数超过容量的75%，就会扩容
    • loadFactor越大意味着越稠密，哈希冲突的概率就越高，查找元素的效率会比较低
    • loadFactor越小意味着越稀疏，数组的利用率就会越低，空间成本大
  • threshold，数组阈值，是数组是否扩容的标准
    • threshold=capacity * loadFactor，当所有元素个数size大于threshold，则扩容数组长度和阈值
  • TREEIFY_THRESHOLD，链表树化阈值，是链表是否转为红黑树的标准
    • 链表树化阈值是8，并且需要满足数组长度大于等于64
  • UNTREEIFY_THRESHOLD ，红黑树链化阈值，是红黑树转为链表的标准
    • 之所以设置为6而不是8，是因为树化的阈值刚好在8附近，如果节点不断增加，就会导致过度转化
public class HashMap<K,V> extends AbstractMap<K,V> implements Map<K,V>, Cloneable, Serializable {// 序列号private static final long serialVersionUID = 362498820763181265L;// 默认的初始容量是16static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;// 最大容量static final int MAXIMUM_CAPACITY = 1 << 30;// 默认的负载因子static final float DEFAULT_LOAD_FACTOR = 0.75f;// 当链表上的结点数大于这个值时会转成红黑树static final int TREEIFY_THRESHOLD = 8;// 当树上的结点数小于等于这个值时树转链表static final int UNTREEIFY_THRESHOLD = 6;// 链表结构转化为红黑树对应的数组的最小长度static final int MIN_TREEIFY_CAPACITY = 64;// 存储元素的数组，总是2的幂次倍transient Node<k,v>[] table;// 一个包含了映射中所有键值对的集合视图transient Set<map.entry<k,v>> entrySet;// 所有存放元素的个数，注意这个不等于数组的长度transient int size;// 每次扩容和更改map结构的计数器transient int modCount;// 阈值(容量*负载因子) 当实际大小超过阈值时，会进行扩容int threshold;// 负载因子final float loadFactor;
}

3.3. HashMap的put流程

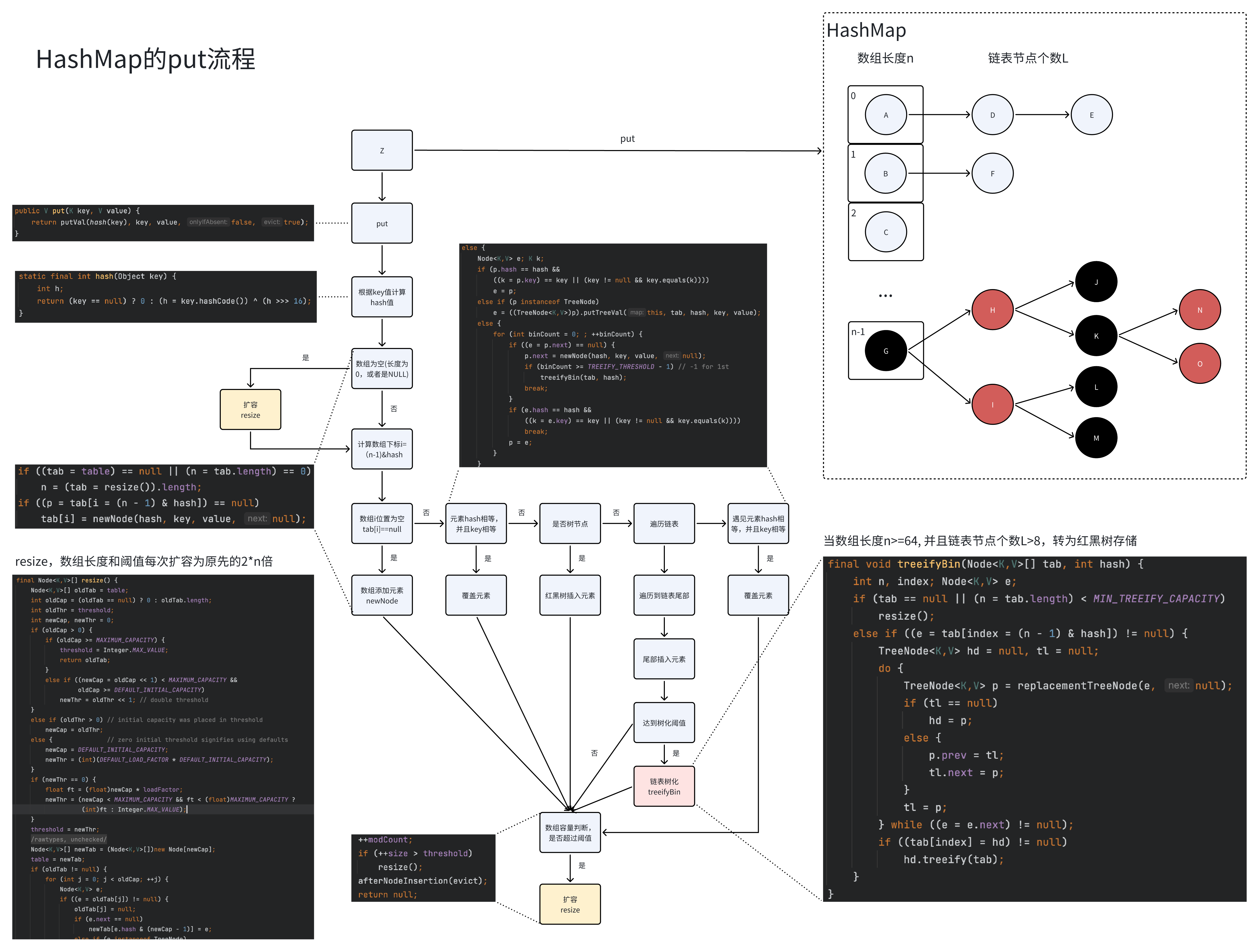
  • 通过hash方法计算key的哈希值
    • 先获取key的hashcode，然后将hashcode的低16位与高16位做异或操作【扰动】
    • 由于数组长度n是2的幂次，n-1就等于【2^k-1】，可以看成k位全1的地位掩码，那么当【n-1&hash】实际上就只利用了低k位，高32-k位就浪费了，因此为了利用这些高位，可以将hashcode右移16位，这样低16位和高16位就处在了同样的位置，此时再做异或，就成功融合了高位和低位的信息，进而减少了哈希冲突
  • 根据(n-1&hash)计算元素所在数组下标
  • 比较容器元素
    • 如果是链表，遍历容器中的元素，如果某个元素hash值相等并且key值相等，直接覆盖，否则插入尾部
      • 如果插入后，链表节点个数超过8，并且数组长度大于等于64，需要把链表转为红黑树
      • 如果链表节点小于等于6，那么会把红黑树转为链表
    • 如果是红黑树，直接插入
    • 最后插入后，还需要比较哈希表中总节点个数size是否超过阈值threshold，超过则扩容
      HashMap的put过程
HashMap的put过程

3.4. HashMap的简单实现

import java.util.Arrays;
public class SimpleHashMap<K, V> {private int INITIAL_LENGTH = 16;private double LOAD_FACTOR = 0.75f;private int threshold;class Node<K, V> {int hash;K key;V val;Node<K, V> next;Node(int hash, K key, V val) {this.hash = hash;this.key = key;this.val = val;this.next = null;}}private Node<K, V>[] tables;private int size;public SimpleHashMap() {this.tables = new Node[INITIAL_LENGTH];this.threshold = (int) (tables.length * LOAD_FACTOR);}public SimpleHashMap(int cap) {this.tables = new Node[getBinaryIndex(cap)];this.threshold = (int) (tables.length * LOAD_FACTOR);}public Node<K, V>[] getTables() {return this.tables;}public Integer getTableLength() {return this.tables.length;}private int getSize() {return this.size;}public int getBinaryIndex(int x) {x -= 1;x |= x >>> 1;x |= x >>> 2;x |= x >>> 4;x |= x >>> 8;x |= x >>> 16;return x + 1;}private int hash(K key) {if (key == null) {return 0;}int h = key.hashCode();return h ^ (h >>> 16);}private Node<K, V> newNode(int hash, K key, V val) {return new Node<>(hash, key, val);}// 简单版resize，需要额外创建节点private void resize() {int oldCap = tables.length;int newCap = oldCap << 1;Node<K, V>[] newTabs = new Node[newCap];// 链表重哈希for (int i = 0; i < oldCap; i++) {Node<K, V> e = tables[i];while (e != null) {int j = e.hash & (newCap - 1);if (newTabs[j] == null) {newTabs[j] = newNode(e.hash, e.key, e.val);} else {Node<K, V> p = newTabs[j];while (p.next != null) {p = p.next;}p.next = newNode(e.hash, e.key, e.val);}e = e.next;}}tables = newTabs;threshold <<= 1;}// HashMap底层写法版resize，不需要额外创建节点，而是通过指针的方式将原先链表重新串成2条链，节省空间private void resizePlus() {int oldCap = tables.length;int newCap = oldCap << 1;Node<K, V>[] newTabs = new Node[newCap];// 链表重哈希for (int j = 0; j < oldCap; j++) {Node<K, V> e = tables[j];if (e == null) {continue;}// 只有一个节点if (e.next == null) {newTabs[e.hash & (newCap - 1)] = e;continue;}// 低位链头尾指针Node<K,V> loHead = null, loTail = null;// 高位链头尾指针Node<K,V> hiHead = null, hiTail = null;do {// 低位链串起来if ((e.hash & oldCap) == 0) {if (loHead == null) {loHead = e;} else {loTail.next = e;}loTail = e;// 高位链串起来} else {if (hiHead == null) {hiHead = e;} else {hiTail.next = e;}hiTail = e;}e = e.next;} while (e != null);// 低位链, 即第k位为0, 因此最终映射位置仍为jif (loTail != null) {loTail.next = null;newTabs[j] = loHead;}// 高位链, 即第k位为1, 因此最终映射位置为j + oldCapif (hiTail != null) {hiTail.next = null;newTabs[j + oldCap] = hiHead;}}tables = newTabs;threshold <<= 1;}private void put(K key, V val) {putVal(hash(key), key, val);}private void putVal(int hash, K key, V val) {int n = tables.length;int i = hash & (n - 1);if (tables[i] == null) {tables[i] = newNode(hash, key, val);++size;return;}Node<K, V> e = tables[i];while (e.next != null) {if (e.hash == hash && (e.key == key || e.key.equals(key))) {e.val = val;return;}e = e.next;}e.next = newNode(hash, key, val);// 大于阈值扩容if (++size > threshold) {resizePlus();}}private V get(K key) {return getVal(hash(key), key);}private V getVal(int hash, K key) {int n = tables.length;int i = hash & (n - 1);Node<K, V> e = tables[i];while (e != null) {if (e.hash == hash && (e.key == key || e.key.equals(key))) {return e.val;}e = e.next;}return null;}public static void main(String[] args) {SimpleHashMap<String, Integer> map = new SimpleHashMap<>(10);for (int i = 1000000; i <= 1000100; i++) {map.put(String.valueOf(i), i);System.out.println(i + ":" + map.getTableLength());SimpleHashMap<String, Integer>.Node<String, Integer>[] tables = map.getTables();int j = 0;for (SimpleHashMap<String, Integer>.Node<String, Integer> table : tables) {if (table != null) {System.out.printf("table[%d]=[%s:%d]", j++, table.key, table.val);SimpleHashMap<String, Integer>.Node<String, Integer> e = table;while (e.next != null) {e = e.next;System.out.printf("->[%s:%d]", e.key, e.val);}} else {System.out.printf("table[%d]=null", j++);}System.out.println();}}}
}
/*
达到24阈值时，扩容机制举例，链表节点迁移
1000023:32
table[0]=[1000003:1000003]->[1000014:1000014]
table[1]=[1000004:1000004]->[1000015:1000015]
table[2]=[1000005:1000005]->[1000016:1000016]
table[3]=[1000006:1000006]->[1000017:1000017]
table[4]=[1000010:1000010]->[1000021:1000021]
table[5]=[1000000:1000000]->[1000011:1000011]->[1000022:1000022]
table[6]=[1000001:1000001]->[1000012:1000012]->[1000023:1000023]
table[7]=[1000002:1000002]->[1000013:1000013]
table[8]=null
table[9]=null
table[10]=null
table[11]=null
table[12]=[1000007:1000007]->[1000018:1000018]
table[13]=[1000008:1000008]->[1000019:1000019]
table[14]=[1000009:1000009]
table[15]=null
table[16]=null
table[17]=null
table[18]=null
table[19]=null
table[20]=null
table[21]=null
table[22]=null
table[23]=null
table[24]=null
table[25]=null
table[26]=null
table[27]=[1000020:1000020]
table[28]=null
table[29]=null
table[30]=null
table[31]=null
1000024:64
table[0]=[1000003:1000003]
table[1]=[1000004:1000004]
table[2]=[1000005:1000005]
table[3]=[1000006:1000006]
table[4]=[1000021:1000021]
table[5]=[1000000:1000000]->[1000022:1000022]
table[6]=[1000001:1000001]->[1000023:1000023]
table[7]=[1000002:1000002]->[1000024:1000024]
table[8]=null
table[9]=null
table[10]=null
table[11]=null
table[12]=[1000007:1000007]
table[13]=[1000008:1000008]
table[14]=[1000009:1000009]
table[15]=null
table[16]=null
table[17]=null
table[18]=null
table[19]=null
table[20]=null
table[21]=null
table[22]=null
table[23]=null
table[24]=null
table[25]=null
table[26]=null
table[27]=[1000020:1000020]
table[28]=null
table[29]=null
table[30]=null
table[31]=null
table[32]=[1000014:1000014]
table[33]=[1000015:1000015]
table[34]=[1000016:1000016]
table[35]=[1000017:1000017]
table[36]=[1000010:1000010]
table[37]=[1000011:1000011]
table[38]=[1000012:1000012]
table[39]=[1000013:1000013]
table[40]=null
table[41]=null
table[42]=null
table[43]=null
table[44]=[1000018:1000018]
table[45]=[1000019:1000019]
table[46]=null
table[47]=null
table[48]=null
table[49]=null
table[50]=null
table[51]=null
table[52]=null
table[53]=null
table[54]=null
table[55]=null
table[56]=null
table[57]=null
table[58]=null
table[59]=null
table[60]=null
table[61]=null
table[62]=null
table[63]=null*/

3.5. LinkedHashMap

3.5.1. LinkedHashMap特点

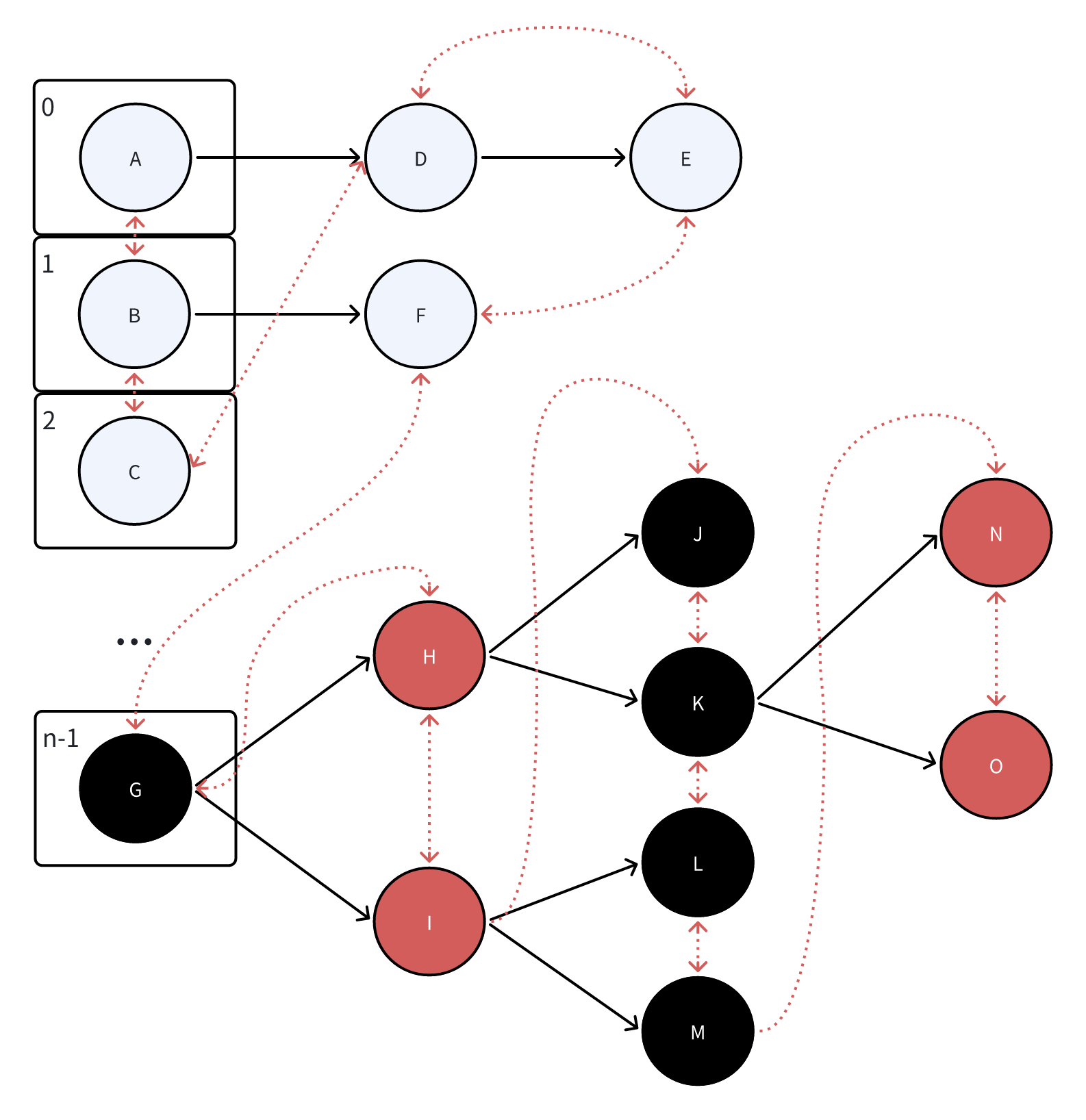
  • LinkedHashMap继承了HashMap
    • 并对每个entry使用指针额外维护了先后关系【before，after】
    • 因此可以按照插入的顺序进行遍历
      HashMap的Entry属性LinkedHashMap使用双向链表维护了节点的先后关系
HashMap的Entry属性

3.5.2. LinkedHashMap实现LRU

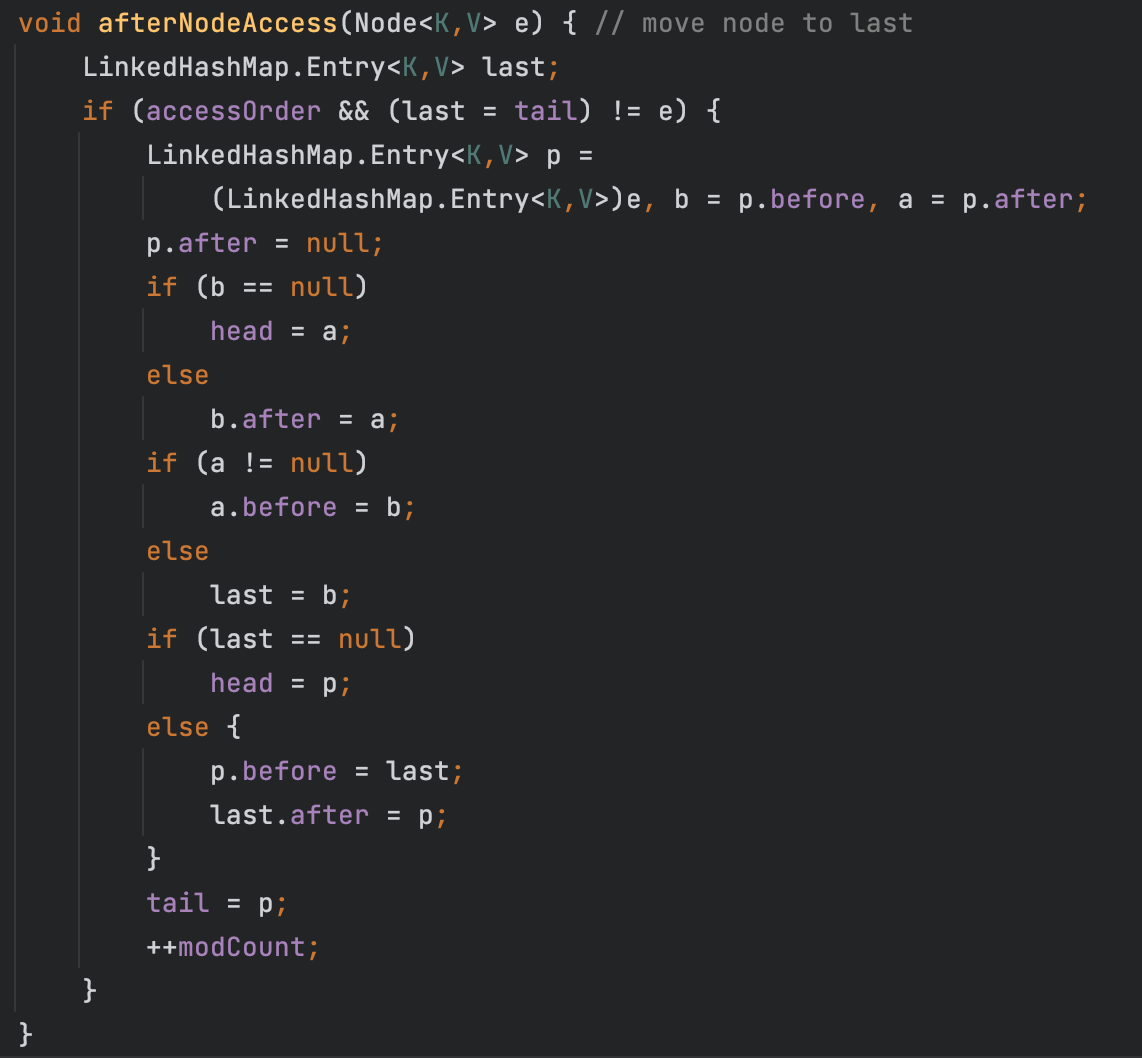
  • LinkedHashMap继承了HashMap，并在原先entry的基础上额外添加了before和after两个指针，用于记录元素的插入顺序，因此LinkedHashMap能够按照插入顺序或访问顺序迭代元素，而HashMap迭代元素的顺序是不确定的
  • 当accessOrder=true时，每次访问一个节点时，会将该节点移动到链表末尾
  • 可以通过将accessOrder设置为true，并重写removeEldestEntry方法，来实现LRU缓存
    设置accessOrder=true，会将节点移动到最后
设置accessOrder=true，会将节点移动到最后 
public class Main {// 通过继承LinkedHashMap并重写removeEldestEntry来实现LRUstatic class LRUCache<K,V> extends LinkedHashMap<K,V> {public final int cap;public LRUCache(int cap) {// 第三个参数accessOrder需要设置为true，这样访问元素时会将其移动至链表尾部super(cap, 0.75f, true);this.cap = cap;}// 当节点数量多于容量，会移除链表头结点@Overrideprotected boolean removeEldestEntry(Map.Entry<K,V> eldest) {return size() > cap;}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);// 输入数量int n = scanner.nextInt();// LRU的容量大小int m = scanner.nextInt();LRUCache<Integer, Integer> LRUCache = new LRUCache<>(m);int cnt = 0;for (int i=1;i<=n;i++) {int x = scanner.nextInt();LRUCache.put(x, ++cnt);List<Integer> list = new ArrayList<>(LRUCache.keySet());Collections.reverse(list);System.out.println(list);}}
}

import java.util.*;
// 通过添加和移除逻辑来实现LRU
public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);LinkedHashMap<Integer, Integer> linkedHashMap = new LinkedHashMap<>();// 输入数量int n = scanner.nextInt();// LRU的容量大小int m = scanner.nextInt();int cnt = 0;for (int i=1;i<=n;i++) {int x = scanner.nextInt();if (linkedHashMap.size() < m) {} else if (linkedHashMap.containsKey(x)) {linkedHashMap.remove(x);} else {linkedHashMap.remove(linkedHashMap.entrySet().iterator().next().getKey());}linkedHashMap.put(x, ++cnt);List<Integer> list = new ArrayList<>(linkedHashMap.keySet());Collections.reverse(list);System.out.println(list);}}
}

3.6. TreeMap

3.6.1. TreeMap特点

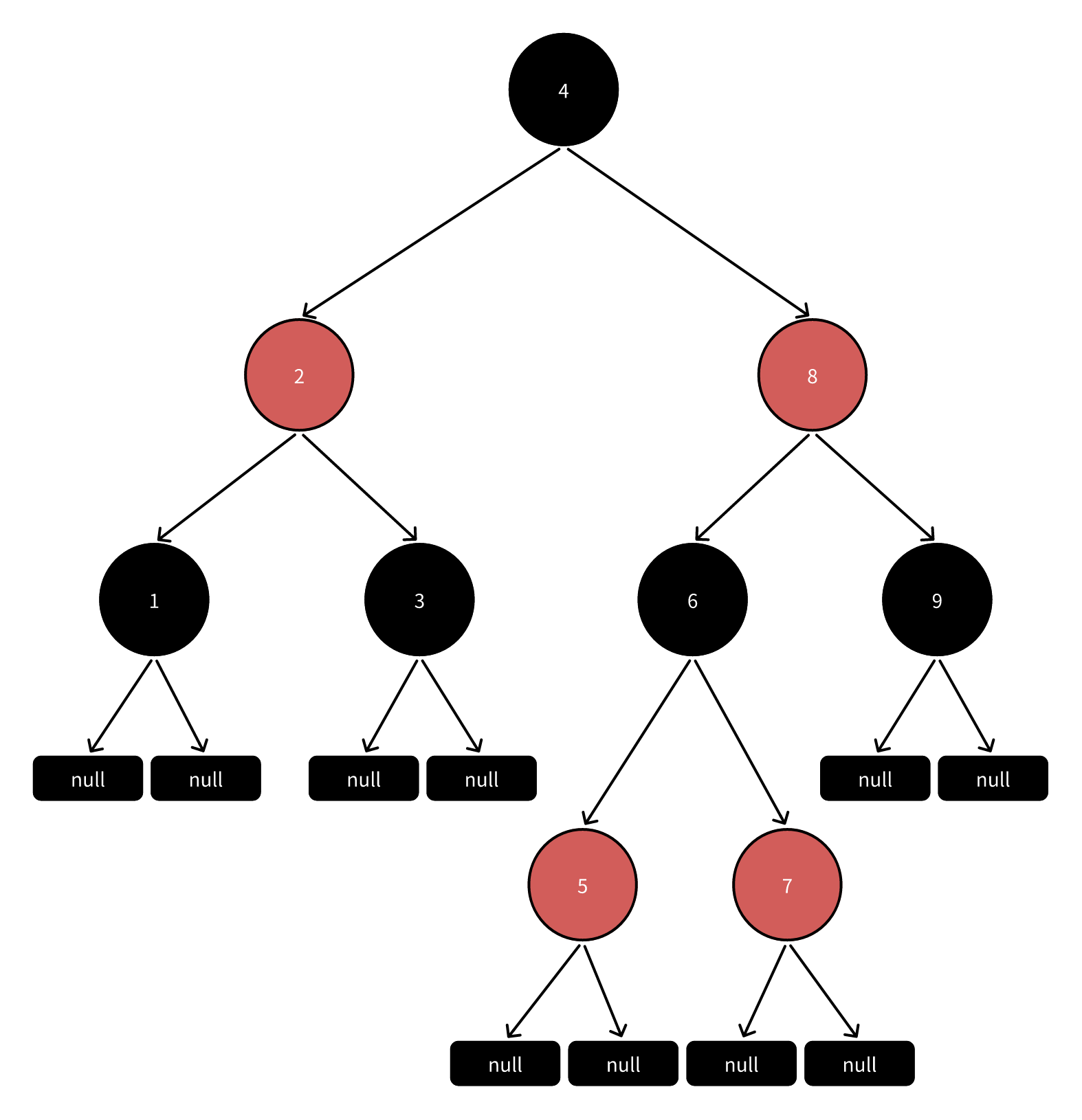
  • TreeMap底层是红黑树，是一种自平衡的二叉查找树
    • 平衡因子不会大于1（每个节点的左右子树高度最多相差1）
    • 需要通过旋转的方式保持树的平衡
    • 查找、插入、删除平均时间复杂度均是O(logn)
    • 二叉查找树，每个节点都大于左子树的任何一个节点，小于右子树的任何一个节点，节点具有顺序性
  • TreeMap通过key的比较器决定元素的顺序，可以传入比较器Comparator
    红黑树，自平衡的二叉查找树
红黑树，自平衡的二叉查找树

3.6.2. 红黑树特点

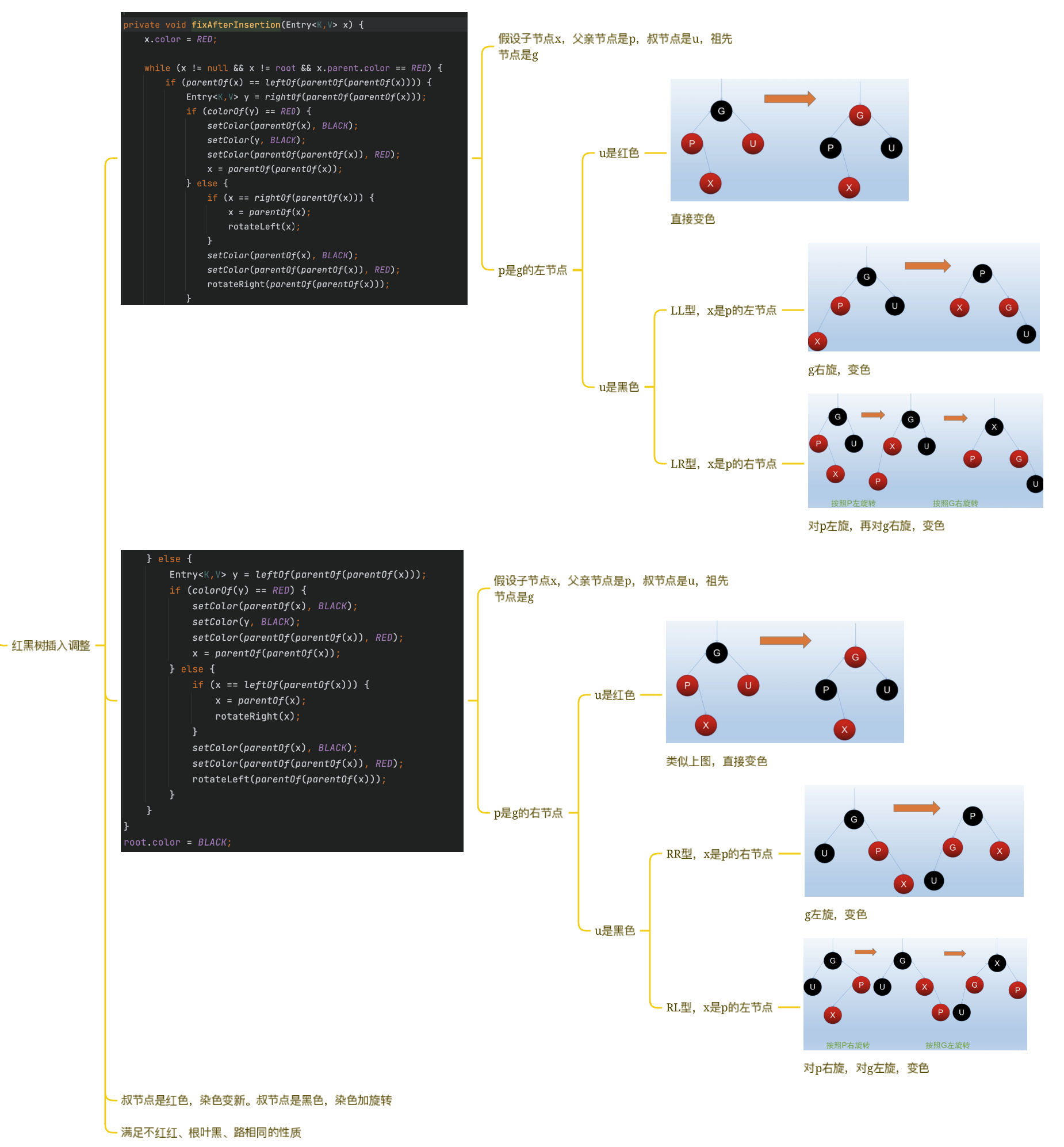
  • 根节点和叶子节点都是黑色
  • 每个节点要么是红色，要么是黑色
  • 红色节点的父节点和子节点必然是黑色的
  • 从任意节点到其叶子节点的路径都包含相同数量的黑色节点
  • 408口诀，根叶黑，不红红，路相同

3.6.3. 红黑树插入调整

3.7. ConcurrentHashMap

3.7.1. ConcurrentHashMap特点

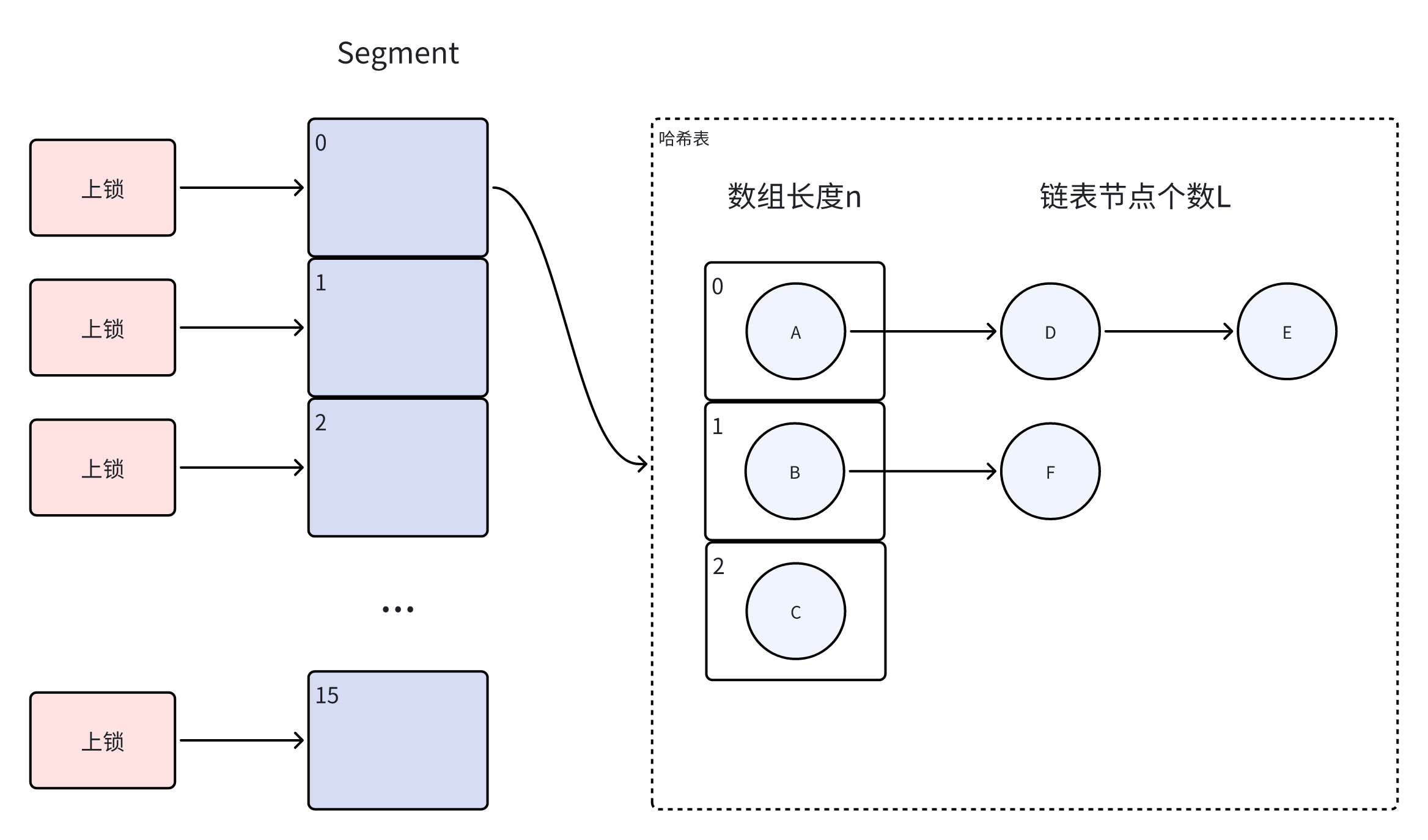
  • JDK1.7
    • ConcurrentHashMap由Segment数组和哈希表组成，每个Segment对应一个可扩容哈希表
    • ConcurrentHashMap通过对Segment数组进行上锁从而实现同步
    • ConcurrentHashMap的Segment数组长度n一旦初始化就不可改变，默认是16，代表了可支持最大的线程并发数，每个Segment上同一时间只能有一个线程可以操作
      JDK1.7，ConcurrentHashMap对Segment上锁
JDK1.7，ConcurrentHashMap对Segment上锁
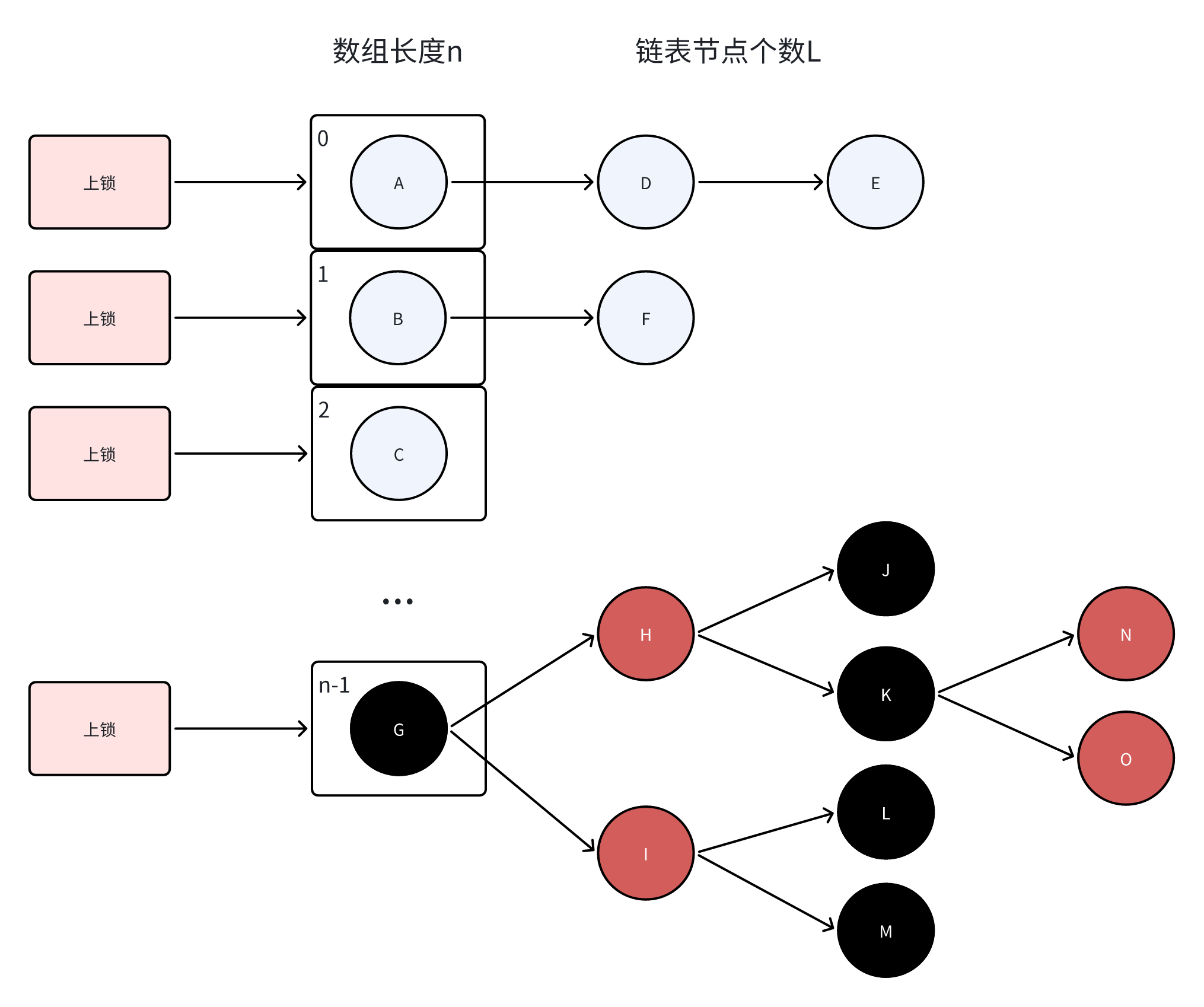
  • JDK1.8及以后
    • ConcurrentHashMap通过自旋、CAS、synchronized操作HashMap实现同步
    • ConcurrentHashMap通过对Node数组使用synchronized上锁从而实现同步
      JDK1.8，Concurrent取消了Segment结构，改为数组、链表和红黑树，对数组上锁
JDK1.8，Concurrent取消了Segment结构，改为数组、链表和红黑树，对数组上锁

3.7.2. ConcurrentHashMap源码分析

3.7.2.1. initTable，初始化Node数组
  • 变量sizeCtl，用于判断table的状态
    • -1，表明table正在初始化，其他线程需要自旋，让出CPU
    • 0，表明table初始大小，表明没有被初始化
    • n，表示table扩容的阈值，表明table已经初始化
private final Node<K,V>[] initTable() {Node<K,V>[] tab; int sc;// 线程自旋while ((tab = table) == null || tab.length == 0) {// 如果有线程CAS执行成功，正在初始化tab, 需要执行yield让出CPUif ((sc = sizeCtl) < 0)Thread.yield(); // 从内存中取出SIZECTL，判断值是不是sc，如果是修改为-1else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) {try {if ((tab = table) == null || tab.length == 0) {int n = (sc > 0) ? sc : DEFAULT_CAPACITY;@SuppressWarnings("unchecked")Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n];table = tab = nt;// sc = (3/4)nsc = n - (n >>> 2);}} finally {sizeCtl = sc;}break;}}return tab;
}
3.7.2.2. putVal，插入数据
  • 如果插入的数据，key或者value为空，则会直接抛出空指针异常
  • 如果数组位置为空，使用CAS机制尝试写入，失败则继续自旋保证写入成功
  • 如果数组位置不为空，需要遍历链表，此时利用synchronized上锁写入数据
public V put(K key, V value) {return putVal(key, value, false);
}
final V putVal(K key, V value, boolean onlyIfAbsent) {// ConcurrentHashMap不允许key和value为空if (key == null || value == null) throw new NullPointerException();int hash = spread(key.hashCode());int binCount = 0;for (Node<K,V>[] tab = table;;) {Node<K,V> f; int n, i, fh;// 初始化Node数组if (tab == null || (n = tab.length) == 0)tab = initTable();// 对应位置为空，CAS尝试写入else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {if (casTabAt(tab, i, null,new Node<K,V>(hash, key, value, null)))break;                   // no lock when adding to empty bin}else if ((fh = f.hash) == MOVED)tab = helpTransfer(tab, f);else {V oldVal = null;// 对Node数组上锁synchronized (f) {if (tabAt(tab, i) == f) {if (fh >= 0) {binCount = 1;// 遍历链表插入for (Node<K,V> e = f;; ++binCount) {K ek;if (e.hash == hash &&((ek = e.key) == key ||(ek != null && key.equals(ek)))) {oldVal = e.val;if (!onlyIfAbsent)e.val = value;break;}Node<K,V> pred = e;if ((e = e.next) == null) {pred.next = new Node<K,V>(hash, key,value, null);break;}}}// 红黑树插入else if (f instanceof TreeBin) {Node<K,V> p;binCount = 2;if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,value)) != null) {oldVal = p.val;if (!onlyIfAbsent)p.val = value;}}}}if (binCount != 0) {if (binCount >= TREEIFY_THRESHOLD)treeifyBin(tab, i);if (oldVal != null)return oldVal;break;}}}addCount(1L, binCount);return null;
}
3.7.2.3. get，查找元素
  • ConcurrentHashMap读时无需获取锁，支持写时并发读
public V get(Object key) {Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek;int h = spread(key.hashCode());if ((tab = table) != null && (n = tab.length) > 0 &&(e = tabAt(tab, (n - 1) & h)) != null) {if ((eh = e.hash) == h) {if ((ek = e.key) == key || (ek != null && key.equals(ek)))return e.val;}else if (eh < 0)return (p = e.find(h, key)) != null ? p.val : null;while ((e = e.next) != null) {if (e.hash == h &&((ek = e.key) == key || (ek != null && key.equals(ek))))return e.val;}}return null;
}

4. Set

4.1. HashSet

4.1.1. HashSet特点

  • 本质是通过哈希映射h(key)判断元素是否存在
  • 底层使用HashMap实现
    • key用来存具体的值，value默认为PRESENT = new Object()
    • 判断是否存在，如果key的hashcode相等，并且key相等，就意味着这个值在hashMap中存在
public class HashSet<E>extends AbstractSet<E>implements Set<E>, Cloneable, java.io.Serializable {// 底层使用HashMap作为容器    private transient HashMap<E,Object> map;// value默认是objectprivate static final Object PRESENT = new Object();public HashSet() {map = new HashMap<>();}public HashSet(Collection<? extends E> c) {map = new HashMap<>(Math.max((int) (c.size()/.75f) + 1, 16));addAll(c);}public HashSet(int initialCapacity, float loadFactor) {map = new HashMap<>(initialCapacity, loadFactor);}public HashSet(int initialCapacity) {map = new HashMap<>(initialCapacity);}HashSet(int initialCapacity, float loadFactor, boolean dummy) {map = new LinkedHashMap<>(initialCapacity, loadFactor);}public boolean add(E e) {return map.put(e, PRESENT)==null;}public boolean contains(Object o) {return map.containsKey(o);}public boolean remove(Object o) {return map.remove(o)==PRESENT;}
}

4.2. TreeSet

4.2.1. TreeSet特点

  • 本质是利用红黑树对键值的排序规则
  • 底层使用TreeMap实现
    • key用来存具体的值，value默认为PRESENT = new Object()
    • 利用二叉查找树的性质，在TreeMap上查找具体的key值返回
public class TreeSet<E> extends AbstractSet<E>implements NavigableSet<E>, Cloneable, java.io.Serializable {private transient NavigableMap<E,Object> m;private static final Object PRESENT = new Object();TreeSet(NavigableMap<E,Object> m) {this.m = m;}public TreeSet() {this(new TreeMap<E,Object>());}public TreeSet(Comparator<? super E> comparator) {this(new TreeMap<>(comparator));}public TreeSet(Collection<? extends E> c) {this();addAll(c);}public TreeSet(SortedSet<E> s) {this(s.comparator());addAll(s);}public boolean add(E e) {return m.put(e, PRESENT)==null;}public boolean contains(Object o) {return m.containsKey(o);}public boolean remove(Object o) {return m.remove(o)==PRESENT;}
}

5. Queue

5.1. PriorityQueue

5.1.1. PriorityQueue特点

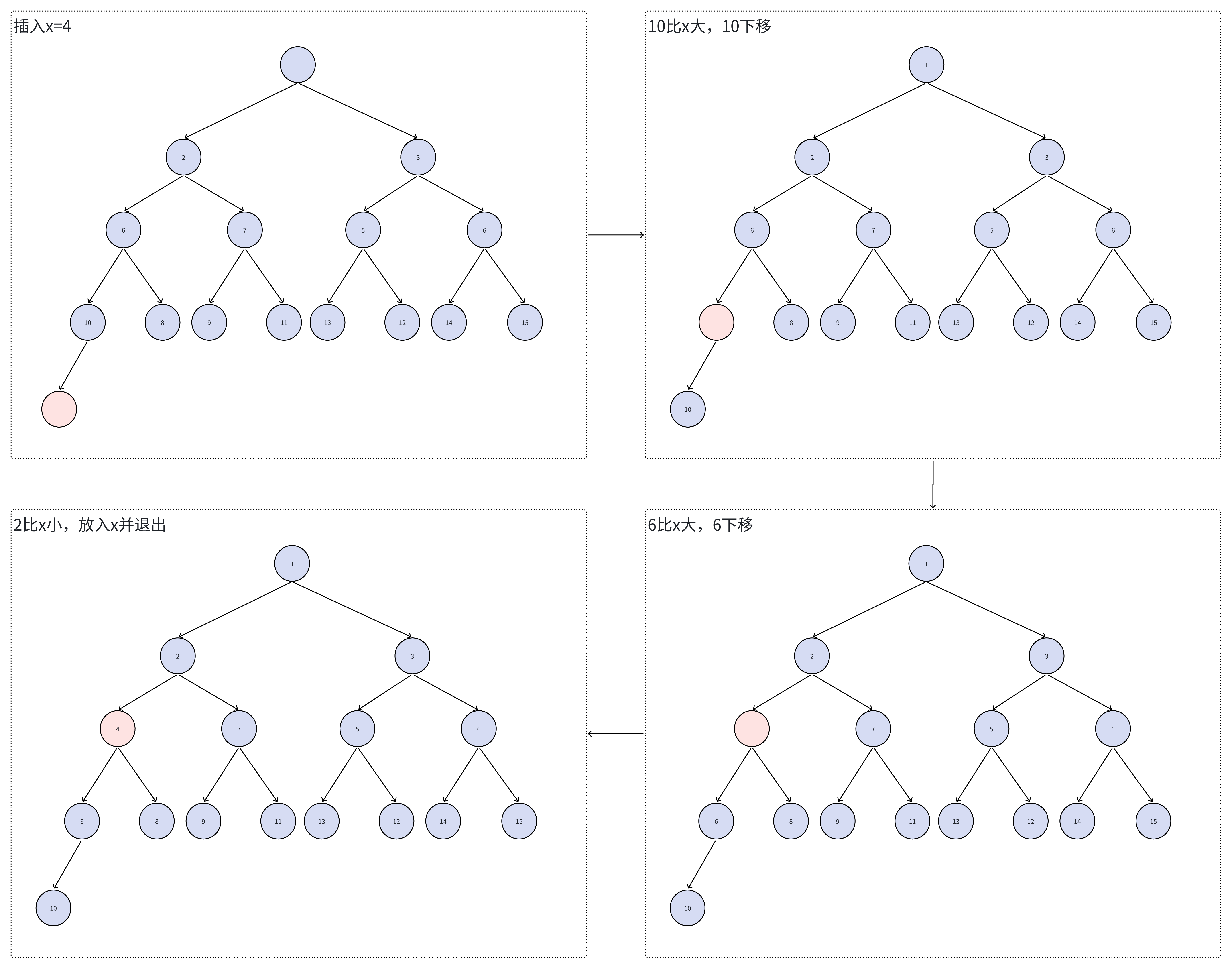
  • 优先队列，底层通过堆的方式实现，默认是小顶堆
  • 大顶堆，是一颗完全二叉树，任意节点均满足大于左子树和右子树的任一节点的性质
  • 小顶堆，是一颗完全二叉树，任意节点均满足小于左子树和右子树的任一节点的性质

5.1.2. PriorityQueue源码分析

5.1.2.1. siftUp，沿着链往上调整堆
  • 从堆节点k出发，k位置一开始是空的节点，希望往堆中插入值为x的元素
  • 沿着k所在的链往上逐个与父节点parent比较
  • 如果parent节点的值比x大就将parent元素下移，否则将x插入到当前位置并停止
private void siftUp(int k, E x) {if (comparator != null)siftUpUsingComparator(k, x);elsesiftUpComparable(k, x);
}
private void siftUpComparable(int k, E x) {Comparable<? super E> key = (Comparable<? super E>) x;while (k > 0) {int parent = (k - 1) >>> 1;Object e = queue[parent];if (key.compareTo((E) e) >= 0)break;queue[k] = e;k = parent;}queue[k] = key;
}
private void siftUpUsingComparator(int k, E x) {while (k > 0) {int parent = (k - 1) >>> 1;Object e = queue[parent];if (comparator.compare(x, (E) e) >= 0)break;queue[k] = e;k = parent;}queue[k] = x;
}

siftUp，算法过程

siftUp，算法过程
5.1.2.2. siftDown，向下调整堆
  • 从堆节点k出发，k位置一开始是空的节点，希望往堆中插入值为x的元素
  • 先比较k位置的2个子节点，选择更小的子节点child作为下一位置
  • 如果x值比child节点的值大，那么child节点上移并继续向下比较，否则将x插入当前位置并停止
private void siftDown(int k, E x) {if (comparator != null)siftDownUsingComparator(k, x);elsesiftDownComparable(k, x);
}
private void siftDownComparable(int k, E x) {Comparable<? super E> key = (Comparable<? super E>)x;int half = size >>> 1;        while (k < half) {int child = (k << 1) + 1; Object c = queue[child];int right = child + 1;if (right < size &&((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)c = queue[child = right];if (key.compareTo((E) c) <= 0)break;queue[k] = c;k = child;}queue[k] = key;
}
private void siftDownUsingComparator(int k, E x) {int half = size >>> 1;while (k < half) {int child = (k << 1) + 1;Object c = queue[child];int right = child + 1;if (right < size &&comparator.compare((E) c, (E) queue[right]) > 0)c = queue[child = right];if (comparator.compare(x, (E) c) <= 0)break;queue[k] = c;k = child;}queue[k] = x;
}

siftDown，算法过程

siftDown，算法过程
5.1.2.3. add，往堆中添加元素
  • 在堆的末尾额外添加一个位置i，堆大小加一，然后从位置i出发插入x，siftUp向上调整堆
public boolean add(E e) {return offer(e);
}
public boolean offer(E e) {if (e == null)throw new NullPointerException();modCount++;int i = size;if (i >= queue.length)grow(i + 1);size = i + 1;if (i == 0)queue[0] = e;elsesiftUp(i, e);return true;
}
5.1.2.4. poll，弹出堆顶
  • 将堆顶弹出，并将堆末尾拿出x，堆大小减一，然后从堆顶位置0出发插入x，siftDown向下调整堆
public E poll() {if (size == 0)return null;int s = --size;modCount++;E result = (E) queue[0];E x = (E) queue[s];queue[s] = null;if (s != 0)siftDown(0, x);return result;
}
5.1.2.5. remove，删除某元素
  • 有坑，删除固定元素需要遍历整个堆，平均时间复杂度是O(n)的，如果有这个使用场景，更推荐使用TreeSet
  • 删除某元素所在的位置k，并将堆末尾拿出x，堆大小减一，然后从位置k出发插入x，siftDown向下调整堆
    • 如果x插入的位置不在k，首先对于未删除时k所在堆顶的堆，肯定是符合堆性质的（也就是说这个堆中任何元素都会比k的父节点大），所以堆调整后，堆顶仍然是比k的父节点大的，符合整体堆性质
    • 如果x插入的位置在k，只能说明x是x所在堆顶的堆中最小的，那么还需要从k位置往上调整堆（因为无法判断x是否比k的父节点大）
public boolean remove(Object o) {// 会遍历整个堆int i = indexOf(o);if (i == -1)return false;else {removeAt(i);return true;}
}
private int indexOf(Object o) {if (o != null) {for (int i = 0; i < size; i++)if (o.equals(queue[i]))return i;}return -1;
}
private E removeAt(int i) {modCount++;int s = --size;if (s == i) queue[i] = null;else {E moved = (E) queue[s];queue[s] = null;siftDown(i, moved);if (queue[i] == moved) {siftUp(i, moved);if (queue[i] != moved)return moved;}}return null;
}

5.1.3. 找出List中前M个最大的数字

import java.util.*;
public class Main {public static void main(String[] args) {int n = 10000000;int m = 10;List<Integer> list = new ArrayList<>();for (int i=1;i<=n;i++) {list.add(i);}// 打乱Collections.shuffle(list);PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();for (Integer x : list) {if (priorityQueue.size() < m) {priorityQueue.add(x);continue;}// 如果元素x比堆中最小的元素大if (x > priorityQueue.peek()) {// 弹出堆顶，并放入元素xpriorityQueue.poll();priorityQueue.add(x);}}// list前m大priorityQueue.forEach(System.out::println);}
}

版权声明:

本网仅为发布的内容提供存储空间，不对发表、转载的内容提供任何形式的保证。凡本网注明“来源：XXX网络”的作品，均转载自其它媒体，著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处。

我们尊重并感谢每一位作者，均已注明文章来源和作者。如因作品内容、版权或其它问题，请及时与我们联系，联系邮箱：809451989@qq.com，投稿邮箱：809451989@qq.com

相关资讯

热文排行

最新新闻

推荐新闻

热搜词