6.11.各顶点间的最短路径问题-Floyd算法

一.前言：

对于Floyd算法，采用了动态规划的思想，核心内容是把一个大问题拆分为多个小问题再进行求解，每一个小问题之间有一个递进的关系，比如本篇中的Floyd算法，若求每一对顶点之间的最短路径，首先会把该问题分为n个阶段求解，求解的是对于任意一对顶点即Vi->Vj之间的最短路径，

首先设置一个初始阶段：该阶段不允许Vi->Vj之间的路径存在其他的中转顶点；

第二个阶段：会考虑如果允许v0顶点作为Vi->Vj之间的中转顶点，那么Vi->Vj之间的最短路径会不会有进一步的优化；

第三个阶段：会继续多考虑一个v1顶点，此时就成为如果允许v0、v1顶点作为中转顶点，那么Vi->Vj之间的最短路径会不会有更进一步的优化；

以此类推，这个问题会进行n轮的求解，因为总共有n个顶点，如下图：

二.Floyd算法：

1.实例：

如上图，以上述图片的有向图为例，现在求图中各个顶点对之间的最短路径，

开始-1号阶段（初始化阶段），如下图：

如上图，需要初始化两个矩阵即两个二维数组，第一个矩阵是A矩阵，第二个矩阵是path矩阵，

第一个矩阵即A矩阵就是该图的邻接矩阵，矩阵A表示就目前来看，能找到的各个顶点对之间的最短路径长度是多少，初始阶段是不允许各个顶点对之间的路径存在中转顶点，所以就目前来看，比如v0到v2的最短路径长度就是13，因为现在这个阶段是不允许以v1顶点作为中转顶点加入的，因此v0行v2列的值为13；

第二个矩阵path指的是目前能够找到的顶点对之间最短路径中的中转顶点，刚开始所有顶点对之间都不可以有中转顶点，所以初始化时会把所有的path值都设为-1（之所以设为-1，是因为-1不是图中任何一个顶点的索引，-1可以表示不存在）。

如下图：

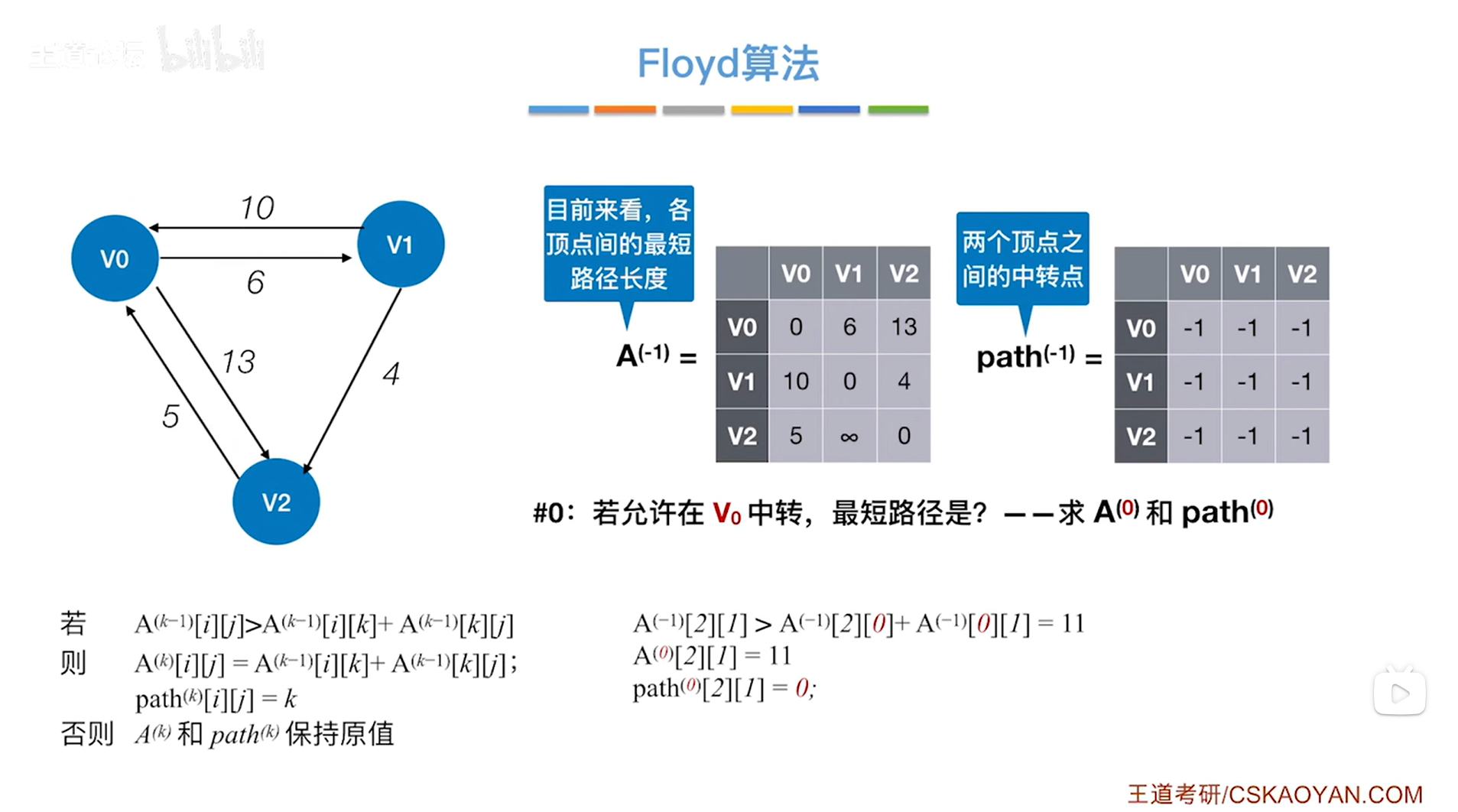
如上图，左下角的公式就是求从k-1阶段（前一阶段）到k阶段（当前阶段）中A矩阵和path矩阵的公式，该公式解读如下：

k代表当前阶段，也代表当前中转顶点的编号；k-1代表前一个阶段
A(k-1)[i] [j]表示前一个阶段的A矩阵中顶点i到顶点j的最短路径长度
A(k-1)[i] [k]表示前一个阶段的A矩阵中顶点i到顶点k的路径长度
A(k-1)[k] [j]表示前一个阶段的A矩阵中顶点k到顶点j的路径长度
A(k-1)[i] [k]+A(k-1)[k] [j]就表示前一个阶段的A矩阵中顶点i到中转顶点k再到顶点j的路径长度
A(k)[i] [j]=A(k-1)[i] [k]+A(k-1)[k] [j]表示把前一个阶段的A矩阵中顶点i到中转顶点k再到顶点j的路径长度赋值给当前阶段的A矩阵中顶点i到顶点j的最短路径长度
path(k)[i] [j]=k就表示当前阶段中从顶点i到顶点j的路径中中转顶点为顶点k
因此上图左下角的公式A(k-1)[i] [j]>A(k-1)[i] [k]+A(k-1)[k] [j]就表示如果前一个阶段的A矩阵中顶点i到顶点j的最短路径长度大于前一个阶段的A矩阵中顶点i到中转顶点k再到顶点j的路径长度，那么就执行A(k)[i] [j]=A(k-1)[i] [k]+A(k-1)[k] [j]，且修改path的值为path(k)[i] [j]=k
A(k)和path(k)保持原值就是对应顶点A(k)等于A(k-1)，path(k)等于path(k-1)
总而言之，就是如果前一阶段中从顶点i到顶点j的最短路径长度大于前一阶段中从顶点i到顶点k再到顶点j的路径长度，那么就需要修改当前阶段中顶点i到顶点j的最短路径长度为前一阶段的顶点i到顶点k再到顶点j的路径长度，并把当前阶段的顶点i到顶点j的中转顶点修改为顶点k，除此之外不需要修改
当然了，对于矩阵A里的所有元素都需要循环的遍历一遍进行判断，

如上图，开始0号阶段，

基于-1号阶段（初始化阶段）求得的矩阵信息即A(-1)和path(-1)，求解0号阶段的最优矩阵即A(0)和path(0)，求解的方法如上图左下角的公式，

0号阶段允许v0顶点作为各个顶点对之间的中转顶点，那么最短路径会不会有进一步的优化？

需要遍历-1号阶段（初始化阶段）的矩阵A(-1)，对矩阵A(-1)中的每一个元素都进行上述图片中左下角公式的检查，

比如v2到v1的路径，在-1号阶段（初始化阶段）的A矩阵中，对应A矩阵的v2行v1列即A(-1)[2] [1]，A(-1)[2] [1]的值为无穷即v2到v1没有直达的路径，-1号阶段中v2到v1没有中转顶点且v2无法直达v1，现在0号阶段中允许v0作为中转点，因此可以先从v2到达v0，再从v0到达v1，由图可知这条路径的长度为11，比-1号阶段找到的路径长度为无穷更短，所以需要把v2到v1的最短路径长度更新为11，即A(0)[2] [1]为11，由于此时v0作为v2到v1的中转顶点，所以还需要把path(0)[2] [1]赋值为0，代表从v2到v1需要v0作为中转顶点，其他顶点对以此类推，

从-1号阶段（初始化阶段）到0号阶段，经过所有的检查之后，需要修改的数据只有v2到v1的路径信息，如下图：

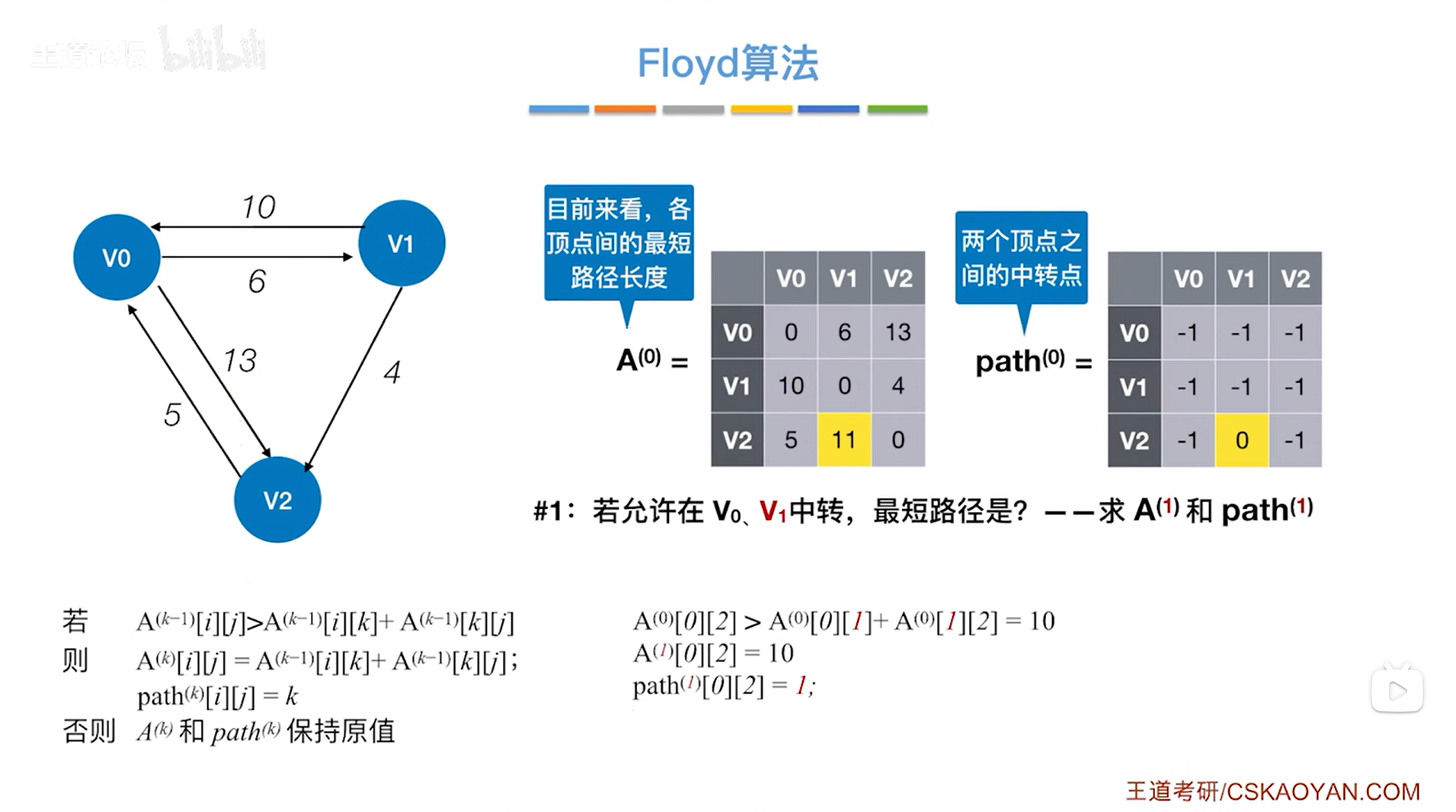
如上图，开始1号阶段，

基于0号阶段求得的矩阵信息即A(0)和path(0)，求解1号阶段的最优矩阵即A(1)和path(1)，

1号阶段在允许v0顶点作为各个顶点对之间的中转顶点的基础上，允许v1顶点也作为各个顶点对之间的中转顶点，那么最短路径会不会有进一步的优化？

需要遍历0号阶段的矩阵A(0)，对矩阵A(0)中的每一个元素都进行上述图片中左下角公式的检查，

比如v0到v2的路径，在0号阶段的A矩阵中，对应A矩阵的v0行v2列即A(0)[0] [2]，A(0)[0] [2]的值为13即0号阶段能够找到的v0到v2的最短路径为13，0号阶段中v0到v2没有中转顶点即v0直达v2，现在1号阶段中允许v1作为中转顶点，因此可以先从v0到达v1，再从v1到达v2，由图可知这条路径的长度为10，比0号阶段找到的路径长度13更短，所以需要把v0到v2的最短路径长度更新为10，即A(1)[0] [2]为10，由于此时v1作为v0到v2的中转顶点，所以还需要把path(1)[0] [2]赋值为1，代表从v0到v2需要v1作为中转顶点，其他顶点对以此类推，

从0号阶段到1号阶段，经过所有的检查之后，需要修改的数据只有v0到v2的路径信息，如下图：

如上图，开始2号阶段，

基于1号阶段求得的矩阵信息即A(1)和path(1)，求解2号阶段的最优矩阵即A(2)和path(2)，

2号阶段在允许v0、v1顶点作为各个顶点对之间的中转顶点的基础上，允许v2顶点也作为各个顶点对之间的中转顶点，那么最短路径会不会有进一步的优化？

需要遍历1号阶段的矩阵A(1)，对矩阵A(1)中的每一个元素都进行上述图片中左下角公式的检查，

比如v1到v0的路径，在1号阶段的A矩阵中，对应A矩阵的v1行v0列即A(1)[1] [0]，A(1)[1] [0]的值为10即1号阶段能够找到的v1到v0的最短路径为10，1号阶段中v1到v0没有中转顶点即v1直达v0，现在2号阶段中允许v2作为中转顶点，因此可以先从v1到达v2，再从v2到达v0，由图可知这条路径的长度为9，比1号阶段找到的路径长度10更短，所以需要把v1到v0的最短路径长度更新为9，即A(2)[1] [0]为9，由于此时v2作为v1到v0的中转顶点，所以还需要把path(2)[1] [0]赋值为2，代表从v1到v0需要v2作为中转顶点，其他顶点对以此类推，

从1号阶段到2号阶段，经过所有的检查之后，需要修改的数据只有v1到v0的路径信息，如下图：

如上图，至此总共经历了3轮的递推，由此可以推出若图中顶点总数为n，那么经过n轮递推就可以得到最终的A(n-1)矩阵和path(n-1)矩阵，

在每一轮的递推中都会增加一个新的顶点作为顶点对之间的中转顶点，

对于本例，基于最终得出的A(2)和path(2)就可以得到任意两个顶点对之间的最短路径长度和最短路径的信息，

例一：要找出v1到v2的最短路径的信息，通过A矩阵可以得出v1到v2的最短路径长度为4（A(2)[1] [2]的值为4），通过path矩阵可以得出v1到v2之间没有中转顶点（path(2)[1] [2]的值为-1）->v1到v2的最短路径长度为4，v1到v2的最短路径信息为v1->v2；

例二：要找出v0到v2的最短路径的信息，通过A矩阵可以得出v0到v2的最短路径长度为10（A(2)[0] [2]的值为10），通过path矩阵可以得出v0到v2之间的中转顶点为v1（path(2)[0] [2]的值为1）->v0到v2的最短路径长度为10，v0到v2的最短路径信息为v0->v1->v2；

例三：要找出v1到v0的最短路径的信息，通过A矩阵可以得出v1到v0的最短路径长度为9（A(2)[1] [0]的值为9），通过path矩阵可以得出v1到v0之间的中转顶点为v2（path(2)[1] [0]的值为2）->v1到v0的最短路径长度为9，v1到v0的最短路径信息为v1->v2->v0，

所以这就是A矩阵和path矩阵的用法，如下图：

虽然刚才分析Floyd算法的过程看起来比较复杂，但是这个算法用代码实现的话很简单。

2.核心代码：

图示：

准备工作中要根据图的信息初始化矩阵A和矩阵path，

矩阵A就是图的邻接矩阵，path矩阵初始阶段全部赋值为-1，

接下来每一轮的处理当中都会新增加一个顶点Vk作为顶点对之间的中转顶点，

图中总共有n个顶点，因此最外层的循环就需要循环n次，对于最外层的每一层循环中每当新增加一个中转顶点时，都需要检查矩阵A中的所有元素，因此就需要把A矩阵的所有的行和列都扫描一遍，对于矩阵A的任何一个元素都需要进行一个判断A[i] [j]>A[i] [k]+A[k] [j]，满足if条件就执行if语句，更新最短路径长度，更新中转顶点信息，除此之外不动。

代码：

//......准备工作，根据图的信息初始化矩阵A和矩阵path/* 矩阵A：使用了图的邻接矩阵，图的邻接矩阵的代码实现详情见6.2.图的存储结构-邻接矩阵法 矩阵path：记录顶点对之间的中转顶点 */for( int k=0 ; k<n ; k++ ) //依次考虑以Vk作为中转顶点，k为中转顶点的编号，从V0即第一个顶点开始，要进行n轮，因为图中共有n个顶点 {for( int i=0 ; i<n ; i++ ) //开始遍历整个A矩阵，i为行号，j为列号 {for( int j=0 ; j<n ; j++ ){if( A[i][j] > A[i][k]+A[k][j] ) //如果以Vk为中转顶点的路径更短 {A[i][j] = A[i][k]+A[k][j]; //更新最短路径长度path[i][j] = k; //添加中转顶点编号 }}}}

3.核心代码性能分析：

如上图，假设图中共有n个顶点，

由代码可知最外层循环有n轮，每一层的循环都会循环n * n次，因此该算法的时间复杂度为O( |n| * |n| * |n| )，

由于该算法需要建立两个矩阵即A矩阵和path矩阵来完成，这两个矩阵的大小都是n行n列，所以空间复杂度为O( 2 * |n| * |n| )，等价于O( |n| * |n| )。

结论：假设图中共有V个顶点，那么Floyd算法的时间复杂度为O( |V| * |V| * |V| )，空间复杂度为O( |V| * |V| )。

（之前分析的例子只有3个顶点，所以当加入某一个顶点作为中转顶点时，会发现路径最多也就是经过两条边，所以这个例子有助于理解Floyd算法，但是该例子对于Floyd算法的真正作用无法体现出来）

三.Floyd算法较复杂的例子：

1.演示：

如上图，以上述图片的有向图为例，现在求图中各个顶点对之间的最短路径，

开始-1号阶段（初始化阶段），如下图：

如上图，需要初始化两个矩阵即两个二维数组，第一个矩阵是A矩阵，第二个矩阵是path矩阵，

第一个矩阵即A矩阵就是该图的邻接矩阵，矩阵A表示就目前来看，能找到的各个顶点对之间的最短路径长度是多少，初始阶段是不允许各个顶点对之间的路径存在中转顶点，所以就目前来看，比如v0到v2的最短路径长度就是1，因为现在这个阶段是不允许以任何顶点作为中转顶点加入的，因此v0行v2列的值为1；

如下图：

如上图，左下角的公式就是求从k-1阶段（前一阶段）到k阶段（当前阶段）中A矩阵和path矩阵的公式，该公式解读如下：

k代表当前阶段，也代表当前中转顶点的编号；k-1代表前一个阶段
A(k-1)[i] [j]表示前一个阶段的A矩阵中顶点i到顶点j的最短路径长度
A(k-1)[i] [k]表示前一个阶段的A矩阵中顶点i到顶点k的路径长度
A(k-1)[k] [j]表示前一个阶段的A矩阵中顶点k到顶点j的路径长度
A(k-1)[i] [k]+A(k-1)[k] [j]就表示前一个阶段的A矩阵中顶点i到中转顶点k再到顶点j的路径长度
A(k)[i] [j]=A(k-1)[i] [k]+A(k-1)[k] [j]表示把前一个阶段的A矩阵中顶点i到中转顶点k再到顶点j的路径长度赋值给当前阶段的A矩阵中顶点i到顶点j的最短路径长度
path(k)[i] [j]=k就表示当前阶段中从顶点i到顶点j的路径中中转顶点为顶点k
因此上图左下角的公式A(k-1)[i] [j]>A(k-1)[i] [k]+A(k-1)[k] [j]就表示如果前一个阶段的A矩阵中顶点i到顶点j的最短路径长度大于前一个阶段的A矩阵中顶点i到中转顶点k再到顶点j的路径长度，那么就执行A(k)[i] [j]=A(k-1)[i] [k]+A(k-1)[k] [j]，且修改path的值为path(k)[i] [j]=k
A(k)和path(k)保持原值就是对应顶点A(k)等于A(k-1)，path(k)等于path(k-1)
总而言之，就是如果前一阶段中从顶点i到顶点j的最短路径长度大于前一阶段中从顶点i到顶点k再到顶点j的路径长度，那么就需要修改当前阶段中顶点i到顶点j的最短路径长度为前一阶段的顶点i到顶点k再到顶点j的路径长度，并把当前阶段的顶点i到顶点j的中转顶点修改为顶点k，除此之外不需要修改
当然了，对于矩阵A里的所有元素都需要循环的遍历一遍进行判断，

如上图，开始0号阶段即k为0时，

基于-1号阶段（初始化阶段）求得的矩阵信息即A(-1)和path(-1)，求解0号阶段的最优矩阵即A(0)和path(0)，求解的方法如上图左下角的公式，

0号阶段允许v0顶点作为各个顶点对之间的中转顶点，那么最短路径会不会有进一步的优化？

需要遍历-1号阶段（初始化阶段）的矩阵A(-1)，对矩阵A(-1)中的每一个元素都进行上述图片中左下角公式的检查，

也可以结合图可知，由于图中任意一个顶点都没有直接指向v0的，所以如果某个顶点要经过v0，那么路径长度必然为无穷，显然不会比之前已找到的路径更短，因此也就不会发生任何数据的修改，

从-1号阶段（初始化阶段）到0号阶段，经过所有的检查之后，所有数据都不需要修改，如下图：

如上图，开始1号阶段即k为1时，

基于0号阶段求得的矩阵信息即A(0)和path(0)，求解1号阶段的最优矩阵即A(1)和path(1)，

1号阶段在允许v0顶点作为各个顶点对之间的中转顶点的基础上，允许v1顶点也作为各个顶点对之间的中转顶点，那么最短路径会不会有进一步的优化？

需要遍历0号阶段的矩阵A(0)，对矩阵A(0)中的每一个元素都进行上述图片中左下角公式的检查，

比如v2到v3的路径，在0号阶段的A矩阵中，对应A矩阵的v2行v3列即A(0)[2] [3]，A(0)[2] [3]的值为无穷即0号阶段能够找到的v2到v3的最短路径为无穷（0号阶段v2到v3没有明确的路径），0号阶段中v2到v3也没有中转顶点，现在1号阶段中允许v1作为中转顶点，因此可以先从v2到达v1，再从v1到达v3，由图可知这条路径的长度为2，比0号阶段找到的路径长度无穷更短，所以需要把v2到v3的最短路径长度更新为2，即A(1)[2] [3]为2，由于此时v1作为v2到v3的中转顶点，所以还需要把path(1)[2] [3]赋值为1，代表从v2到v3需要v1作为中转顶点，其他顶点对以此类推->可知v2到v4的路径信息也需要修改，

从0号阶段到1号阶段，经过所有的检查之后，修改后的矩阵信息如下图：

如上图，开始2号阶段即k为2时，

基于1号阶段求得的矩阵信息即A(1)和path(1)，求解2号阶段的最优矩阵即A(2)和path(2)，

需要遍历1号阶段的矩阵A(1)，对矩阵A(1)中的每一个元素都进行上述图片中左下角公式的检查，

比如v0到v1的路径，在1号阶段的A矩阵中，对应A矩阵的v0行v1列即A(1)[0] [1]，A(1)[0] [1]的值为无穷即1号阶段能够找到的v0到v1的最短路径为无穷（1号阶段v0到v1没有明确的路径），1号阶段中v0到v1没有中转顶点，现在2号阶段中允许v2作为中转顶点，因此可以先从v0到达v2，再从v2到达v1，由图可知这条路径的长度为2，比1号阶段找到的路径长度无穷更短，所以需要把v0到v1的最短路径长度更新为2，即A(2)[0] [1]为2，由于此时v2作为v0到v1的中转顶点，所以还需要把path(2)[0] [1]赋值为2，代表从v0到v1需要v2作为中转顶点，其他顶点对以此类推

->通过上述图片中左下角的公式可知v0到v3的路径信息也需要修改，1号阶段中v0到v3的最短路径长度为无穷（1号阶段中v0到v3没有明确的路径），但是现在允许v2作为中转顶点，那么可以通过路径A(1)[0] [2]+A(1)[2] [3]（注意：A(1)[0] [2]表示1号阶段中v0到v2的路径长度，A(1)[0] [2]的值为1即v0到v2的路径长度为1；A(1)[2] [3]表示1号阶段中v2到v3的路径长度，A(1)[2] [3]的值为2即v2到v3的路径长度为2，但是通过图可以发现，v2无法直达v3，但实际上v2到v3的最短路径信息在1号阶段就已经更新过了，v2到v3还需要再经过顶点v1，所以v2到v3的路径信息为v2->v1->v3），此时v0到v3的路径总长度为3，比1号阶段找到的路径长度无穷更短，所以需要把v0到v3的最短路径长度更新为3，即A(2)[0] [3]为3，由于此时v2作为v0到v3的中转顶点，所以还需要把path(2)[0] [3]赋值为2，代表从v0到v3需要v2作为中转顶点，

所以在这个地方也考虑到之前增加了v1作为中转顶点，现在的计算是基于之前的最优结果再增加一个v2作为中转顶点，所以2号阶段新找到的v0到v3的最短路径，完整的信息是v0->v2->v1->v3，整个路径当中其实已经考虑到可以以v2、v1、v0这些顶点作为中转顶点的情况

->同理v0到v4的路径信息也需要修改，

从1号阶段到2号阶段，经过所有的检查之后，修改后的矩阵信息如下图：

如上图，开始3号阶段即k为3时，

基于2号阶段求得的矩阵信息即A(2)和path(2)，求解3号阶段的最优矩阵即A(3)和path(3)，

3号阶段在允许v0、v1、v2顶点作为各个顶点对之间的中转顶点的基础上，允许v3顶点也作为各个顶点对之间的中转顶点，那么最短路径会不会有进一步的优化？

需要遍历2号阶段的矩阵A(2)，对矩阵A(2)中的每一个元素都进行上述图片中左下角公式的检查，

经过所有的检查之后，v0到v4的路径信息、v1到v4的路径信息、v2到v4的路径信息需要修改，

从2号阶段到3号阶段，修改后的矩阵信息如下图：

如上图，开始4号阶段即k为4时，

基于3号阶段求得的矩阵信息即A(3)和path(3)，求解4号阶段的最优矩阵即A(4)和path(4)，

4号阶段在允许v0、v1、v2、v3顶点作为各个顶点对之间的中转顶点的基础上，允许v4顶点也作为各个顶点对之间的中转顶点，那么最短路径会不会有进一步的优化？

需要遍历3号阶段的矩阵A(3)，对矩阵A(3)中的每一个元素都进行上述图片中左下角公式的检查，

经过所有的检查之后，没有路径信息需要修改，

从3号阶段到4号阶段，修改后的矩阵信息如下图：

如上图，得出的最终矩阵A(4)和path(4)，从0号阶段开始到4号阶段共进行了五轮操作（图中共有5个顶点，初始化阶段不算），最终得出的矩阵A和矩阵path如下图：（图中共有几个顶点，那么几轮就能得出最终的矩阵）

2.得出的A矩阵和path矩阵的运用：

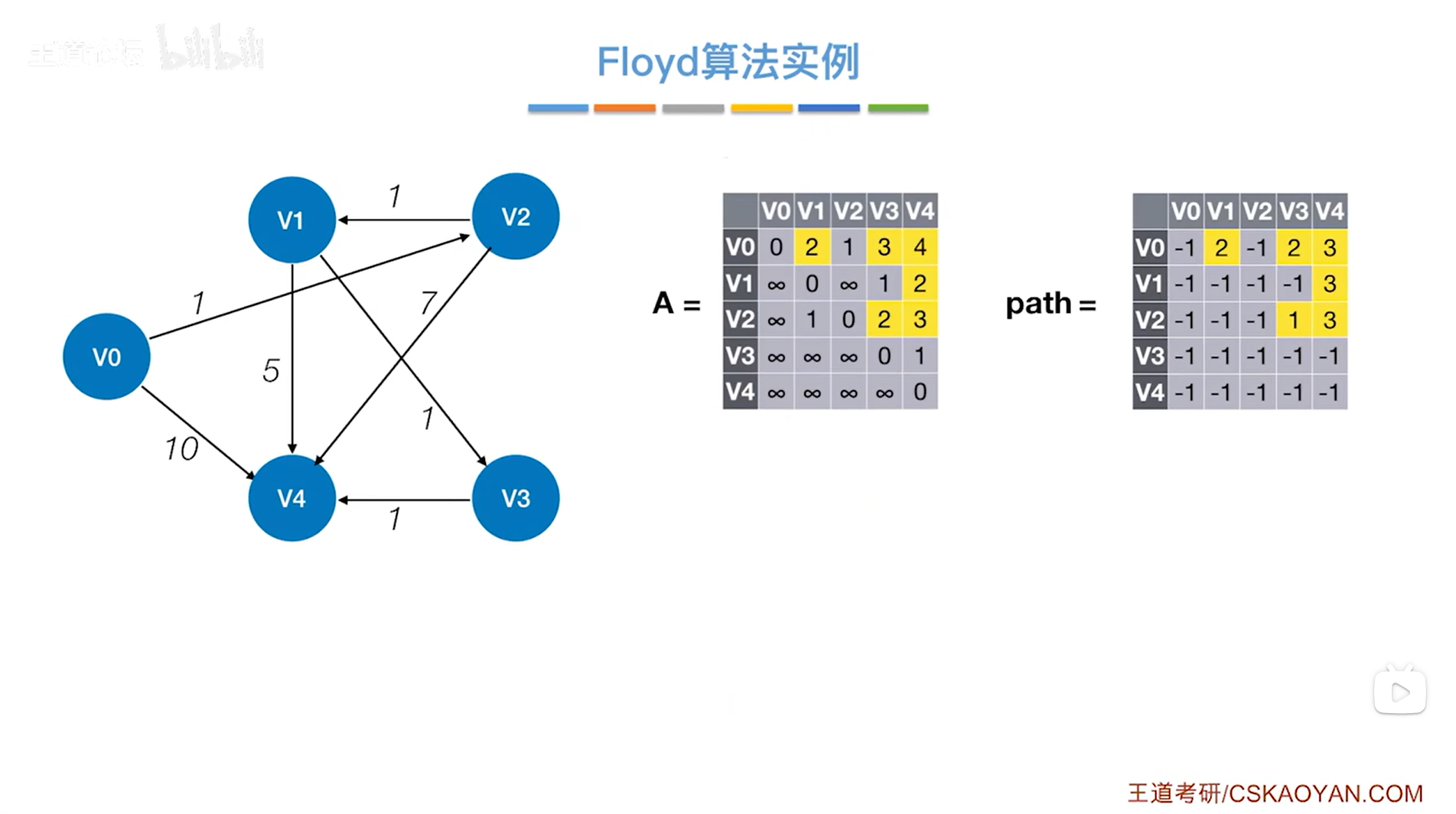
如上图，接下来演示如何使用A矩阵和path矩阵来找顶点对之间的最短路径信息，

比如找v0到v4的最短路径信息，

通过矩阵A里v0行v4列即A[0] [4]可知v0到v4的最短路径长度为4，

通过矩阵path可得出v0到v4的完整的路径过程：

步骤一：通过矩阵path里v0行v4列即path[0] [4]可知v0到v4的中转顶点是v3顶点->（v0 v3 v4），如下图

步骤二：通过矩阵path里v0行v3列即path[0] [3]可知v0到v3的中转顶点是v2顶点->（v0 v2 v3 v4），如下图

步骤三：通过矩阵path里v3行v4列即path[3] [4]可知v3可以直达v4顶点->（v0 v2 v3->v4），如下图

步骤四：通过矩阵path里v0行v2列即path[0] [2]可知v0可以直达v2顶点->（v0->v2 v3->v4）

步骤五：通过矩阵path里v2行v3列即path[2] [3]可知v2到v3的中转顶点是v1顶点->（v0->v2 v1 v3->v4）

步骤六：通过矩阵path里v2行v1列即path[2] [1]可知v2可以直达v1顶点->（v0->v2->v1 v3->v4）

步骤七：通过矩阵path里v1行v3列即path[1] [3]可知v1可以直达v3顶点->（v0->v2->v1->v3->v4）

所以完整的路径过程为v0->v2->v1->v3->v4，如下图：

如上图，通过path矩阵得出了顶点对之间完整的路径信息，

推导路径信息的过程可以使用递归算法进行实现，递归思路：用二叉树实现，以新添加的中转顶点为根结点，左子树递归检查左边的路径，右子树递归检查右边的路径，每一层递归结束的条件就是顶点对之间可以直达即path值为-1，

本例中A矩阵有5行5列，通过之前的分析，总共需要5 * 5 *5等于125次的检查。

四.Floyd算法适用于负权值带权图：

五.Floyd算法无法解决的问题：

这一类的问题称为带有“负权回路”的图，

比如上述图片的例子，v0到v1之间的边是负权值，v1到v2之间的边和v2到v0之间的边都是正权值，v0到v1之间的边、v1到v2之间的边、v2到v0之间的边组成了一个完整的回路，

对于该图来说，如果要求v0到v1的最短路径，如果是v0->v1，那么路径长度为-9；如果是v0->v1->v2->v0->v1，那么路径长度为-11，以此类推，会发现这个回路走的越多，最终v0到v1的路径长度会越小，因为v1->v2->v0的路径长度总和为7，而v0->v1的路径长度总和为-9，从v0出发，以v1为终点，每走完一圈环路，路径总长度就会减2，因此v0到v1的路径总长度会一直减小，最终会导致这种类型的图根本找不到所谓的最短路径。