理论解释:
1. 目标
假设 a = 3.14159,我们想四舍五入到 小数点后两位(即 3.14 或 3.15)。
2. 步骤拆解
(1) a * 100
- 把
a放大 100 倍,让小数点后两位变成整数部分: -
3.14159 * 100 = 314.159(2)
+ 0.5 - 关键步骤:如果小数部分 ≥ 0.5,则整数部分 +1:
-
314.159 + 0.5 = 314.659 -
如果原数是 3.146(即 314.6),则:
-
314.6 + 0.5 = 315.1(3)
(int)强制截断 - 强制转换为
int会 丢弃小数部分(不是四舍五入,而是直接截断): -
(int)314.659 = 314 (int)315.1 = 315这样:
- 314.159 → 314(因为 0.659 < 1,相当于 3.14159 舍去)
- 314.6 → 315(因为 0.1 < 1,但整数部分已经是 315,相当于 3.146 进位)
(4) / 100.0
- 最后缩小 100 倍,恢复原来的数量级:
-
314 / 100.0 = 3.14 315 / 100.0 = 3.153. 为什么能保证精确?
- 浮点数存储可能不精确(如
3.145可能存储为3.144999999...),直接用%.2f可能会错误舍入。 (int)(x + 0.5)是经典的“四舍五入”方法,不依赖浮点数的内部表示,而是利用整数截断特性,确保:- 小数部分 ≥ 0.5 → 进位
- 小数部分 < 0.5 → 舍去
例题:
代码如下:
错误示例
(1)
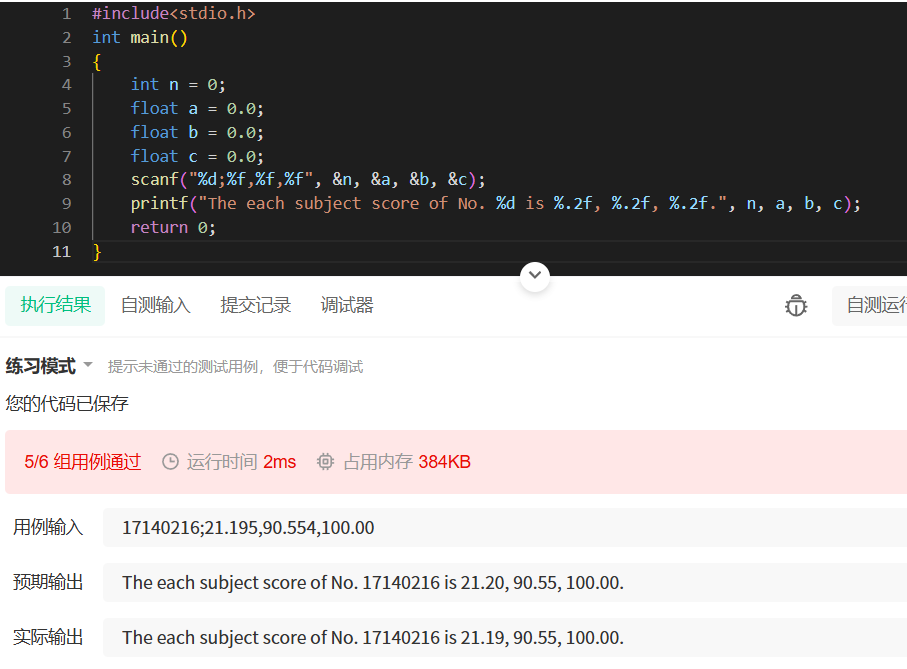
(2)

(3)

正确代码:






