Map & Set 常用的集合类
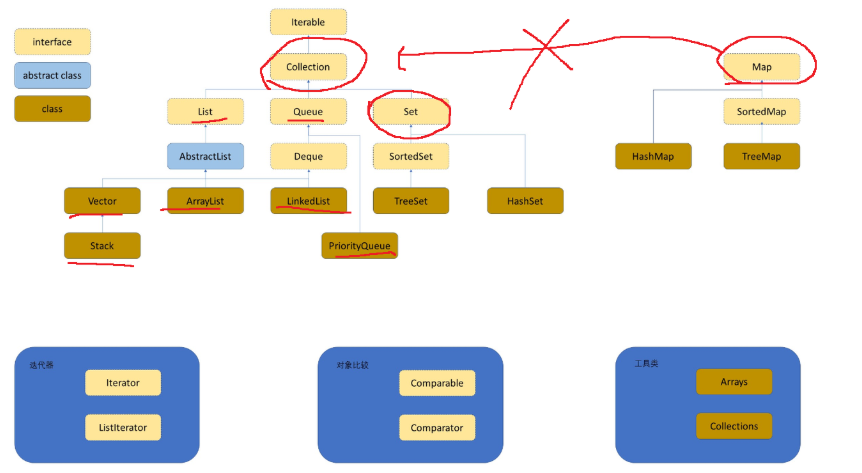
Set 实现了 Collection, Map并没有实现
Set 的核心特点:
1.保存的元素 无序
2.保存的元素不能修改
3.保存的元素不会重复
Set 啥意思?
封装 => 给私有成员提供 get set 方法
集合类 => Set 集合(数学上谈到的集合), 数学上集合的特点就是,不能重复
前面谈到的 List 是有序的(顺序是具有一定相关性的)
有两个 List: {1,2,3}; List: {1,3,2},认定这两个 List 是不等价的
但是 Set 是无序 的
有两个 Set: {1,2,3}; Set: {1,3,2} 让定这两 Set 是等价的
和 Set 非常相似,Map 更进一步; Set 上面保存的只是 "键", Map 上保存的是"键值对"(key - value)
Set 只是一个接口,需要创建实现 Set 的类
public interface Set<E> extends Collection<E>Set<String> set = new TreeSet<>();
Set<String> set2 = new HashSet<>();TreeSet 是树状结构(二叉树,有很大关联的)
HashSet 哈希表
Set 中是没有"下标"概念的, Set 最主要的应用场景,就是用来看元素是否在 Set 中存在的(录取名单,就相当于是 Set)
map.put("及时雨","宋江");
map.put("黑旋风","李逵");
map.put("小李广","华荣");map 中组织的元素顺序也是"无序"的,无论你插入的顺序如何,最终保存元素的顺序都是一定的.
把 map 想象成比 Set 更进一步
对于 map 来说, key 是唯一的, key 是无序的, 对于 value 来说,没有要求(key 不能修改)
map.put("小李广","华荣");
map.put("小李广","华声");在 put 的时候,如果 key 已经存在, 此时就会对 value 进行修改,而不是新增键值对
keySet 是把所有的 key,收集起来放到一个 Set 中
entrySet 是把所有的 key - value 收集起来放到一个 Set 中
entry 是啥意思?? 入口
和 keySet 一样,entrySet 也是一个高开销的操作,也需要慎用(不能针对很大的 Map 进行 entrySet)
Map 设计的初心,是让你解决 key => value 的映射问题.而不是让你用来遍历的, 数据结构之所以有这么多,各有侧重点
Set 的核心操作: add, remove, contains
Map的核心操作:get, put, remove
二叉搜索树(Binary Search Tree)
二叉搜索树,在二叉树的基础上, 做出了额外的要求:
如果左子树不为空, 左子树的所有 key, 都应该小于根节点的 key
如果右子树不为空, 右子树的所有 key 都应该大于等于根节点的 key
二叉搜素树和堆都是特殊的二叉树, 也都有"大小关系"的要求
二叉搜索树,是存在"左右关系"的要求,左<根<右,堆,是存在"上下关系"的要求,父节点 < 子节点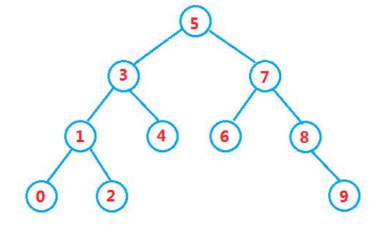
如果要进行查找,就可以用类似于"二分"的方式来进行
数组的二分查找,分出来的是两个部分,是"均匀"对于二叉搜索树来说,就不一定了.(二叉搜索树的左右子树包含的节点数可能不同,而且可能存在比较大的差异)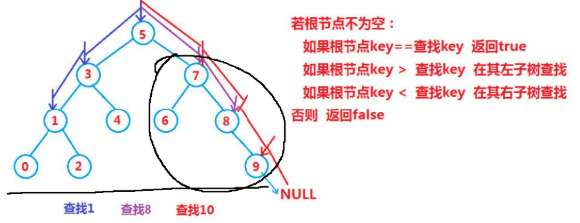
理想情况下,如果二叉搜索树,左右子树的个数都差不多,这个时候,此时的时间复杂度O(logN),二叉搜索树查找,关键的操作就是比较次数,比较次数和树的高度有关系, 如果二叉树左右子树比较均衡,高度就是 logn,如果出现不理想的极端情况,单枝树的情况,此时的查找就和链表的遍历差不多了,因此此时的时间复杂度是O(n)
对于二叉树来说,插入的本质,还是查找,通过查找的方式,确定新元素的所在位置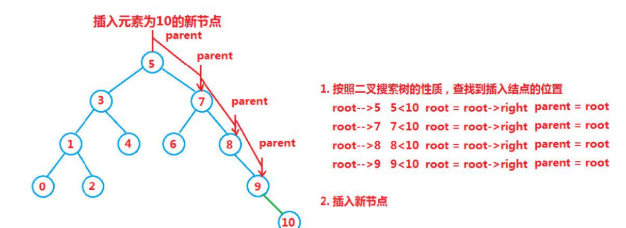
删除操作是二叉树搜索中比较复杂的了
首先,需要先查找节点所在的位置.不光要记录要删除节点(cur)的位置,也需要记录节点的父节点(parent)的位置
1.如果 cur 没有子树,直接删除 cur 即可.
修改 parent 的引用,此时 需要注意到 cur 是 parent 的左子树还是右子树
if(cur == parent.left) {parent.left = null;
} else {parent.right = null;
}2.如果 cur 只有左子树,没有右子树,此时就可以把 cur 的左子树,接到 parent 上
if(cur == parent.left) {parent.left = cur.left;
} else {parent.right = cur.right;
}






