1、简介
在评估机器学习模型的性能时,根据任务的不同(分类、回归等),我们可以使用不同的评价指标。本文主要是介绍一些常见的评估指标及其优缺点。
2、回归模型指标
2.1. 平均绝对误差(MAE, Mean Absolute Error)
-
定义:预测值与真实值的绝对误差的平均值。
-
计算公式:
-

-
变量:
-
n:样本数量
-
yi:真实值
-
y^i:预测值
-
-
优点:
-
直观易解释,与数据单位一致,因为它直接给出了预测值与真实值之间的平均绝对差异。
-
对异常值不敏感(鲁棒性强)。
-
-
缺点:
-
无法反映误差的方向(高估或低估)。
-
不适用于需要强调大误差的场景。
-
2.2. 均方误差(MSE, Mean Squared Error)
-
定义:预测值与真实值的平方误差的平均值。
-
计算公式:
-

-
优点:
-
对大误差惩罚更重,适合重视显著错误的场景。
-
MSE放大了较大误差的影响,有助于识别出异常值对模型的影响。
-
-
缺点:
-
单位与数据不一致(平方单位),难以直观理解。
-
对异常值敏感。
-
2.3. 均方根误差(RMSE, Root Mean Squared Error)
-
定义:MSE 的平方根,恢复单位一致性。
-
计算公式:
-

-
优点:兼具 MSE 对大误差敏感的特点,且单位与数据一致。
-
缺点:仍对异常值敏感。
2.4. R²(决定系数)
-
定义:模型解释变量变化的百分比,取值区间 [0, 1]。
-
计算公式:
-

-
变量:
-
SSE:残差平方和(预测误差平方和)
-
SST:总平方和(真实值的方差)
-
yˉ:真实值的均值
-
-
优点:
-
标准化指标,便于比较不同模型。
-
-
缺点:
-
随模型复杂度增加可能虚高(过拟合时仍表现良好)。
-
无法直接反映预测误差大小。
-
2.5. 调整R²(Adjusted R²)
-
定义:考虑自变量数量的调整版 R²。
-
计算公式:
-

-
优点:惩罚无关变量,避免过拟合。
-
缺点:仍无法完全解决 R² 的局限性。
3、回归模型指标
3.1. 准确率(Accuracy)
-
定义:正确预测样本占总样本的比例。
-
计算公式:

-
变量(混淆矩阵):
-
TP(True Positive):正确预测的正类
-
TN(True Negative):正确预测的负类
-
FP(False Positive):负类误判为正类
-
FN(False Negative):正类误判为负类
-
-
优点:简单直观,适合于类别分布均衡的数据集。
-
缺点:
-
类别不平衡时误导性高(如 99% 负类时全预测负类准确率达 99%)。
-
3.2. 混淆矩阵衍生指标
-
精确率(Precision):预测为正的样本中实际为正的比例。
- 计算公式:

-
优点:关注减少假阳性(如垃圾邮件检测)。
-
缺点:忽略假阴性。
- 计算公式:
-
召回率(Recall/Sensitivity):实际为正的样本中被正确预测的比例。
-
计算公式:

-
优点:关注减少假阴性(如疾病诊断)。
-
缺点:忽略假阳性。
-
-
F1分数:精确率和召回率的调和平均。
-
计算公式:

-
优点:平衡二者,适合类别不平衡数据。
-
缺点:假设精确率和召回率同等重要。
-
3.3. ROC-AUC
-
定义:ROC 曲线下面积,评估模型在不同阈值下的性能。
-
计算公式:横轴为假正率(FPR),纵轴为真正率(TPR)
-

-
优点:
-
与类别分布无关,适合不平衡数据。
-
综合反映模型整体排序能力。
-
提供了一个全面的视角来评估分类器的整体性能,不受阈值选择的影响。
-
-
缺点:
-
对概率校准不敏感。
-
高 AUC 不保证高精确率或召回率。
-
提供了一个全面的视角来评估分类器的整体性能,不受阈值选择的影响。
-
3.4. PR-AUC(精确率-召回率曲线下面积)
-
优点:在不平衡数据中比 ROC-AUC 更敏感。
-
缺点:解释复杂度较高。
3.5. 对数损失(Log Loss)
-
定义:基于预测概率的损失函数。
-
计算公式:
-
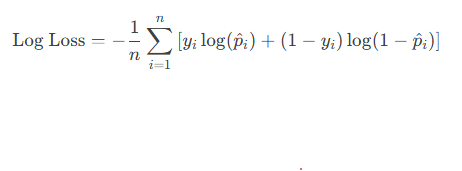
-
变量:
-
p^i:预测样本为正类的概率
-
yi∈{0,1}:真实标签
-
-
优点:对概率校准敏感,适合概率模型。
-
缺点:对错误预测惩罚较重,可能导致数值不稳定。
3.6. 马修斯相关系数(MCC)
-
计算公式:
-

-
优点:综合考虑所有混淆矩阵值,适用于不平衡数据。
-
缺点:计算复杂,解释性较差。
3.7.Cohen's Kappa
- 优点: 考虑到了随机猜测的可能性,提供了比准确率更稳健的评估。
- 缺点: 计算复杂度较高,不易于快速解读。
4、其他任务指标
4.1. 聚类
-
轮廓系数(Silhouette Coefficient):衡量聚类紧密度和分离度。
- 计算公式:
-

-
优点:无需真实标签。
-
缺点:计算复杂度高,不适用于大规模数据。
-
4.2. 自然语言处理(NLP)
-
BLEU/ROUGE:评估生成文本与参考文本的相似度。
- 计算公式:
-

-
变量:
-
pk:n-gram(如1-gram到4-gram)的精确率
-
BP:简洁惩罚因子(避免短句得分过高)
-
-
-
优点:自动化评估生成质量。
-
缺点:忽略语义和逻辑一致性。
-
4.3. 推荐系统
-
NDCG(归一化折损累积增益):衡量排序质量。
- 计算公式:
-

-
优点:考虑位置权重和相关性分级。
-
缺点:计算复杂。
-
5、选择指标的建议
-
任务类型:优先选择与任务匹配的指标(如回归用 RMSE,分类用 F1)。
-
数据分布:类别不平衡时避免准确率,选择 F1、AUC 或 MCC。
-
业务需求:根据场景调整(如医疗诊断重视召回率,反欺诈重视精确率)。
通过结合多个指标,可以更全面地评估模型性能。


)



