“傅里叶变换算法”来检测货物外形损坏
要使用傅里叶变换算法来检测货物外形损坏,首先需要理解基本概念。傅里叶变换是一种数学变换,用于将信号从时域(或空间域)转换到频域。在图像处理中,二维傅里叶变换可以用来分析图像的频率成分。然而,直接用傅里叶变换来检测货物外形损坏并不是最常见的方法,因为傅里叶变换主要用于分析周期性和重复性模式,而外形损坏通常是局部、非周期性的。

尽管如此,我们可以通过以下步骤尝试实现一个基于傅里叶变换的简单示例程序,用于检测货物外形是否有明显的异常(例如断裂、缺失部分等)。这个程序将会:
- 读取实时视频流。
- 对每一帧进行处理,将其转换为灰度图像。
- 使用二维傅里叶变换来分析图像的频率分量。
- 基于频率信息识别可能的异常。
- 显示处理结果。
下面是一个简化的Python代码示例,演示了如何使用OpenCV和NumPy库来实现上述过程。请确保你已经安装了opencv-python和numpy库。
import cv2
import numpy as npdef process_frame(frame):# 将帧转换为灰度图像gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)# 进行二维傅里叶变换f_transform = np.fft.fft2(gray)f_transform_shifted = np.fft.fftshift(f_transform)# 计算幅度谱magnitude_spectrum = 20 * np.log(np.abs(f_transform_shifted))# 简单的异常检测逻辑:假设低频区域的能量应该较高,# 如果某个区域的能量低于阈值,则认为可能是异常。threshold = 150mask = magnitude_spectrum < threshold# 将异常区域标记出来frame_with_mark = frame.copy()frame_with_mark[mask] = [0, 0, 255] # 异常区域标记为红色return frame_with_mark, magnitude_spectrum# 打开视频捕获设备(这里使用默认摄像头)
cap = cv2.VideoCapture(0)while True:ret, frame = cap.read()if not ret:breakframe_with_mark, magnitude_spectrum = process_frame(frame)# 显示原图以及经过傅里叶变换后的幅度谱cv2.imshow('Original with Mark', frame_with_mark)cv2.imshow('Magnitude Spectrum', magnitude_spectrum)if cv2.waitKey(1) & 0xFF == ord('q'):break# 完成后释放资源
cap.release()
cv2.destroyAllWindows()


请注意,这只是一个非常基础的示例,实际应用中可能需要更复杂的算法来准确地检测货物外形损坏。此外,考虑到傅里叶变换并非专门针对这种类型的图像分析设计,您可能还会考虑其他技术,如边缘检测、形态学操作或其他高级图像处理技术。

傅里叶变换在图像处理中的应用有哪些?
傅里叶变换在图像处理中有着广泛的应用,主要用于分析和处理图像的频率成分。以下是傅里叶变换在图像处理中的几个主要应用:
-
频域滤波:
- 低通滤波:通过去除高频分量(如噪声)来平滑图像。这有助于减少图像中的细节和噪声,同时保留大范围的结构信息。
- 高通滤波:通过去除低频分量来增强图像的边缘和其他细节。这种技术可以用于突出显示图像中的边界和纹理。
-
图像压缩:
傅里叶变换(特别是离散余弦变换DCT,它是傅里叶变换的一种形式)是许多图像压缩算法的基础,比如JPEG格式。通过转换到频域,可以识别并移除那些对人类视觉影响较小的频率分量,从而实现有效的压缩。 -
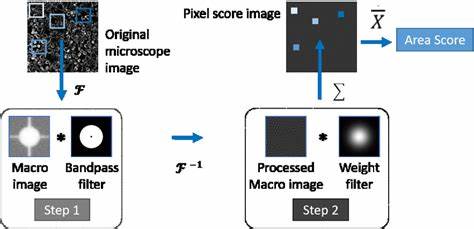
特征提取:
在模式识别和计算机视觉领域,可以通过分析图像的频率特性来提取有用的特征。例如,某些特定的纹理可能在频域中表现出独特的模式,这些模式可用于识别或分类目的。
-
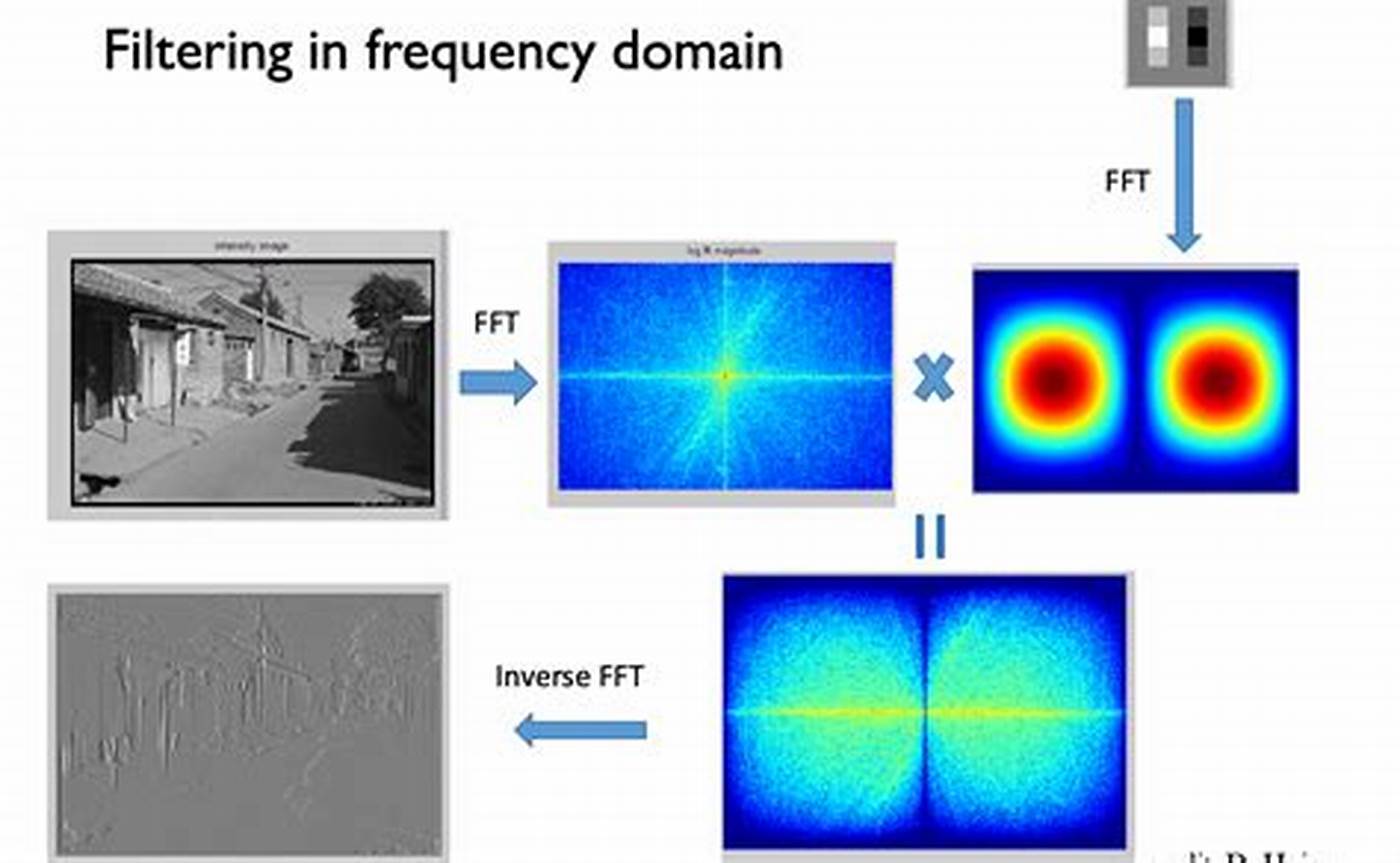
卷积运算:
在空间域中进行卷积操作计算成本较高,尤其是在处理大型核时。而在频域中,卷积操作转化为简单的乘法运算,大大提高了计算效率。这对于执行模糊、锐化等操作非常有用。 -
图像重建与恢复:
对于一些因采集过程中的物理限制而退化的图像(如运动模糊或光学系统的衍射极限),可以利用傅里叶变换技术来尝试恢复原始图像的质量。 -
噪声去除:
利用傅里叶变换可以有效地识别和去除周期性噪声。由于这类噪声通常集中在特定的频率范围内,因此可以在不严重影响图像其余部分的情况下将其过滤掉。 -
相位相关:
在图像配准(即对齐两张或多张图像)中,傅里叶变换可以帮助找到图像之间的位移。通过对两幅图像进行傅里叶变换,并使用它们的相位信息,可以计算出图像间的相对平移量。
总之,傅里叶变换提供了一种强大的工具,使得我们能够从不同的角度理解和处理图像,特别是在涉及频率分析和滤波的任务中显示出其独特的优势。






