欲穷千里目,更上一层楼。

前言
这是我自己学习C++的第十六篇博客总结。后期我会继续把C++学习笔记开源至博客上。
上一期笔记是关于C++的AVL树知识,没看的同学可以过去看看:
【C++】AVL树-CSDN博客
https://blog.csdn.net/hsy1603914691/article/details/147250482
红黑树
红黑树的概念
1. 红黑树是一种二叉搜索树。在红黑树中,每个节点除了保存键值之外,还增加了一个额外的颜色属性,颜色可以是红色或黑色。
2. 通过对从根节点到叶子节点的每条路径上的节点颜色进行约束,红黑树保证了任意一条路径的长度都不会超过其他路径长度的两倍,因此红黑树是接近平衡的。
红黑树的规则
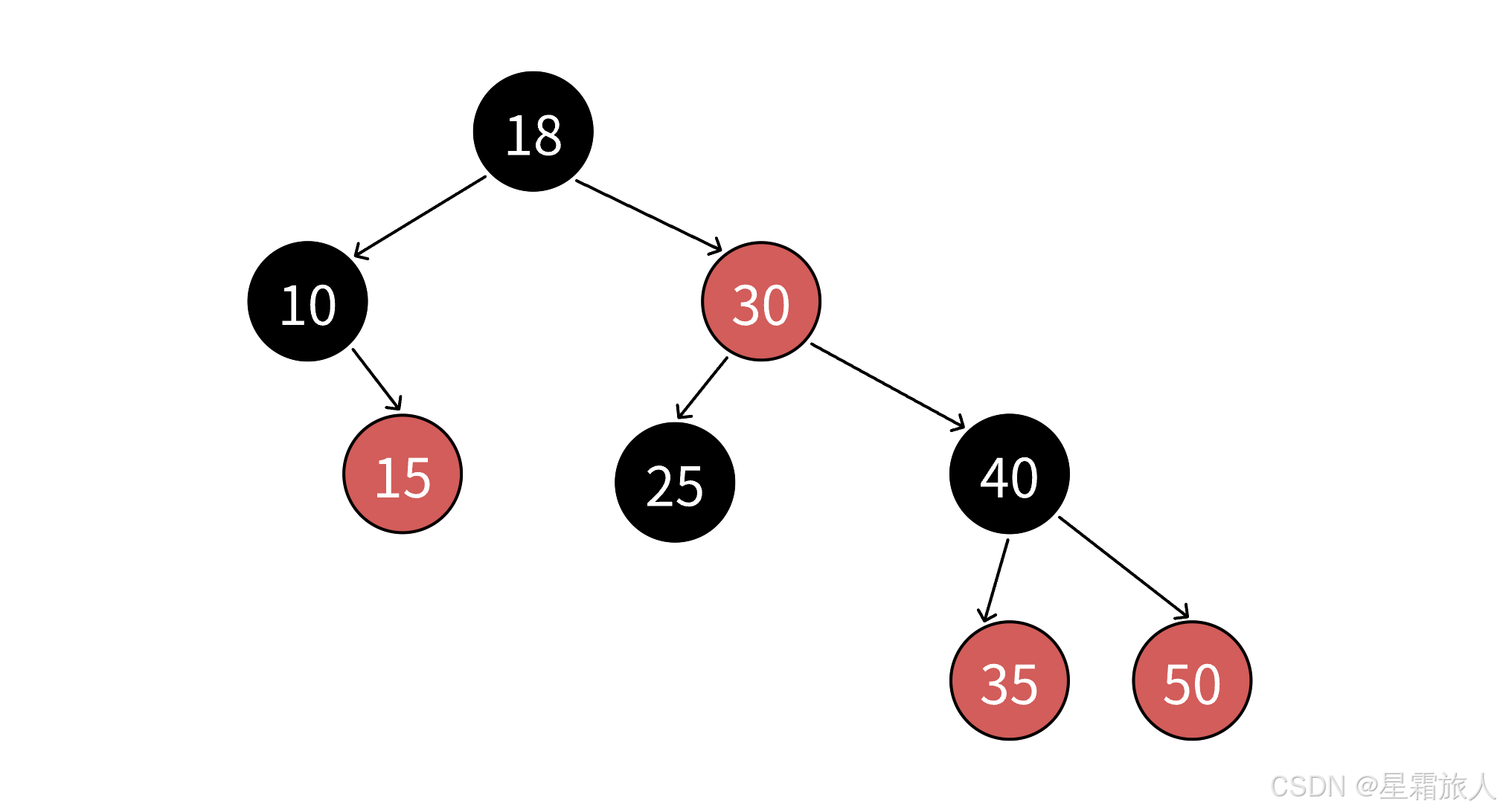
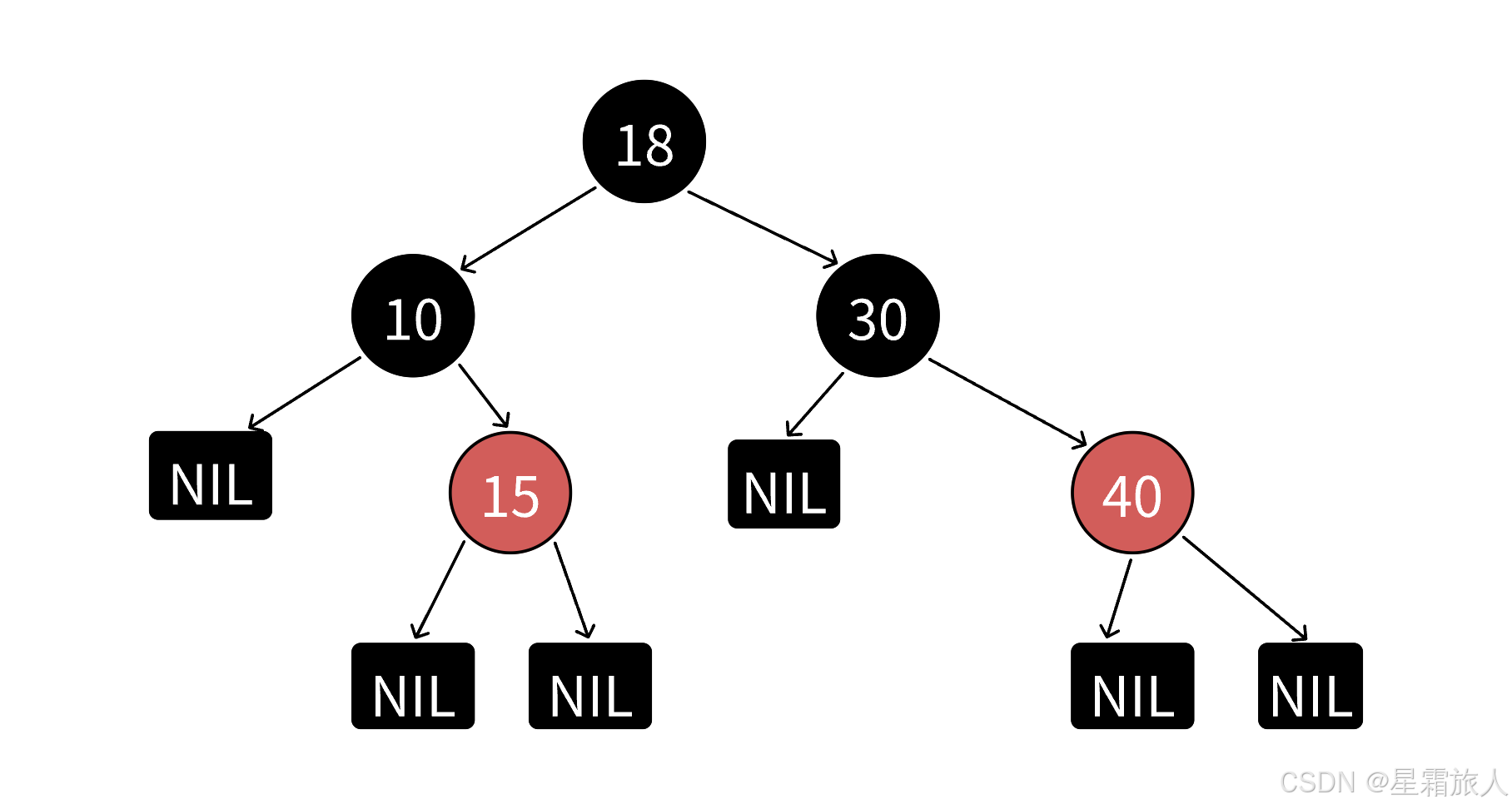
1. 每个结点不是红色就是黑色 。2. 根结点是黑色 。3. 如果一个结点是红色的,则它的两个孩子结点必须是黑色的 。4. 对于任意一个结点,从该结点到其所有NULL结点的简单路径上,均包含相同数量的黑色结点 。
红黑树的效率
1. 红黑树 的查找效率为 O(logN) 。2. AVL树 通过 高度差 直观的控制了平衡; 红黑树 通过 4条规则的颜色约束 ,间接的实现了近似平衡。 它们效率都是同一档次 ,但 是相对而言,插 入相同数量的结点, 红黑树的旋转次数是更少的 。
#include <iostream>
using namespace std;enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{typedef RBTreeNode<K, V> Node;K _key;V _val;Node* _left;Node* _right;Node* _parent;Colour _col;RBTreeNode(const K& key, const V& val): _key(key), _val(val), _col(RED), _left(nullptr), _right(nullptr), _parent(nullptr){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;typedef RBTree<K, V> Tree;
public:RBTree():_root(nullptr){}bool insert(const K& x, const V& y){if (_root == nullptr)//如果插入的节点为根节点{_root = new Node(x, y);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur != nullptr)//找到新节点的插入位置{if (cur->_key < x){parent = cur;cur = cur->_right;}else if (cur->_key > x){parent = cur;cur = cur->_left;}else{return false;//不允许有重复}}cur = new Node(x, y);if (parent->_key < cur->_key)//插入新节点{parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent&&parent->_col==RED)//父节点为红色{Node* grandfather = parent->_parent;if (grandfather->_left == parent)//父节点在左侧{Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//叔叔节点存在,且为红色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else//叔叔节点不存在;叔叔节点存在,且为黑色{if (cur == parent->_left)//插入节点在父节点左侧{Rotate_Right(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else//插入节点在父节点右侧{Rotate_Left(parent);Rotate_Right(grandfather);grandfather->_col = RED;cur->_col = BLACK;}break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;}else{if (cur == parent->_right){Rotate_Left(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{Rotate_Right(parent);Rotate_Left(grandfather);grandfather->_col = RED;cur->_col = BLACK;}break;}}}return true;}void InOrder(){_InOrder(_root);}Node* Find(const K& x){Node* cur = _root;while (cur != nullptr){if (cur->_key < x){cur = cur->_right;}else if (cur->_key > x){cur = cur->_left;}else{return cur;}}return nullptr;}void InOrder(){_InOrder(_root);cout << endl;}bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){// 前序遍历走到空时,意味着一条路径走完了if (refNum != blackNum){cout << "存在黑色结点的数量不相等的路径" << endl;return false;}return true;}// 检查孩子不太方便,因为孩子有两个,且不一定存在,反过来检查父亲就方便多了if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色结点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;// 参考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}
private:Node* _root;void _InOrder(Node* root){if (root == nullptr){return;}else{_InOrder(root->_left);cout << root->_key << " " << root->_val << endl;_InOrder(root->_right);}}void Rotate_Right(Node* parent){Node* ppNode = parent->_parent;Node* sub_left = parent->_left;Node* subl_right = sub_left->_right;sub_left->_right = parent;parent->_parent = sub_left;parent->_left = subl_right;if (subl_right){subl_right->_parent = parent;}if (ppNode == nullptr){_root = sub_left;sub_left->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = sub_left;}else{ppNode->_right = sub_left;}}}void Rotate_Left(Node* parent){Node* ppNode = parent->_parent;Node* sub_right = parent->_right;Node* subr_left = sub_right->_left;sub_right->_left = parent;parent->_parent = sub_right;parent->_right = subr_left;if (subr_left){subr_left->_parent = parent;}if (ppNode == nullptr){_root = sub_right;sub_right->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = sub_right;}else{ppNode->_right = sub_right;}}}};
int main()
{RBTree<int, int> rbt;rbt.insert(999, 1);rbt.insert(998, 2);rbt.insert(997, 3);rbt.insert(996, 4);rbt.insert(995, 5);rbt.insert(994, 6);rbt.insert(993, 7);rbt.insert(992, 8);rbt.insert(991, 9);rbt.insert(990, 10);rbt.InOrder();return 0;
}在这里获取最长路径和最短路径,检查最长路径不超过最短路径的2倍是不可行的,因为即使满足这个条件,红黑树也可能颜色不满足规则。当前看起来没有问题,但在后续继续插入节点时可能会出现问题。因此,我们应当检查四点规则,满足这四点规则能够保证最长路径不超过最短路径的2倍。1. 规则1:枚举颜色类型,这样实现可以保证颜色不是黑色就是红色。
2. 规则2:直接检查根节点即可。
3. 规则3:通过前序遍历检查,当遇到红色节点时查找孩子节点不太方便,因为孩子节点有两个,且不一定存在。相反,检查父节点的颜色更为方便。
4. 规则4:在前序遍历中,使用形参记录从根节点到当前节点的黑色节点数量。遍历过程中,遇到黑色节点就增加黑色节点数量,遍历到空节点即可计算出一条路径的黑色节点数量。将任意一条路径的黑色节点数量作为参考值,依次比较即可。



)



