数据结构【二叉树——堆】

1.二叉树的概念与性质

二叉树的概念

二叉树也是树的一种，但是他最多有两个子树（度最大为2），一颗二叉树是结点的有限集合，
这个集合要么为空，要么就是由一个根节点加上被称为左子树和右子树的二叉树组成。

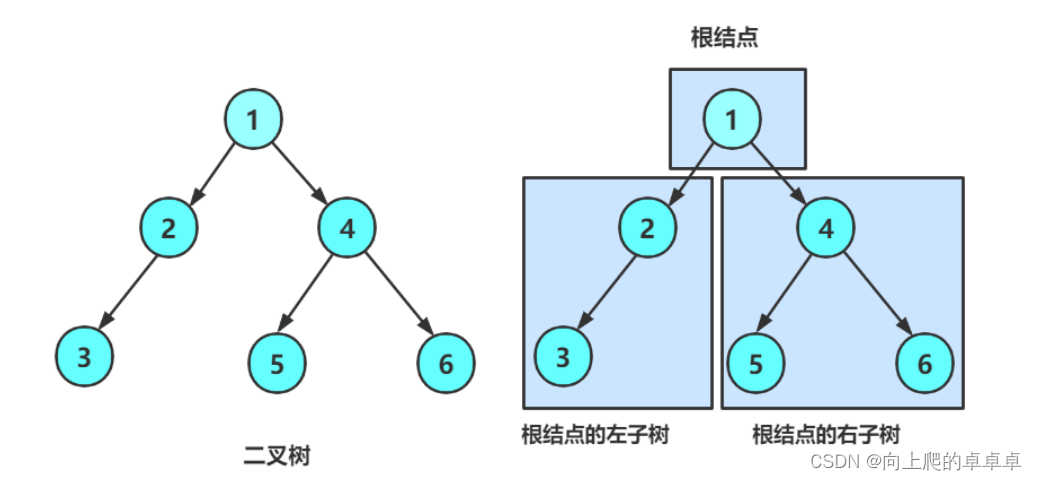
从上图可以看出：

• 二叉树不存在度大于二的结点
• 二叉树的子树有左右之分，顺序不能颠倒，因此二叉树是有序树

注：下图都是二叉树

特殊的二叉树

• 满二叉树：当每一层的结点数都是最大的时候，这颗二叉树就是一颗满二叉树；假设这块树的高度为 h，那么这颗树最后一层的结点数量就为2^h-1个，结点总数量为2^h -1
• 完全二叉树：他的前 h-1层都是满的，最后一层不一定满（1~2^h-1个）；此外最后一层的结点必须是从左到右连续的。需要注意的是满二叉树是一种特殊的完全二叉树。
  

2.二叉树的性质

以下性质的根节点的层数都为1

1. 一颗非空二叉树在第i层最多有2^i-1 个结点。
2. 假设一颗二叉树的深度为h，那么这颗二叉树的最大结点数为2^h-1。
3. 对任意一颗二叉树，如果度为0的叶子结点的个数为$n_0$，度为2的分支结点的个数为$n_2$，就会有$n_0=n_2+1$

假设二叉树有N个结点
那么从总结点的角度考虑：$N=n_0+n_1+n_2$($n_1$代表度为1的分支结点)

---

从边的角度，N个结点的任意二叉树，总共有N-1条边
因为二叉树的每个结点都是父节点，而根结点没有父节点，每个结点与父节点之间有联系（也就是边），所以N个结点的二叉树一共有N-1条边

---

因为度为0的结点没有孩子，所以度为0的结点不产生边；度为1的结点只有一个孩子，所以每个度为1的结点产生一条边；度为2的结点有两个孩子，所以每个度为2的结点产生两条边，所以总边数为：$n_1+n_2\ast 2$
由于N个结点的任意二叉树，总共有N-1条边
所以从边的角度考虑：$N-1=n_1+n_2\ast 2$

---

结合总结点与边的两个公式得出$n_0+n_1+n_2=n_1+n_2\ast 2+1$
即为$n_0=n_2+1$

4.具有n个结点的满二叉树，那么他的深度为$h=lo{g}_2(n+1)$

总结点为$n=2^h-1$
$n+1=2^h$
$lo{g}_2(n+1)=h$ -> $h=lo{g}_2(n+1)$

5.对于具有n个节点的完全二叉树，如果是按照从上到下、从左到右的数组顺序对所有结点从0开始进行编号，则序号为i 的结点有：

1. i>0，i位置结点的父节点序号为:(i - 1) / 2；i = 0，则 i 为根结点，无父节点
2. 若2 * i + 1 < n，则左孩子序号为：2 * i + 1，若2 * i + 1 >= n，则 i 结点无左孩子
3. 若2 * i + 2 < n，则右孩子序号为：2 * i + 2，若2 * i + 2 >= n，则 i 结点无右孩子

3.二叉树的存储结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链表结构。

顺序结构

顺序结构存储就是用数组来存储，但只适合表示完全二叉树，因为完全二叉树能填满数组，非完全二叉树总是会有一块空间不存放值，就会造成空间浪费。二叉树顺序存储在物理结构上是一个数组，在逻辑结构上是一颗二叉树。

链式结构

链式结构存储是指用链表来表示一颗二叉树，即用链表来表示逻辑关系，一个二叉树结点分为数据域和左右指针域，左右指针分别指向左右孩子所在的结点的地址。
链式结构分为二叉链和三叉链，三叉链是多一个指向父节点的指针。

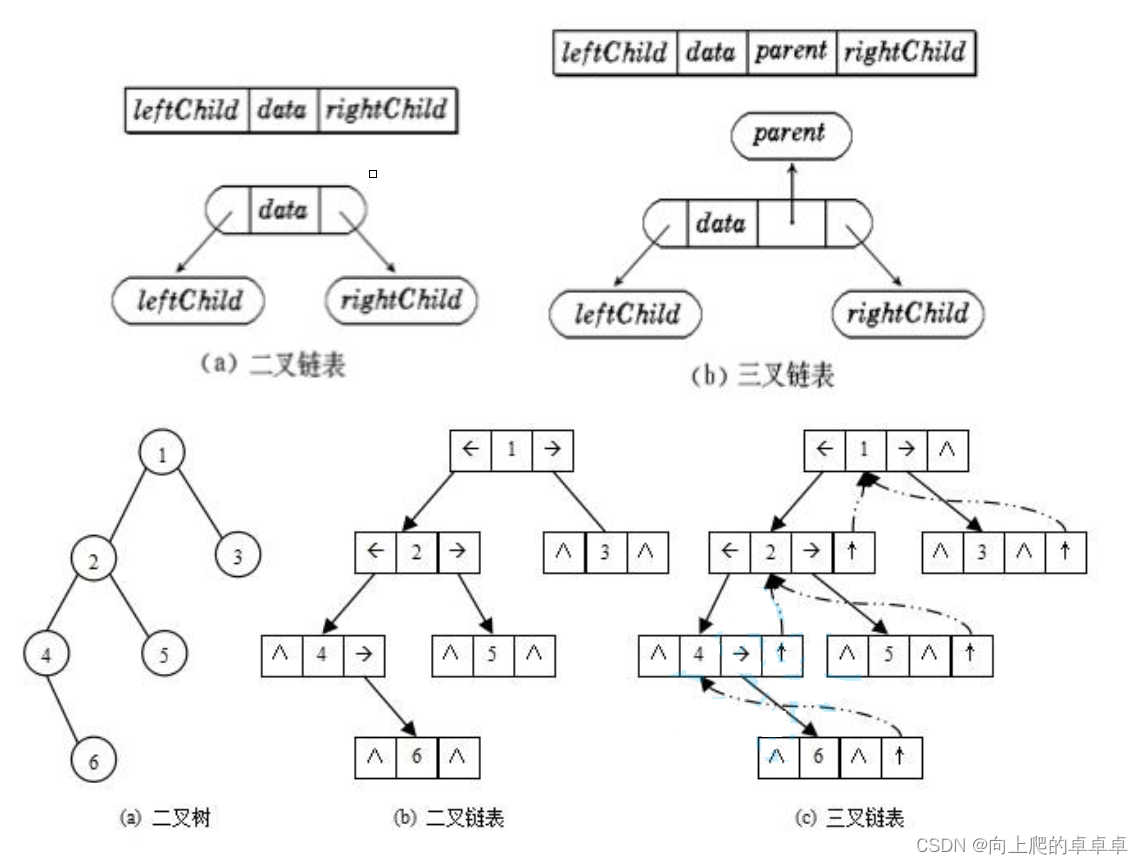
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
struct BinTreeNode* left; // 指向当前结点左孩子
struct BinTreeNode* right; // 指向当前结点右孩子
BTDataType data; // 当前结点值域
}
// 三叉链
struct BinaryTreeNode
{
struct BinTreeNode* parent; // 指向当前结点的双亲
struct BinTreeNode* left; // 指向当前结点左孩子
struct BinTreeNode* right; // 指向当前结点右孩子
BTDataType data; // 当前结点值域
}；

4.堆

因为普通的二叉树不适合顺序结构，因为可能会造成大量的空间浪费。而完全二叉树更加适合顺序结构存储。在现实使用的时候，我们通常把堆（一种二叉树）使用顺序结构来存储，要注意这里的堆和操作系统的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段（栈和操作系统的栈同理）。

堆的概念

1. 堆是一个完全二叉树
2. 堆分大小堆

大堆：根结点的元素最大，父结点大于子节点
小堆：根结点的元素最小，父结点小于子结点

注意：堆并不是有序的，堆仅仅约束了父亲与孩子之间的大小关系，并没有约束兄弟之间的关系

堆接口的实现（默认为大堆）

因为是用数组来实现，所以大体和栈、顺序表的实现是一样的，所以我们的重心会放在插入和删除上

堆的结构

typedef int HPDataType;typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;

堆的初始化

// 堆的初始化
void HeapInit(Heap* hp)
{assert(hp);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}

堆的销毁

// 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}

栈的插入

插入有三种情况

1. 插入的数比父亲小
2. 插入的数比父亲大但是比祖宗大
3. 插入的数比所有值都大

第一种情况堆就不需要调整，其他两种情况就需要向上调整。
向上调整算法就是当我插入的数据比父亲大，就交换数据，直到成为了根或者是父亲比孩子大，这样一直循环下去就能每次把最大的数往上抬。

//交换函数
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//向上调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0)//当孩子成了根，就跳出循环{if (a[parent] < a[child])//当父亲小于孩子{Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else//父亲大于孩子，不用再调整了{break;}}
}

插入代码：

//交换函数
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//向上调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[parent] < a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else{break;}}
}// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->_size == hp->_capacity){int NewCapacity = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;HPDataType* tmp = (HPDataType*)realloc(hp->_a, NewCapacity*sizeof(HPDataType));if (tmp == 0){perror("realloc fail");return;}hp->_capacity = NewCapacity;hp->_a = tmp;}hp->_a[hp->_size++] = x;AdjustUp(hp->_a, hp->_size - 1);
}

堆的删除

我们删除堆底的数据是没有意义，删除堆都是删除对顶的数据（堆顶要么最大要么最小），将堆顶数据与最后一个数据进行交换，再进行向下调整算法。
向下调整算法我们是从父亲结点开始往下调整，看左右孩子哪个更大，就与哪个孩子交换，直到没有成为叶子结点或者比孩子都大，这样我们删除最大的数据之后，就可以把次大的数据冒到堆顶。

//交换函数
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//向下调整算法
void AdjusDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//假设法//先假设左孩子大，当右孩子大于左孩子的时候，child++变更成右孩子if (child+1 < n && a[child] < a[child + 1]){child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}// 堆的删除
void HeapPop(Heap* hp)
{assert(hp);//先删除Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;//再调整AdjusDown(hp->_a, hp->_size, 0);
}

取堆顶数据

// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->_a[0];
}

堆的元素个数

// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}

堆的判空

// 堆的判空
bool HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;
}

完整代码

Heap.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef int HPDataType;typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;
// 堆的初始化
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);

Heap.c(实现部分)

#include"Heap.h"//交换函数
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}// 堆的初始化
void HeapInit(Heap* hp)
{assert(hp);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}// 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}//向上调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[parent] < a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else{break;}}
}// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->_size == hp->_capacity){int NewCapacity = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;HPDataType* tmp = (HPDataType*)realloc(hp->_a, NewCapacity*sizeof(HPDataType));if (tmp == 0){perror("realloc fail");return;}hp->_capacity = NewCapacity;hp->_a = tmp;}hp->_a[hp->_size++] = x;AdjustUp(hp->_a, hp->_size - 1);
}//向下调整算法
void AdjusDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child+1 < n && a[child] < a[child + 1]){child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}// 堆的删除
void HeapPop(Heap* hp)
{assert(hp);Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;AdjusDown(hp->_a, hp->_size, 0);
}// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->_a[0];
}// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}// 堆的判空
bool HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;
}

test.c(测试部分)

#include"Heap.h"void TestHeap()
{int a[] = { 5,6,7,9,1,3,4,2,8,10 };Heap hp;HeapInit(&hp);for (int i = 0; i < sizeof(a)/sizeof(int); i++){HeapPush(&hp, a[i]);}while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}HeapDestory(&hp);}int main()
{TestHeap();return 0;
}

结语

最后感谢您能阅读完此片文章，如果有任何建议或纠正欢迎在评论区留言，也可以前往我的主页看更多好文哦(点击此处跳转到主页)。
如果您认为这篇文章对您有所收获，点一个小小的赞就是我创作的巨大动力，谢谢！！！