
rabbitmq 6种模式

sql连接
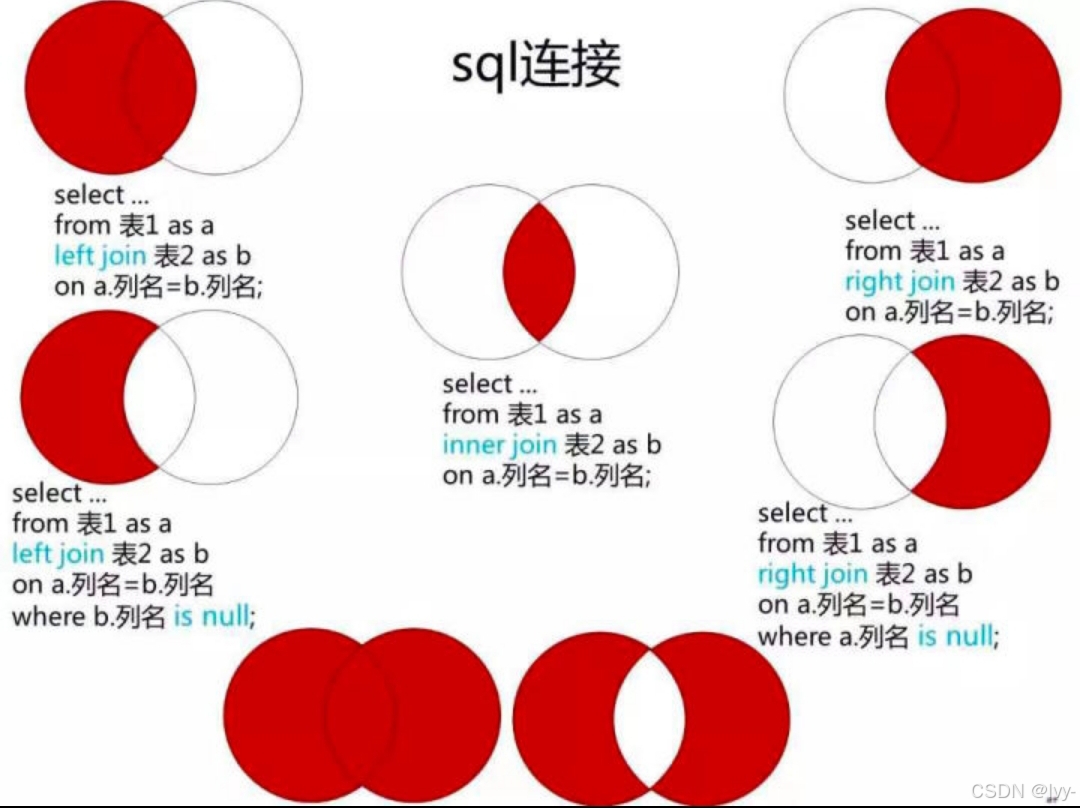
select p.FirstName,p.LastName,a.City,a.State
from
person p left join address a
on
p.personid=a.personid
2的幂再和,二进制取模相加==n

1. 分解n为2的幂次:
- 利用二进制特性,n的每一位1对应一个唯一的2的幂次(如n=10=8+2=2³+2¹,对应powers=[2,8])。
- 通过不断对n取余和整除2,提取每一位二进制位,将对应的幂次存入 powers 数组。
2. 处理查询:
- 每个查询给出一个区间 [l, r] ,表示求 powers[l] * powers[l+1] * ... * powers[r] 的结果。
- 由于结果可能很大,每次乘法后都对 1e9+7 取模(利用模运算性质防止溢出)。
3. 注意点:
- 使用 long long 存储中间结果,避免整数溢出。
- powers 数组的下标直接对应查询中的区间端点(如查询 [0,2] 表示取前3个幂次相乘)。
示例理解:
- - 若 n=15 (二进制 1111 ),则 powers = [1,2,4,8] 。
- - 查询 [0,2] 对应计算 1*2*4=8 ,查询 [1,3] 对应 2*4*8=64 。
class Solution {
public:
vector<int> productQueries(int n, vector<vector<int>>& queries) {
// 造powers数组
vector<int> powers;
// 由n变到1powers数组
for(int i=0,i1=1,j=0;n>0;)
{
i=n%2;
if(i==1) {powers.push_back(i1);j++;}
n/=2;i1*=2;
}
// return powers;
// 造answers数组
vector<int> answers;
for(int i=0; i<queries.size(); i++)
{
long long ans=1;
int c=1e7;
for(int k=queries[i][0]; k<=queries[i][1]; k++)
{ans=((ans%c)*(powers[k]%c))%c;}
//求区间乘积
//利用了(a*b)%c=((a%c)*(b%c))%c 拆分取模,防止溢出
answers.push_back(ans);
}
return answers;
}
};
爬楼梯
class Solution {
public:
int climbStairs(int n)
{
if(n<3) return n;
vector<int> dp(n+1);
dp[1]=1,dp[2]=2;
for(int i=3;i<=n;i++)
{
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
};
接雨水

这段代码用「栈」来计算接雨水的量,核心逻辑是:
从左到右遍历每个柱子,用栈记录「可能成为左边边界」的柱子下标。
当遇到更高的柱子(右边界)时,计算两者之间的「凹槽储水量」:
1. 弹出栈顶(中间柱子),若栈空则无法形成凹槽,跳过。
2. 确定左右边界:新栈顶是左边界,当前下标是右边界。
3. 计算高度差:左右边界的最小值 - 中间柱子高度,得到储水高度。
4. 计算宽度:右边界下标 - 左边界下标 - 1,乘高度得到水量,累加到结果。
举例:柱子高度为 [0,1,0,2,1,0,1,3,2,1,2,1] ,
遍历到 i=3 (高度2)时,栈中是 [0,1] (高度0,1),
弹出1(高度1),左边界是0(高度0),右边界是3(高度2),
储水高度 = min(0,2) - 1 = -1?不,这里实际是 min(左边界高度, 右边界高度) - 中间高度,
左边界高度是 height[0]=0 ,右边界是 height[3]=2 ,中间是 height[1]=1 ,
所以储水高度是 0-1?不对! 哦这里发现描述有误,正确逻辑是:只有左右边界都高于中间柱子时才有储水,
所以当右边界高度 > 中间柱子时,左边界必须存在且高度 > 中间柱子,
此时储水高度 = min(左边界高度, 右边界高度) - 中间高度,
宽度是右边界下标 - 左边界下标 - 1。
代码通过栈动态维护左右边界,逐个计算每个凹槽的水量,最终总和就是答案。
int trap(vector<int>& height)
{
int ans = 0;
stack<int> st;
for (int i = 0; i < height.size(); i++)
{
while (!st.empty() && height[st.top()] < height[i])
{
int cur = st.top();
st.pop();
if (st.empty()) break;
int l = st.top();
int r = i;
int h = min(height[r], height[l]) - height[cur];
ans += (r - l - 1) * h;
}
st.push(i);
}
return ans;
}
双指针
class Solution {
public:
int trap(vector<int>& height) {
int ans = 0, left = 0, right = height.size() - 1, pre_max = 0, suf_max = 0;
while (left < right) {
pre_max = max(pre_max, height[left]);
suf_max = max(suf_max, height[right]);
ans += pre_max < suf_max ? pre_max - height[left++] : suf_max - height[right--];
}
return ans;
}
};
dfs超时优化

注意到 十的九次方
原代码,超时
class Solution {
public:
int n=0;
vector<int> ans;
int findKthNumber(int n, int k)
{
this->n=n;
for(int i=1;i<10;i++)
{
dfs(i);
}
return ans[k-1];
}
void dfs(int num)
{
if(num>n)
{
return;
}
ans.push_back(num);
for(int i=0;i<10;i++)
{
dfs(num*10+i);
}
}
};
数学优化
class Solution {
public:
long getCount(long prefix, long n) {
long cur = prefix;
long next = cur + 1;
long count = 0;
while(cur <= n) {
count += min(n+1, next) - cur;
cur *= 10;
next *= 10;
}
return count;
}
int findKthNumber(int n, int k) {
long p = 1;
long prefix = 1;
while(p < k) {
long count = getCount(prefix, n);
if (p + count > k) {
/// 说明第k个数,在这个前缀范围里面
prefix *= 10;
p++;
} else if (p+count <= k) {
/// 说明第k个数,不在这个前缀范围里面,前缀需要扩大+1
prefix++;
p += count;
}
}
return static_cast<int>(prefix);
}
};
优化思路:
1. 字典序规则:
像查字典一样,先比首位,再比第二位。例如:
- - 1开头的数(1,10,11,12…)比2开头的数(2,20,21…)更小。
2. 关键函数 getCount :
计算以 prefix (如1、10)开头的数字有多少个≤n。
- - 比如 prefix=1 ,n=20时,包含1、10-19、20(共1+10+1=12个)。
- - 计算方式:逐层扩展(1→10→100),每次算当前层有多少个数在n以内。
3.理解
- p++ 是深入子节点找下一个数,
- p += count 是跳过当前前缀,去下一个前缀找。
十叉树
把数字看作树,用子树大小判断第k个数在左子树还是右兄弟:
- - 子树够大:钻进左子树( node*=10 )。
- - 子树不够大:跳过左子树,去右兄弟( node++ )。
通过这种方式,每次跳跃式减少k的范围,效率极高(对数级时间复杂度)。
class Solution {
public:
int findKthNumber(int n, int k) {
// 逐层统计 node 子树大小
auto count_subtree_size = [&](int node) -> int {
// 子树大小不会超过 n,所以 size 用 int 类型
// 但计算过程中的 left 和 right 会超过 int,所以用 long long 类型
int size = 0;
long long left = node, right = node + 1;
while (left <= n) {
// 这一层的最小值是 left,最大值是 min(right, n + 1) - 1
size += min(right, n + 1LL) - left;
left *= 10; // 继续,计算下一层
right *= 10;
}
return size;
};
int node = 1;
k--; // 访问节点 node
while (k > 0) {
int size = count_subtree_size(node);
if (size <= k) { // 向右,跳过 node 子树
node++; // 访问 node 右侧兄弟节点
k -= size; // 访问子树中的每个节点,以及新的 node 节点
} else { // 向下,深入 node 子树
node *= 10; // 访问 node 的第一个儿子
k--; // 访问新的 node 节点
}
}
return node;
}
};
线程

❗模拟➕贪心

要么都变成 1,要么都变成 -1,因此先枚举要变成哪个。
剩下的问题就是一个经典的贪心。
由于乘以 -1 两次之后会变回原数,因此每个下标最多选择一次,且下标选择的顺序没有关系。
不妨假设操作是从左到右进行的。
从左到右考虑每个下标,如果当前值不是目标值,由于后续操作只会影响右边的数,再不操作就没机会了,所以此时必须要选择该下标。
按该贪心思路算出最少操作次数即可,复杂度 O(n) 。
思维题:想到传递的目标判断即可
其实也还可以找奇偶的规律,但是还是这种更好
class Solution {
public:
bool canMakeEqual(vector<int>& nums, int K) {
int n = nums.size();
// 所有值都变成 x 的最少操作次数
auto check = [&](int x) {
int cnt = 0;
vector<int> vec = nums;
// 从左到右考虑每个下标,如果不是目标值,必须操作
for (int i = 0; i + 1 < n; i++) if (vec[i] != x) {
vec[i] *= -1;
vec[i + 1] *= -1;
cnt++;
}
return vec[n - 1] == x && cnt <= K;
};
// 枚举最后变成 1 还是 -1
return check(1) || check(-1);
}
};
总结:
1. 枚举目标:结果只有两种可能——全 1 或者全 -1 。所以我们分别试试这两种情况,看哪种能实现(这就是 “枚举” ,把可能的目标全列出来试)。
2. 贪心操作:确定目标(比如要全 1 )后,怎么操作最省次数?
- 规则是 “选一个下标 i , nums[i] 和 nums[i+1] 都变号” 。而且变号两次等于没变(比如 1 变 -1 再变 1 ),所以每个位置最多操作一次,从左到右处理最合理 。
- 举个例子:数字是 [-1, -1, 1] ,目标要全 1 。从左开始看,第一个数是 -1 (不是目标 1 ),必须操作下标 0 ,让 nums[0] 和 nums[1] 变号,变成 [1, 1, 1] ,这样一次就解决。如果不操作当前下标,后面操作不影响前面,就永远变不成目标了,所以 “遇到不一样的,必须当下操作” ,这就是贪心的 “贪”—— 抓住当下机会,保证结果最优。
移动模拟_优化
原代码
class Solution {
public:
int N;
void move(char c, vector<int>& pos, vector<int>& t) {
if (c == 'L') pos[1] -= 1;
if (c == 'R') pos[1] += 1;
if (c == 'U') pos[0] -= 1;
if (c == 'D') pos[0] += 1;
t = pos;
}
bool check(vector<int>& pos) {
if (pos[0] >= 0 && pos[0] < N && pos[1] >= 0 && pos[1] < N) return true;
else return false;
}
vector<int> executeInstructions(int n, vector<int>& startPos, string s) {
vector<int> res(s.size());
N = n;
for (int i = 0; i < s.size(); i ++ ) {
vector<int> tempos(startPos);
int temres = 0;
for (int j = i; j < s.size(); j ++ ) {
vector<int> t(2);
move(s[j], tempos, t);
if (check(t)) temres ++ ,tempos = t;
else break;
}
res[i] = temres;
}
return res;
}
};
优化:
改用迭代器并内联函数的 C++ 代码(主要修改循环和容器操作部分):
class Solution {
public:
int N;
// 内联移动函数(用引用避免拷贝)
inline void move(char c, vector<int>& pos, vector<int>& t) {
switch(c) {
case 'L': pos[1]--; break;
case 'R': pos[1]++; break;
case 'U': pos[0]--; break;
case 'D': pos[0]++;
}
t = pos; // 更新目标位置
}
// 内联边界检查
inline bool check(const vector<int>& pos) {
return pos[0] >= 0 && pos[0] < N && pos[1] >= 0 && pos[1] < N;
}
vector<int> executeInstructions(int n, vector<int>& startPos, string s) {
vector<int> res(s.size());
N = n;
// 使用迭代器遍历字符串
for(auto it_i = s.begin(); it_i != s.end(); ++it_i) {
vector<int> currentPos = startPos;
int count = 0;
// 从当前迭代器位置开始遍历
for(auto it_j = it_i; it_j != s.end(); ++it_j) {
vector<int> tempPos(2);
move(*it_j, currentPos, tempPos); // 传入字符值
if(check(tempPos)) {
count++;
currentPos = tempPos; // 更新当前位置
} else {
break; // 越界则终止
}
}
res[it_i - s.begin()] = count; // 计算索引
}
return res;
}
};
主要改动点:
1. 函数内联:使用 inline 关键字声明 move 和 check 函数(现代编译器可能自动优化,但显式声明更清晰)
2. 迭代器替代索引:
- 外层循环用 s.begin() / end() 迭代器遍历
- 内层循环从当前迭代器位置 it_i 开始
- 通过 it_i - s.begin() 计算结果数组索引
3. 代码优化:
- switch 替代多个 if 提高分支效率
- currentPos 直接修改减少拷贝(原代码中 tempos = t 可直接操作 currentPos )
- const 修饰 check 函数参数避免意外修改
注意:C++ 中容器迭代器在动态扩容时可能失效,但此处 string 是固定长度,迭代器始终有效,无需担心此问题。
内联函数
内联函数是一种用 inline 关键字声明的特殊函数,目的是让编译器在编译时直接把函数代码「嵌入」到调用它的地方,避免普通函数调用的「跳转开销」,提高程序运行速度。
举个简单例子:
假设有个函数计算两数之和:
int add(int a, int b) {
return a + b;
}
普通调用时,程序会「跳转到函数地址执行代码,再跳转回来」。
如果声明为内联函数:
inline int add(int a, int b) {
return a + b;
}
编译时,编译器会把 add(3,5) 直接替换成 3+5 ,就像你直接写在代码里一样,省去了跳转步骤。
关键特点:
1. 编译时替换:不是运行时调用,而是编译阶段直接「展开代码」。
2. 适合简单函数:通常用于代码量少(如几行)、调用频繁的函数(比如循环里的小操作)。
3. 可能被编译器忽略:最终是否内联由编译器决定(太复杂的函数会被拒绝)。
优点 vs 缺点:
- - 优点:减少函数调用开销,提升执行效率。
- - 缺点:如果函数被多次调用,会导致目标代码体积增大(用空间换时间)。
总结:内联函数就像「把常用的小工具直接粘在使用的地方」,省去了拿工具的步骤,但粘太多会占地方。








