






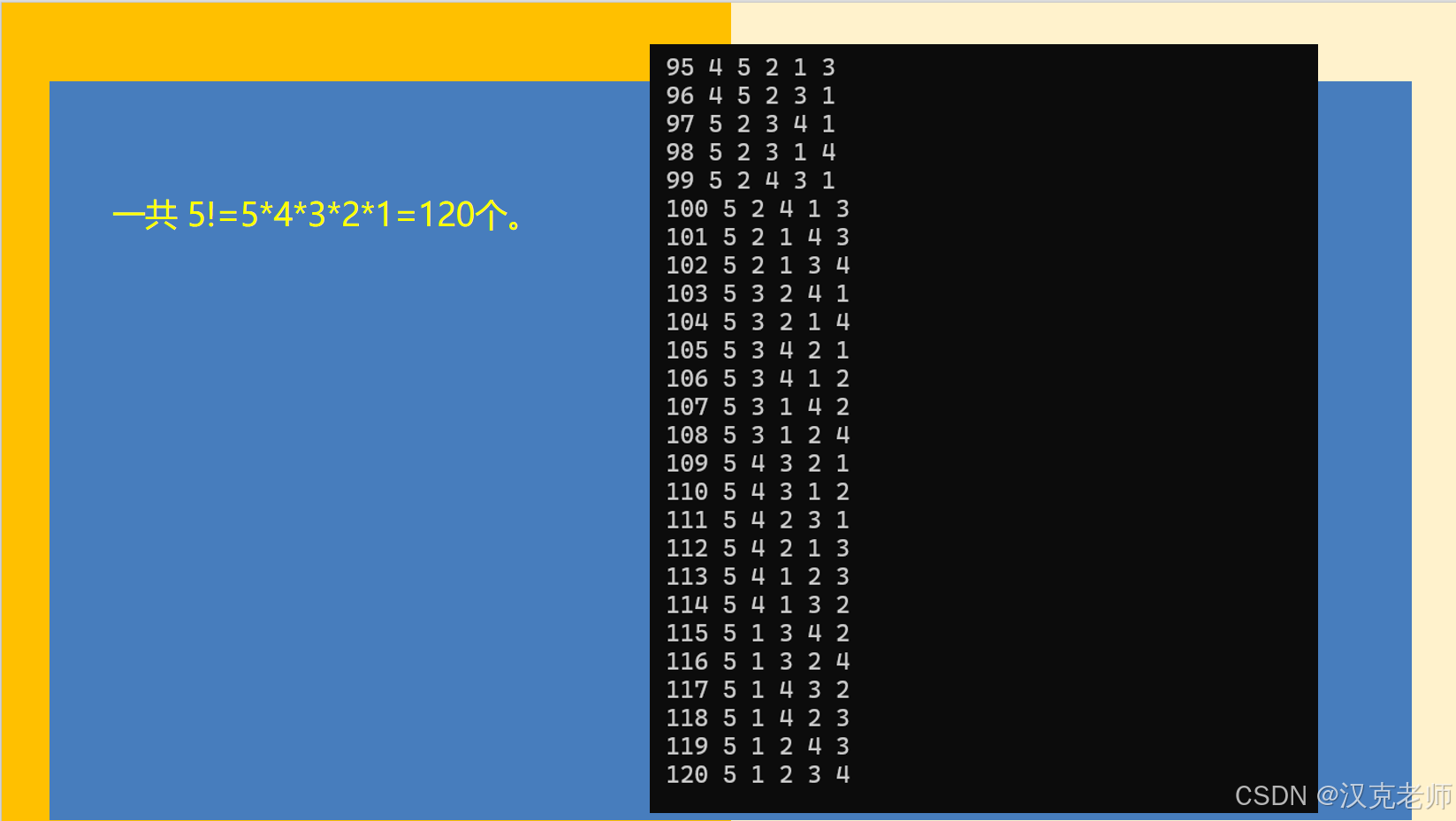





选择题第八题:
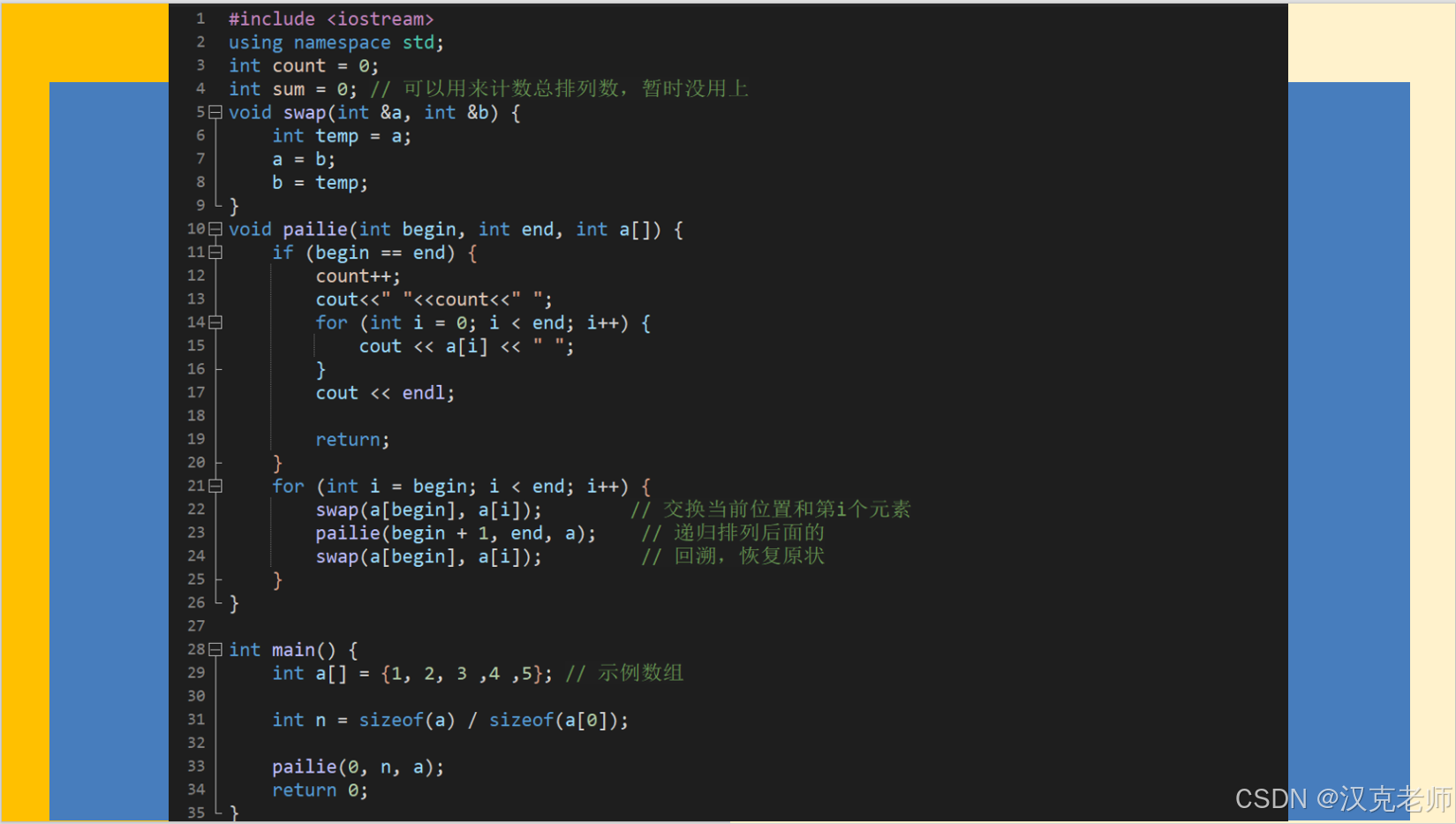
#include <iostream>
using namespace std;
int count = 0;
int sum = 0; // 可以用来计数总排列数,暂时没用上
void swap(int &a, int &b) {int temp = a;a = b;b = temp;
}
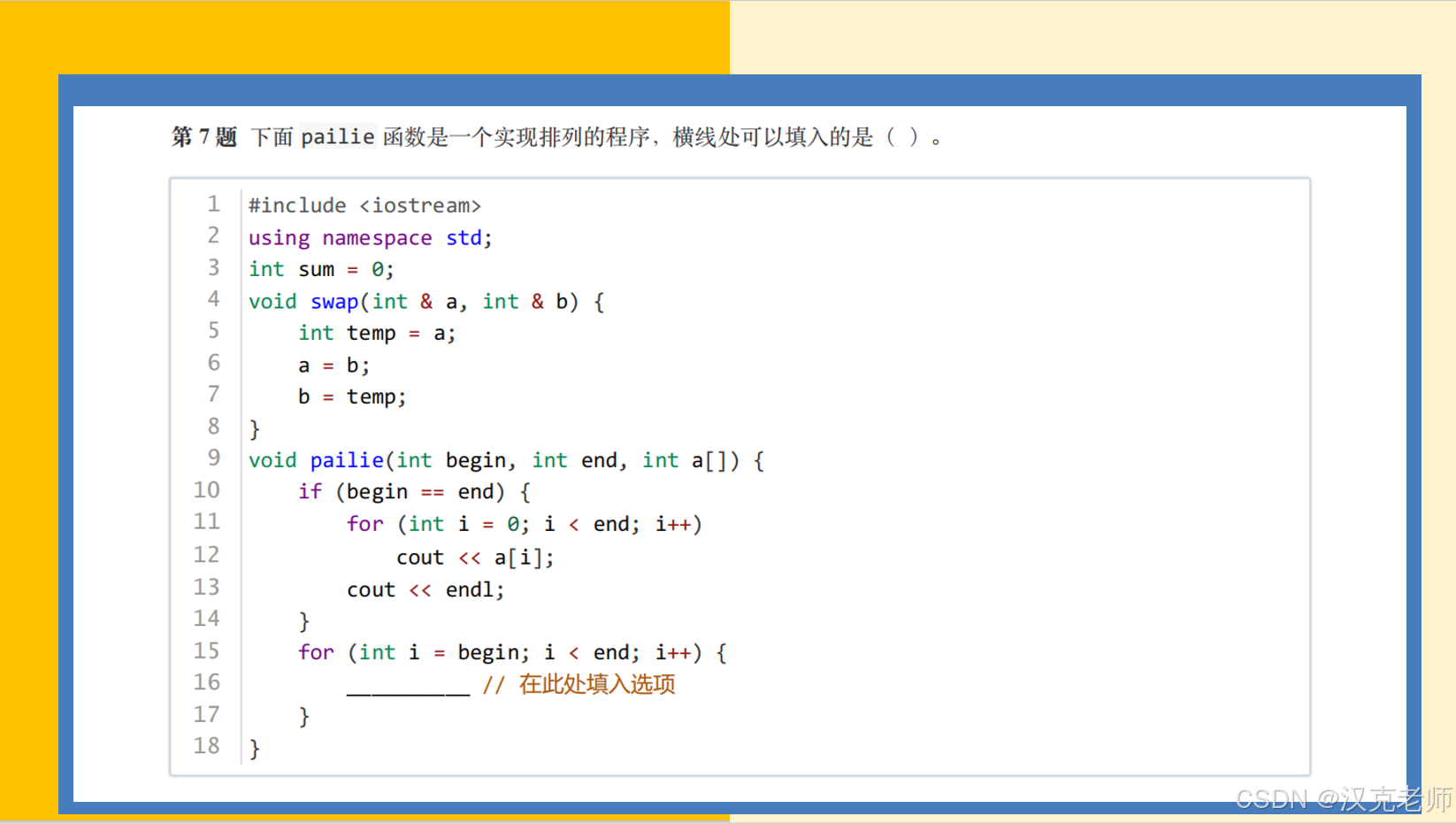
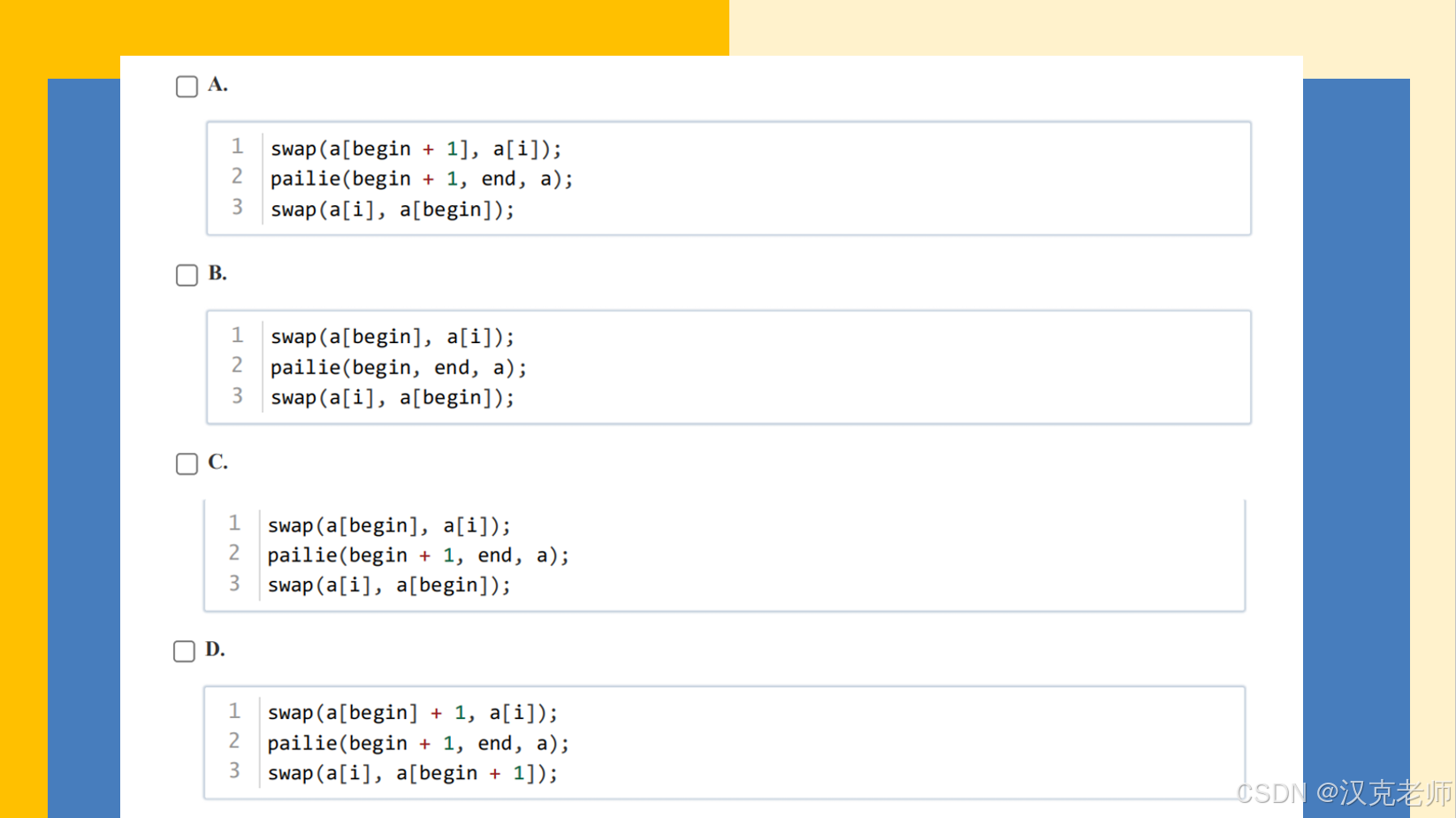
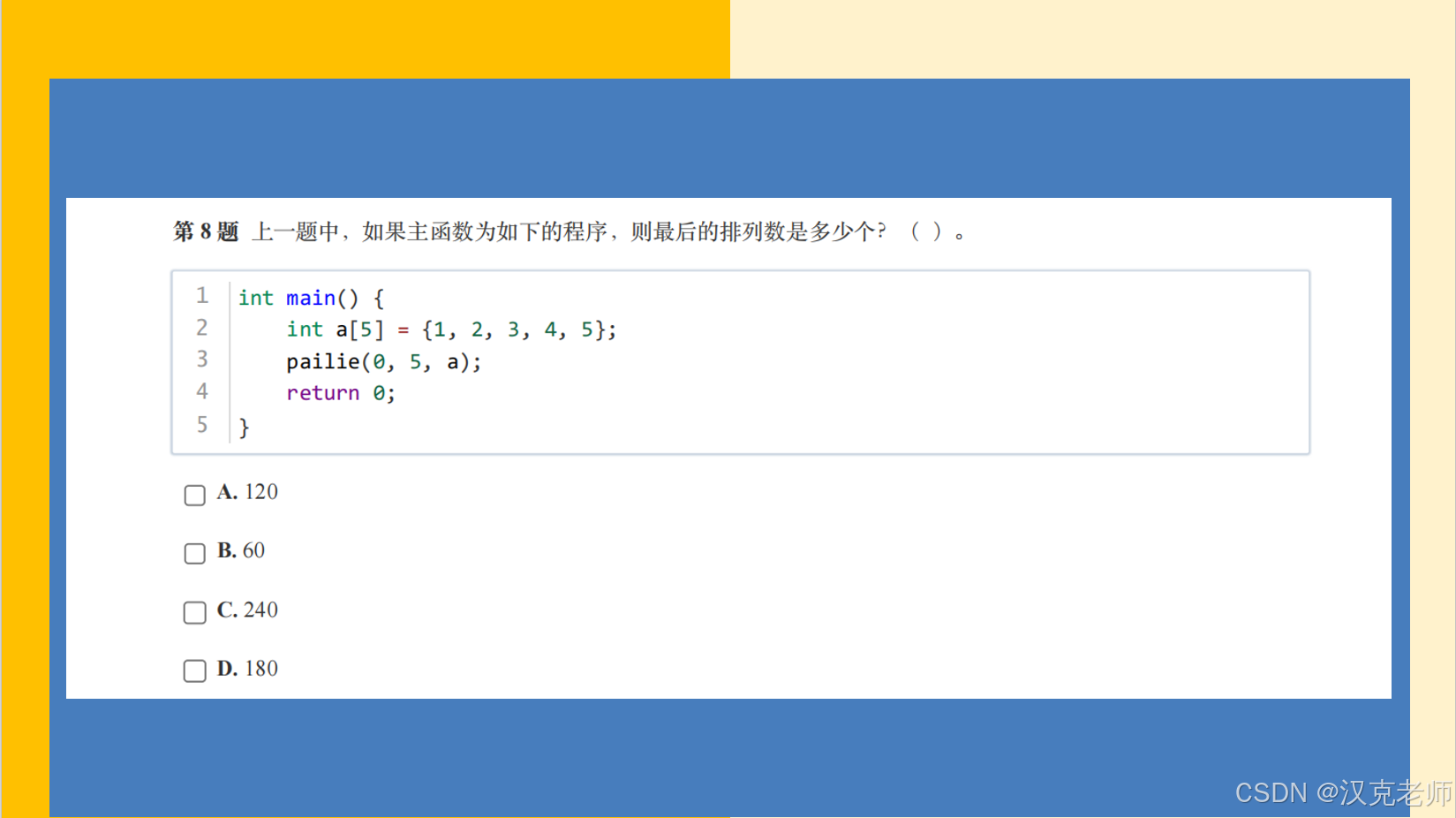
void pailie(int begin, int end, int a[]) {if (begin == end) {count++;cout<<" "<<count<<" ";for (int i = 0; i < end; i++) {cout << a[i] << " ";}cout << endl;return;}for (int i = begin; i < end; i++) {swap(a[begin], a[i]); // 交换当前位置和第i个元素pailie(begin + 1, end, a); // 递归排列后面的swap(a[begin], a[i]); // 回溯,恢复原状}
}int main() {int a[] = {1, 2, 3 ,4 ,5}; // 示例数组int n = sizeof(a) / sizeof(a[0]);pailie(0, n, a);return 0;
}
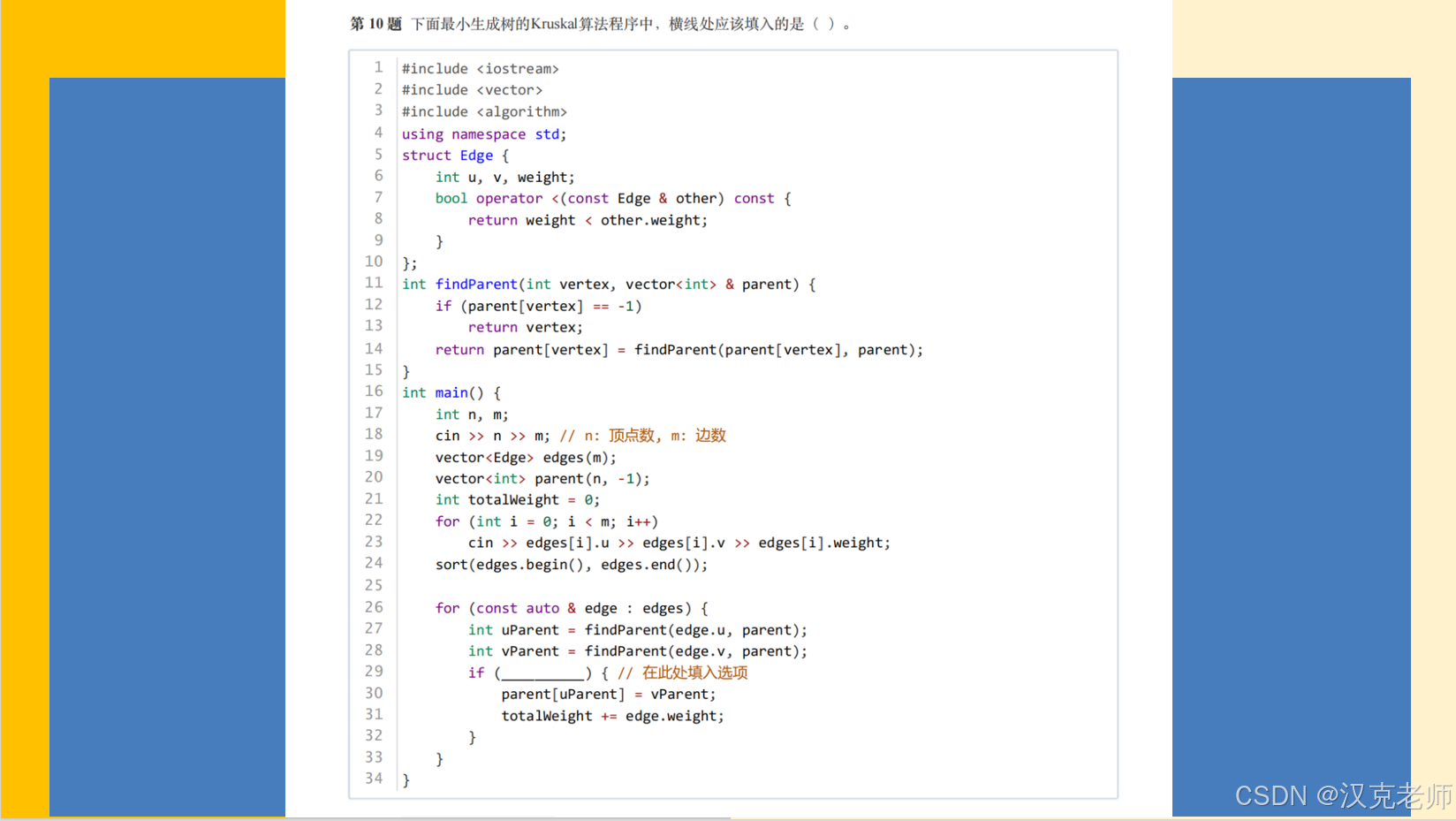
选择题第十题:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;// 定义边的数据结构
struct Edge {int u, v, weight; // u 和 v 是边连接的两个顶点编号,weight 是边的权重// 自定义排序方式:按权重从小到大排列bool operator <(const Edge &other) const {return weight < other.weight;}
};// 并查集查找函数(路径压缩版)
int findParent(int vertex, vector<int> &parent) {if (parent[vertex] == -1) {// 如果当前节点是根节点,直接返回自己return vertex;}// 路径压缩:递归查找父节点,并顺便让当前节点直接指向最终根节点return parent[vertex] = findParent(parent[vertex], parent);
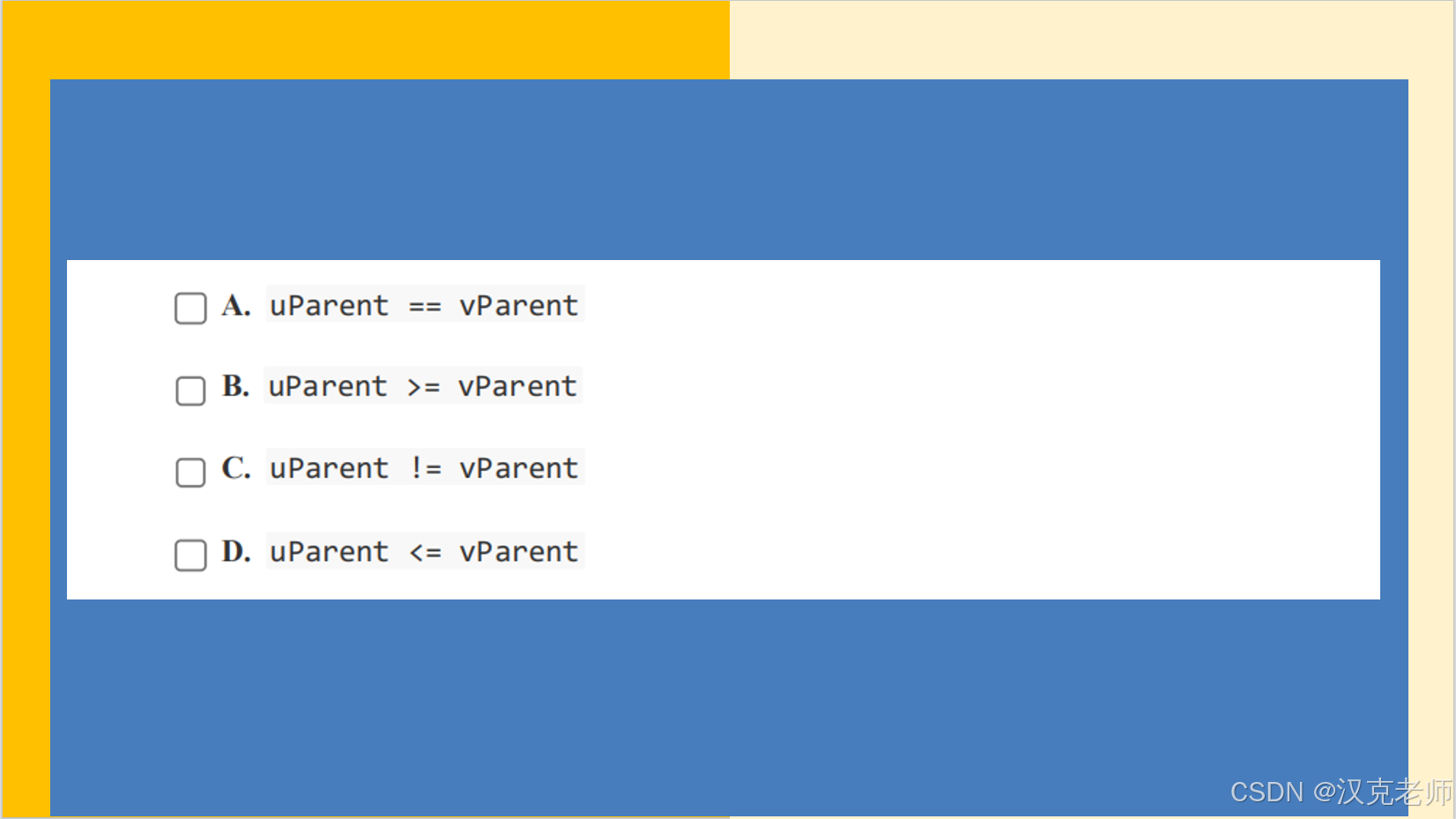
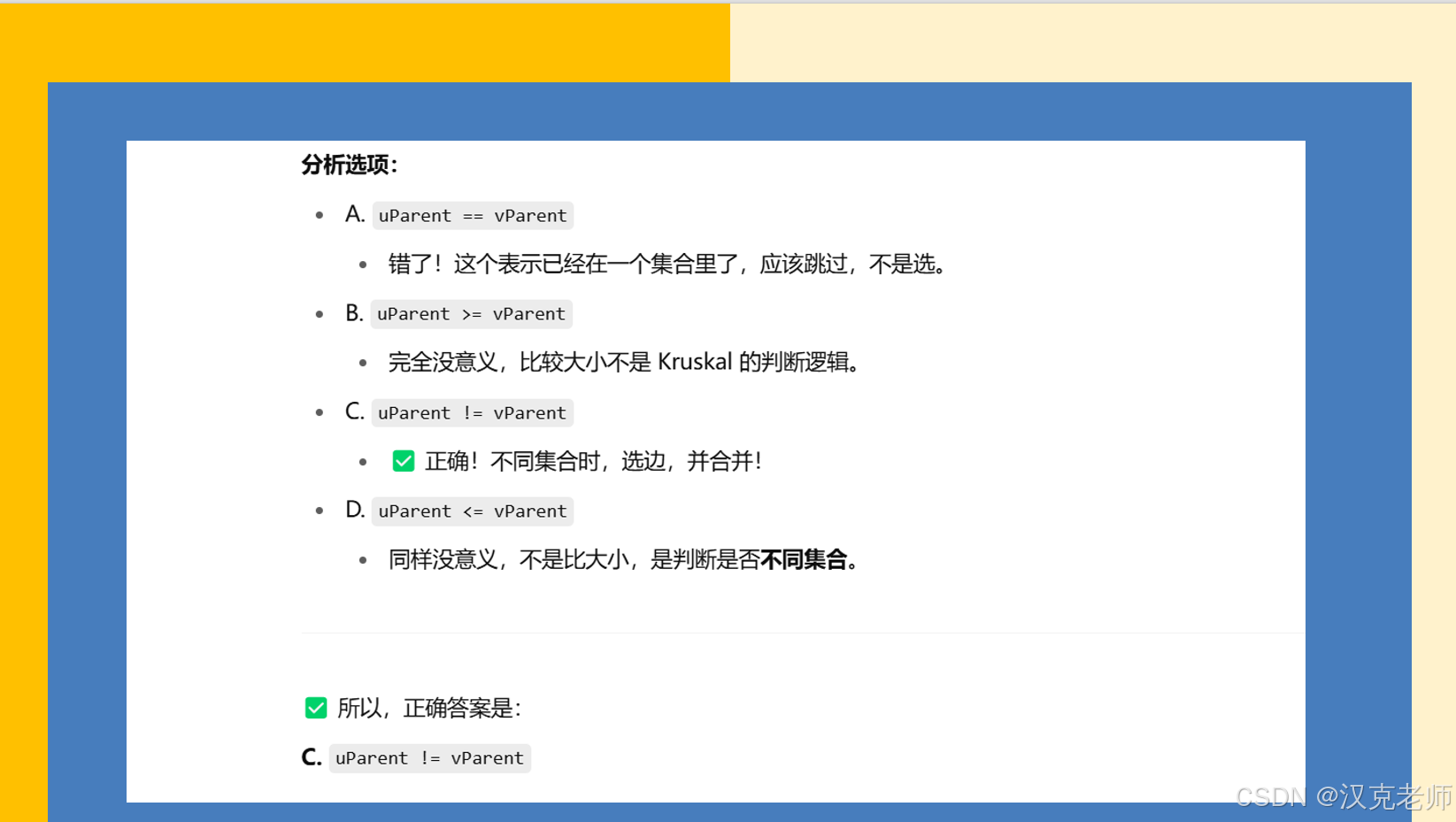
}int main() {int n, m;cin >> n >> m; // n是顶点数,m是边数vector<Edge> edges(m); // 存储所有的边vector<int> parent(n, -1); // 并查集的父节点数组,初始化每个点都是独立的集合int totalWeight = 0; // 记录最小生成树的总权重// 读入所有边的信息for (int i = 0; i < m; i++) {cin >> edges[i].u >> edges[i].v >> edges[i].weight;}// 按边权重从小到大排序sort(edges.begin(), edges.end());// 遍历每条边,尝试加入生成树for (const auto &edge : edges) {int uParent = findParent(edge.u, parent); // 找到u的集合代表int vParent = findParent(edge.v, parent); // 找到v的集合代表if (uParent != vParent) { // 如果u和v属于不同集合(不会形成环)parent[uParent] = vParent; // 合并集合totalWeight += edge.weight; // 把这条边加入生成树,累加权重// (可以在这里记录生成树的边,如果想输出的话)}}// 输出最小生成树的总权重cout << "Total weight of Minimum Spanning Tree: " << totalWeight << endl;return 0;
}选择题第九题:
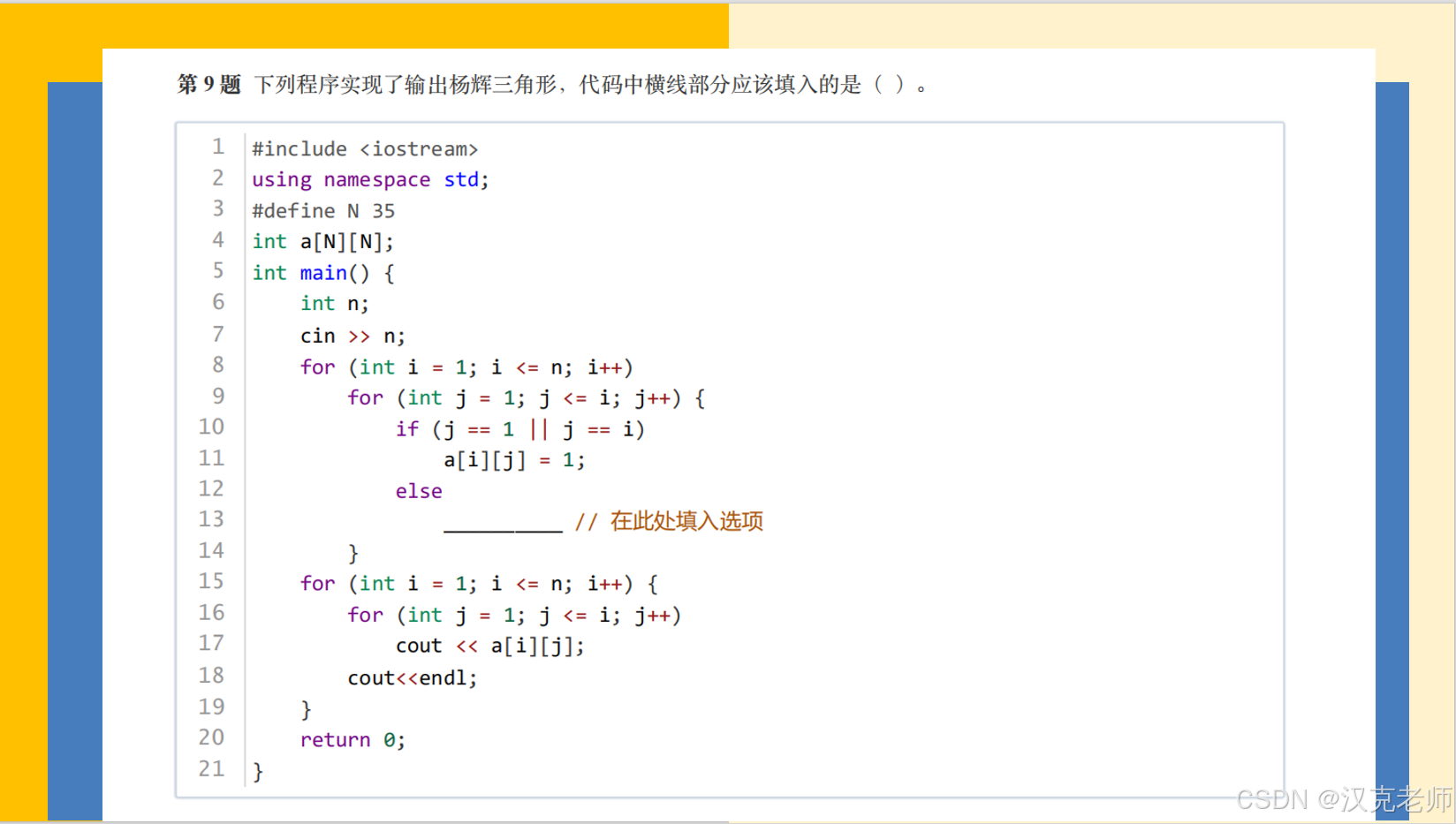
#include <iostream>
using namespace std;#define N 35 // 定义最大的行数,假设最多输出35行int a[N][N]; // 二维数组a用来存储杨辉三角的数值int main() {int n;cin >> n; // 读入需要打印的杨辉三角的行数// 填充杨辉三角的数组for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) { // 每行有i个元素if (j == 1 || j == i) { // 第一列和最后一列的元素是1a[i][j] = 1;} else {// 其它元素是上一行相邻两个元素之和a[i][j] = a[i - 1][j - 1] + a[i - 1][j]; }}}// 打印杨辉三角for (int i = 1; i <= n; i++) {// 每一行的元素for (int j = 1; j <= i; j++) {cout << a[i][j] << " "; // 打印每个元素,并空格分隔}cout << endl; // 每打印完一行就换行}return 0;
}


全生态接入系统技术白皮书)



