对于一个带权连通无向图G=(V,E),生成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有生成树的集合,若T为R中边的权值之和最小的生成树,则T称为G的最小生成树(Minimum-Spanning-Tree.MST)。
两种求法:
Prim 算法(普里姆):
从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。
时间复杂度:O(IV|2)(V绝对值的平方) ---------------------适合用于边稠密图
Kruskal算法(克鲁斯卡尔):
每次选择一条权值最小的边,使这条边的两头连通(原本已经连通的就不选),直到所有结点都连通
时间复杂度:O(|E|log2|E|)---------------------------------------适合用于边稀疏图
例题:A - 最小生成树
Description
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。
Input
第一行包含两个整数 N,MN,M,表示该图共有 NN 个结点和 MM 条无向边。
接下来 MM 行每行包含三个整数 Xi,Yi,ZiXi,Yi,Zi,表示有一条长度为 ZiZi 的无向边连接结点 Xi,YiXi,Yi。
Output
如果该图连通,则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。
Sample 1
| Inputcopy | Outputcopy |
|---|---|
4 5 1 2 2 1 3 2 1 4 3 2 3 4 3 4 3 | 7 |
Hint
数据规模:
对于 20%20% 的数据,N≤5N≤5,M≤20M≤20。
对于 40%40% 的数据,N≤50N≤50,M≤2500M≤2500。
对于 70%70% 的数据,N≤500N≤500,M≤104M≤104。
对于 100%100% 的数据:1≤N≤50001≤N≤5000,1≤M≤2×1051≤M≤2×105,1≤Zi≤1041≤Zi≤104。
样例解释: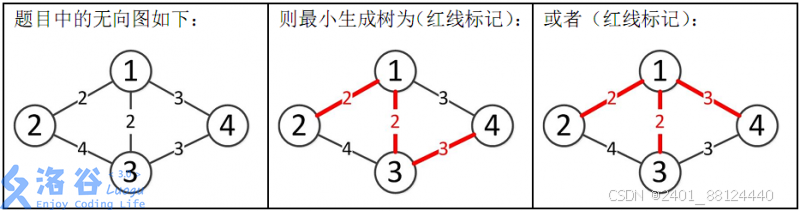
所以最小生成树的总边权为 2+2+3=7
Kruskal算法(克鲁斯卡尔):
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int n, m, min =0,ll=0;
int b[5001];
struct s {int x, y, k;
};
struct s a[200000], d[200000];
//归并排序将其从小到打排序
void digui(int i, int j) {if (i >= j) {return;}int mid = i + (j - i) / 2;digui(i, mid);digui(mid + 1, j);int r = i, l = mid + 1,h=i;while (r <= mid && l <= j) {if (a[r].k < a[l].k) {d[h].k = a[r].k;d[h].x = a[r].x;d[h].y = a[r].y;h++;r++;}else {d[h].k = a[l].k;d[h].x = a[l].x;d[h].y = a[l].y;h++;l++;}}while (r <= mid) {d[h].k = a[r].k;d[h].x = a[r].x;d[h].y = a[r].y;h++;r++;}while (l <= j) {d[h].k = a[l].k;d[h].x = a[l].x;d[h].y = a[l].y;h++;l++;}h = i;while (h <= j) {a[h].k = d[h].k;a[h].x = d[h].x;a[h].y = d[h].y;h++;}
}
//并查集
int cha(int i) {if (b[i] != i) {b[i] = cha(b[i]);return b[i];}else {return b[i];}
}
int main() {scanf("%d %d", &n, &m);for (int i = 0;i < m;i++) {scanf("%d %d %d", &a[i].x, &a[i].y, &a[i].k);}digui(0, m - 1);for (int i = 1;i <= n;i++) {b[i] = i;}int i = 0;while (ll < n-1&&i<m) {if (cha(a[i].x) != cha(a[i].y)) {min+=a[i].k;b[cha(a[i].y)] = b[cha(a[i].x)];ll++;}i++;}if (ll == n - 1) {//有n-1则成立printf("%d\n", min);}else {printf("orz\n");}
}Prim 算法(普里姆):(时间超限)
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int a[5001][5001], n, m, z, x, y, min =0;
int b[5000],c[5001];
int main() {scanf("%d %d", &n, &m);for (int i = 0;i < m;i++) {scanf("%d %d %d", &x, &y, &z);if(a[x][y]==0||a[x][y]>z) {a[x][y] = z;a[y][x] = z;}}b[0] = 1;c[b[0]] = 1;x = 0, y = 1, z = 999999;int w = 0;while (y) {y = 0,z = 10001;for (int i = 1;i <= n;i++) {if(c[i]==0) {for (int j = 0;j <= x;j++) {if (a[b[j]][i] != 0 && a[b[j]][i] < z) {z = a[b[j]][i];w = b[j];y = i;}}}}if (z != 10001) {b[++x] = y;c[y] = 1;min += a[w][y];}else {break;}}if (x == n-1) {printf("%d\n", min);}else {printf("orz\n");}return 0;
}






