此示例展示了如何绘制 Buddhabrot 分形，这是一种与 Mandelbrot 集有些相似的分形曲线。要绘制 Mandelbrot 集，可以使用复数对各种 C 值迭代函数 Z = Z 2 + C。可以证明，如果 Z 的幅度超过 2，则该函数最终趋向于无穷大。
要绘制曼德布洛特集，您需要迭代该函数，并查看函数达到 2 级需要多少次迭代。然后根据迭代次数为点 C 着色。例如，如果您使用 N 种颜色，并且迭代次数为 M 次，那么您可以为该点指定颜色编号 M mod N。
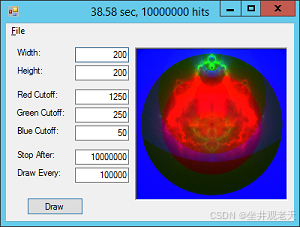
要绘制 Buddhabrot 分形，您可以像往常一样迭代 
的值，但 C 的值是随机选取的。如果函数的幅度在某个点超过 2，则返回并再次迭代该函数。这次，在幅度超过 2 之前，您会对每个 Z 值增加一个计数。完成后，将像素的亮度设置为其命中数除以任何像素的最大命中数的 255 倍。
要获得彩色版本，您需要根据初始值 C 的颜色设置序列中的每个点。在此示例中，如果从 C 到原点的距离小于 1，则程序将点设为红色；如果从 C 到原点的距离小于 √2，则程序将点设为绿色；否则，设为蓝色。
下面的代码显示了主要的DrawBrot方法。
// Draw the Buddhabrot until stopped or
// we plot the desired number of points.
private void DrawBrot()
{// Get parameters.int wid = int.Parse(txtWidth.Text);int hgt = int.Parse(txtHeight.Text);int cut_r = int.Parse(txtRedCutoff.Text);int cut_g = int.
