C数学运算库 GSL的使用-快速傅里叶变换

一、GSL 下载与安装

下载GSL安装文件： http://mirrors.ustc.edu.cn/gnu/gsl/

GSL文档在线：https://www.gnu.org/software/gsl/doc/html/index.html

GSL文档下载：https://www.gnu.org/software/gsl/doc/latex/gsl-ref.pdf

MSVC依赖库：https://download.csdn.net/download/qq_41931610/89708341?spm=1001.2014.3001.5503https://download.csdn.net/download/qq_41931610/89708341?spm=1001.2014.3001.5503

二、快速傅里叶变换

2.1 GSL 中FFT 的定义

正变换（forward）：

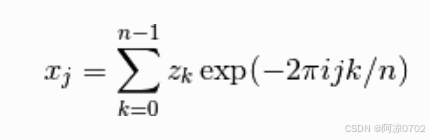
逆变换（inverse）：

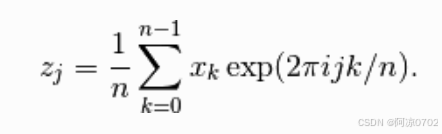
反变换（backward）：

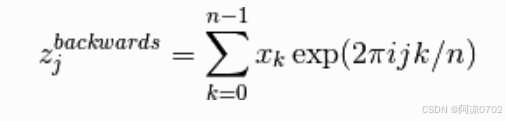
2.2 实数FFT与复数FFT

FFT是计算DFT的快速算法，但是它是基于复数的，所以计算实数DFT的时候需要将其转换为复数的格式。

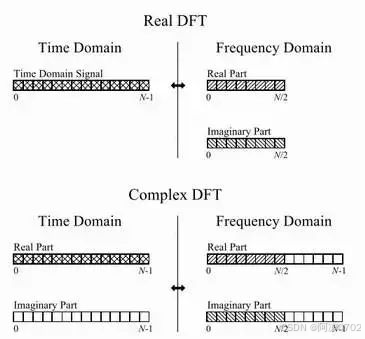
下图展示了实数DFT和虚数DFT的情况，实数DFT将时域中N点信号转换成2个(N/2+1)点的频域信号，其中1个(N/2+1)点的信号称之为实部，另一个(N/2+1)点的信号称之为虚部，实部和虚部分别是正弦和余弦信号的幅度。相比较而言，复数DFT将2个N点的时域信号转换为2个N点的频域信号。时域和频域中，1个N点信号是实部，另1个N点信号是虚部。

如果要计算N点实数DFT，则将这个N个点作为时域中的实部，另取N个0点作为时域的虚部，用FFT计算这样一个复数信号的DFT得到2个N点的频域信号，1个N点是实部另1个N点是虚部，在这两个N点的信号中，从0到N/2个点就是须计算的N点实数的DFT频域。

2.3 复数FFT

分配空间

gsl_fft_complex_wavetable *wavetable = gsl_fft_complex_wavetable_alloc (N);

gsl_fft_complex_workspace * workspace = gsl_fft_complex_workspace_alloc (N);

选择需要的运算

gsl_fft_complex_forward (data, stride, N, wavetable, workspace );
gsl_fft_complex_transform (data, stride, N, wavetable, workspace, sign);
gsl_fft_complex_backward (data, stride, N, wavetable, workspace );
gsl_fft_complex_inverse (data, stride, N, wavetable, workspace );

释放分配空间

gsl_fft_complex_workspace_free (workspace);
gsl_fft_complex_wavetable_free (wavetable);

例子

#include <stdio.h>
#include <math.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_fft_complex.h>#define REAL(z,i) ((z)[2*(i)])
#define IMAG(z,i) ((z)[2*(i)+1])int main (void)
{int i;const int n = 630;double data[2*n];gsl_fft_complex_wavetable * wavetable;gsl_fft_complex_workspace * workspace;for (i = 0; i < n; i++){REAL(data,i) = 0.0;IMAG(data,i) = 0.0;}data[0] = 1.0;for (i = 1; i <= 10; i++){REAL(data,i) = REAL(data,n-i) = 1.0;}for (i = 0; i < n; i++){printf ("%d: %e %e\n", i, REAL(data,i), IMAG(data,i));}printf ("\n");wavetable = gsl_fft_complex_wavetable_alloc (n);workspace = gsl_fft_complex_workspace_alloc (n);for (i = 0; i < wavetable->nf; i++){printf ("# factor %d: %d\n", i,wavetable->factor[i]);}gsl_fft_complex_forward (data, 1, n, wavetable, workspace);for (i = 0; i < n; i++){printf ("%d: %e %e\n", i, REAL(data,i), IMAG(data,i));}gsl_fft_complex_wavetable_free (wavetable);gsl_fft_complex_workspace_free (workspace);return 0;}

2.4 实数FFT

2.4.1 当N为偶数时

complex[0].img = 0

complex[N/2].img = 0

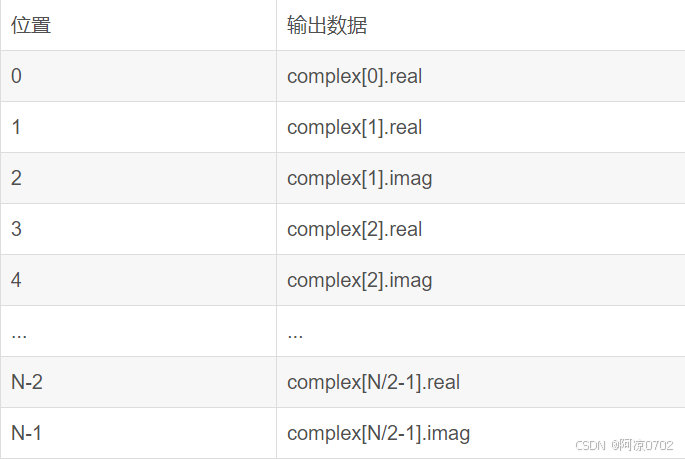
2.4.2 当N为奇数时

complex[0].img = 0

2.4.3 使用

可以把实数数组转换为复数数组，就可以用复数fft 函数来计算了。

int gsl_fft_real_unpack (const double real_coefficient[], gsl_complex_packed_array complex_coefficient[], size_t stride, size_t n)

正变换调用

gsl_fft_real_wavetable * gsl_fft_real_wavetable_alloc (size_t n);
gsl_fft_real_workspace * gsl_fft_real_workspace_alloc (size_t n);int gsl_fft_real_transform (double data[], size_t stride, size_t n, const gsl_fft_real_wavetable * wavetable, gsl_fft_real_workspace * work);void gsl_fft_real_workspace_free (gsl_fft_real_workspace * workspace);
gsl_fft_real_wavetable_free (gsl_fft_real_wavetable * wavetable);

逆变换调用

gsl_fft_halfcomplex_wavetable * gsl_fft_halfcomplex_wavetable_alloc (size_t n);
gsl_fft_real_workspace * gsl_fft_real_workspace_alloc (size_t n);int gsl_fft_halfcomplex_transform (double data[], size_t stride, size_t n, const gsl_fft_halfcomplex_wavetable * wavetable, gsl_fft_real_workspace * work);void gsl_fft_real_workspace_free (gsl_fft_real_workspace * workspace);
gsl_fft_halfcomplex_wavetable_free (gsl_fft_halfcomplex_wavetable * wavetable);