455.分发饼干

题目链接:455.分发饼干
文档讲解:代码随想录
状态:so easy
思路:对胃口和饼干大小排序,小胃口对应小饼干,不满足的话用下一块饼干试探。
题解:
public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int count = 0;int i = 0, j = 0;while (i < g.length && j < s.length) {if (s[j] >= g[i]) {count++;i++;}j++;}return count;}
376. 摆动序列

题目链接:376. 摆动序列
文档讲解:代码随想录
状态:不会,总是有一些我想不到的情况出现
思路:如图
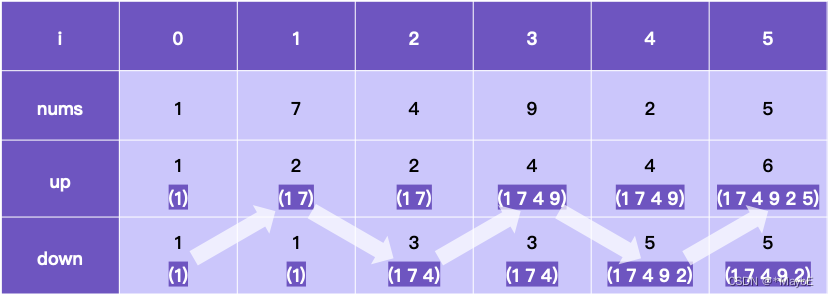
动态规划题解:
class Solution {/*** 输入:nums = [1,17,5,10,13,15,10,5,16,8]* 1, 17, 5, 10, 13, 15, 10, 5, 16, 8* 升 降 升 升 升 降 降 升 降* 降序结尾 0 0 2 2 2 2 4 4 4 6* 升序结尾 0 1 1 3 3 3 3 5 5 5* if 升 {* dp[i][降] = dp[i-1][降]* dp[i][升] = dp[i-1][降]+1* }* if 降{* dp[i][降] = dp[i-1][升]+1* dp[i][升] = dp[i-1][升]* }** @param nums* @return*/public int wiggleMaxLength(int[] nums) {int[][] dp = new int[nums.length][2];int i = 1;for (; i < nums.length; i++) {//dp[i][0]降序结尾//dp[i][1]升序结尾if (nums[i] > nums[i-1]){dp[i][0] = dp[i-1][0];dp[i][1] = dp[i-1][0]+1;}else if (nums[i] < nums[i-1]){dp[i][0] = dp[i-1][1]+1;dp[i][1] = dp[i-1][1];}else{//相等dp[i][0] = dp[i-1][0];dp[i][1] = dp[i-1][1];}}return Math.max(dp[--i][0],dp[i][1])+1;}
}
贪心题解:
public int wiggleMaxLength(int[] nums) {// 如果数组为空或长度小于2,直接返回数组的长度if (nums.length < 2) {return nums.length;}// 初始化两个变量,分别表示上升和下降摆动序列的长度int up = 1;int down = 1;// 遍历数组,从第二个元素开始for (int i = 1; i < nums.length; i++) {if (nums[i] > nums[i - 1]) {// 当前元素大于前一个元素,表示上升摆动up = down + 1; // 上升摆动序列长度为之前下降摆动序列长度加1} else if (nums[i] < nums[i - 1]) {// 当前元素小于前一个元素,表示下降摆动down = up + 1; // 下降摆动序列长度为之前上升摆动序列长度加1}// 如果当前元素等于前一个元素,则跳过,不做任何操作}// 返回上升和下降摆动序列长度的较大值,即为最大摆动序列长度return Math.max(up, down);}53. 最大子序和

题目链接:53. 最大子序和
文档讲解:代码随想录
状态:画蛇添足了,写了两层循环,内层循环的思路已经满足题解了,结果还加了一层循环,结果超时了。。。
错误代码:
public int maxSubArray(int[] nums) {int max = nums[0];for (int i = 0; i < nums.length; i++) {int sum = 0;for (int j = i; j < nums.length; j++) {sum += nums[j];if (sum <= 0) {i = j + 1;sum = 0;}max = Math.max(max, sum);}}return max;}
思路:首先1 <= nums.length <= 105,只能使用nlogn及以下的算法。
- 贪心:将大问题划分成小问题,从第一个数字观察什么时候求和是有效的呢?那就是从第一个数字开始加上后面的数字,如果使sum小于0了,那还不如不加,然后就可以从该位置开始重新求sum,在这个过程中记录max。
- 动态规划:通过定义状态 dp[i] 表示以第 i 个元素结尾的子数组的最大和,并通过状态转移方程 dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]) 来更新每个位置的最大子数组和,同时维护一个变量 maxSum 记录全局最大值。

贪心题解:
public int maxSubArray(int[] nums) {int max = nums[0]; // 初始最大子数组和为数组第一个元素int sum = 0; // 当前子数组的和for (int j = 0; j < nums.length; j++) {sum += nums[j]; // 将当前元素加入到当前子数组和中max = Math.max(max, sum); // 更新最大子数组和if (sum <= 0) {sum = 0; // 如果当前子数组和小于等于0,重新开始计算新的子数组}}return max; // 返回最大子数组和}
动态规划题解:
public int maxSubArray(int[] nums) {int ans; // 存储最终结果的变量int[] dp = new int[nums.length]; // dp数组,dp[i]表示以第i个元素结尾的子数组的最大和dp[0] = nums[0]; // 初始化dp数组的第一个元素为nums[0]ans = dp[0]; // 初始化最终结果为dp[0]// 遍历数组,计算dp数组和最终结果for (int i = 1; i < nums.length; i++) {dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]); // 状态转移方程,选择加上当前元素或者从当前元素重新开始ans = Math.max(dp[i], ans); // 更新最终结果}return ans; // 返回最大子数组和}感悟
很多时候直接想出贪心策略可能有点难,感觉动态规划的状态转移思想可以启发贪心策略的设计。







