【论文阅读28】-CNN-BiLSTM-Attention-（2024）

本文把滑坡位移序列拆开、筛优质因子，再用 CNN-BiLSTM-Attention 来动态预测每个子序列，最后重构出总位移，预测效果超越传统模型。

---

Rubin Wang¹²*, Yipeng Lei²*, Yue Yang²*, Weiya Xu¹², Yunzi Wang²
¹ Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing, China
² Research Institute of Geotechnical Engineering, Hohai University, Nanjing, China

• 教育部地质力学与堤坝工程重点实验室，河海大学，南京，中国
• 河海大学岩土工程研究院，南京，中国

Frontiers in Physics 是 Frontiers Media S.A. 出版社旗下的一本国际性开放获取 (Open Access) 期刊，隶属于 Frontiers 系列期刊体系，涵盖物理学及其交叉学科前沿研究。

[1] Wang R, Lei Y, Yang Y, et al. Dynamic prediction model of landslide displacement based on (SSA-VMD)-(CNN-BiLSTM-attention): a case study[J]. Frontiers in Physics, 2024, 12: 1417536.

摘要

准确预测滑坡位移对于降低和管理相关风险具有重要意义。针对滑坡位移分析中存在的欠分解与过分解问题，以及单一预测模型精度不足的问题，本文提出了一种基于时间序列理论的全新预测模型。该模型将卷积神经网络（Convolutional Neural Network, CNN）、双向长短期记忆网络（Bidirectional Long-Short Term Memory, BiLSTM）与注意力机制相结合，构建了综合性的CNN-BiLSTM-Attention预测模型，充分利用CNN的特征提取能力、BiLSTM的双向时序挖掘能力以及注意力机制的重点关注特性，从而提升滑坡位移预测的精度。

此外，本文引入变分模态分解（Variational Mode Decomposition, VMD）方法，对滑坡位移及其影响因素序列进行分解，利用麻雀搜索算法（Sparrow Search Algorithm, SSA）对VMD参数进行优化，有效减少了主观因素对分解结果的影响，同时保证了分解的完整性。然后，融合最大信息系数（Maximal Information Coefficient, MIC）与灰色关联分析（Grey Relational Analysis, GRA）方法，筛选出关键影响因素，将满足标准的因素序列作为CNN-BiLSTM-Attention模型的输入变量，预测各分量位移，最终通过叠加方式得到累计位移预测值。

研究结果表明，本文所提出的SSA-VMD-CNN-BiLSTM-Attention模型在周期项与随机项位移预测方面均优于单一模型，展现出良好的预测精度，为类似滑坡变形预测提供了可靠的技术参考。

关键词

滑坡位移预测模型；变分模态分解；最大信息系数；双向长短期记忆网络；注意力机制

---

1 引言

滑坡是我国频发且破坏性极强的地质灾害，对周边村民生命财产安全构成长期威胁。滑坡变形演化过程是一个受内在地质条件与外部环境因素共同作用影响的复杂非线性系统[1]。位移是表征滑坡演化趋势与运动特征的直接指标，深入分析滑坡位移变化规律，对于准确识别滑坡演化阶段、有效防范滑坡灾害风险及减少损失具有重要意义[2,3]。

目前，学者们通常基于时间序列理论对滑坡位移序列进行分解，并构建预测模型对各分量位移进行预测[4]。常用的位移分解方法包括滑动平均法[5,6]、经验模态分解（Empirical Mode Decomposition, EMD）[7–9]、集合经验模态分解（Ensemble Empirical Mode Decomposition, EEMD）[10–12]、小波变换（Wavelet Transform, WT）[13–15] 以及变分模态分解（Variational Mode Decomposition, VMD）[16–20]。尽管上述方法在位移序列分解中取得了良好效果，但也存在一定局限性。例如，滑动平均法具有明确的物理意义，但无法分解随机项位移；EMD、EEMD 和 WT 虽克服了滑动平均法的不足，但分解所得分量数量不可控，且各分量物理意义不明确。此外，WT 与离散小波变换（Discrete Wavelet Transform, DWT）在基函数及小波阶数选取方式上存在差异。相比之下，VMD 有效避免了模态混叠现象，能够预先设定分解模态数，且各分量具有清晰物理意义。然而，VMD 分解效果及结果可靠性对参数选取高度敏感。为充分发挥 VMD 算法在分解物理意义明确、适应性强方面的优势，本文利用麻雀搜索算法（Sparrow Search Algorithm, SSA）对 VMD 模型中的惩罚因子 $\alpha$ 和步长 $\tau$ 进行优化，通过周期项位移或影响因素低频分量的样本熵，以及原始位移与重构位移的均方根误差，衡量分解效果与拟合优度。

预测模型的构建在滑坡位移预测精度中起着关键作用。滑坡位移预测模型主要可分为三类：经验模型、统计模型与机器学习模型。基于历史经验的经验模型需大量实测数据与现场试验支撑，且应用条件苛刻。统计模型虽然能有效监测单因素驱动下的滑坡位移，但其对多因素综合作用的预测能力存在不足。随着计算机技术的快速发展，机器学习模型因其计算过程简单、预测精度高、计算成本低以及良好的非线性建模能力，已被广泛应用于滑坡位移预测[21]。例如，Yang 等[22]采用支持向量机（SVM）对滑坡位移进行预测，但个别测点预测误差较大。Du 等[23]基于诱发因素分析构建神经网络位移预测模型；Wang 等[24]将极限学习机（ELM）与随机搜索支持向量回归（RS-SVR）子模型相结合，开发滑坡位移预测模型。Li 等[25]提出集成极限学习方法，预测结果优于单一模型。Wang 等[26]对多种机器学习方法在库区滑坡位移预测中的性能进行了对比研究，表明单一预测精度并不能全面反映模型优劣，集成模型在平均预测精度与稳定性方面表现更优。但上述模型多未充分考虑滑坡演化的动态特性，将滑坡位移预测视作静态回归问题，导致预测精度降低[27,28]。

滑坡位移预测需基于动态预测模型，模拟滑坡位移随时间演化的变化过程。Li 等[28]基于深度信念网络（Deep Belief Network）与指数加权移动平均（EWMA）控制图，构建滑坡位移建模与预测框架，取得了良好效果。长短期记忆网络（Long Short-Term Memory, LSTM）是一种在静态神经网络基础上加入延迟单元与反馈机制的动态神经网络，增强了模型对历史状态及输出的敏感性，尤其适合多因素作用下滑坡位移预测。LSTM 已被广泛用于滑坡位移动态建模与预测[29,30]，研究表明其预测精度优于 BP 神经网络、ELM 与 SVM[31]。但 LSTM 仅依赖历史状态信息，为单向结构。双向 LSTM（Bidirectional LSTM, BiLSTM）在传统 LSTM 基础上引入前向与反向两条神经网络通路，能够同时捕捉时间序列数据的正向与反向依赖关系，提升预测精度[32–34]。

近年来，深度神经网络的发展催生了性能稳定、预测精度高的数据处理与工业预测模型，如卷积神经网络（CNN）与 BiLSTM。CNN-BiLSTM 组合模型融合了 CNN 的特征提取能力与 BiLSTM 的时序记忆功能，在位移预测精度与运算效率方面实现进一步提升[35,36]。Nava 等[37]在不同地理位置、地质条件、观测间隔及测量设备下，利用七种机器学习模型预测四类滑坡位移，结果表明深度学习集成模型性能最优，尤其适用于周期性滑坡如白水河滑坡。Lin 等[38]基于 CNN-BiLSTM 构建联合预测模型，相较于传统 LSTM 和 CNN-LSTM 模型，预测精度更高。Wang 等[39]将 CNN-LSTM 应用于滑坡位移动态预测，发现 CNN-BiLSTM 模型预测精度优于 BP、LSTM 和 GRU 模型。

然而，上述深度学习方法在多维特征数据建模过程中仍存在缺陷，缺少有效的输入特征权重分配机制。实际滑坡变形过程中，输入特征对位移预测的贡献度存在差异，部分特征作用甚微，若赋予过高权重，反而影响模型预测精度。近年来，注意力机制因其在图像识别与机器翻译中的优异表现，逐渐应用于滑坡位移预测。该机制通过对输入特征分配差异化权重，突出重点特征，有效提升预测性能[40]。Tang 等[41]将 BiLSTM 与注意力机制相结合预测滑坡位移，预测效果优于传统 LSTM。

此外，当前多依赖相关性评价方法筛选预测模型输入变量，但易导致评价片面及无关数据干扰，增加模型计算复杂度，降低预测精度。综上，本文以三峡库区白水河滑坡为例，首先采用 SSA-VMD 模型将滑坡位移序列分解为趋势项、周期项与随机项，并对诱发因素序列分解为高频与低频部分。随后，融合最大信息系数与灰色关联分析（MIC-GRA）方法，从不同角度筛选滑坡位移影响因素，最终基于 CNN-BiLSTM-Attention 组合模型预测各分量位移，叠加重构累计位移，并对预测结果进行评价与分析。预测效果验证良好，为滑坡位移预测与预警系统建设提供了可靠技术支撑。

---

2 方法

2.1 位移时间序列加性模型

在统计分析领域，时间序列数据预测是一项极具挑战性的任务，尤其是采用时间序列分析方法时。已有研究 [5, 10, 17, 19, 30] 表明，滑坡累计位移是一种复杂的非线性序列。时间序列分析方法能够将累计位移分解为三个独立部分。主要而言，滑坡变形受趋势项位移的影响最大，而趋势项位移来源于地形、地质构造以及地层岩性等内部地质条件。趋势项位移可视为随时间近似单调递增的函数 [5, 11, 16]。本文探讨了时间对趋势项、周期项和随机项位移的影响。

周期项位移主要受降雨、水库水位等外部因素综合作用，通常表现出近似周期性变化规律，已有研究对此予以证实 [17, 19, 21]。而随机项位移则源于风荷载、车载荷以及地震活动等随机性因素 [22, 29]。

根据时间序列加性模型研究成果，滑坡累计位移可表示为式 (1)：

$$X(t)=T(t)+P(t)+R(t)$$

其中，X(t) 为时间序列位移值，T(t) 为趋势项函数，P(t) 为周期项函数，R(t) 为具有不确定性的随机项函数。

---

2.2 变分模态分解 (VMD) 具体步骤

2014 年，K. Dragomiretskiy 和 D. Zosso 提出了基于 EMD 模型的自适应、非递归信号处理方法——变分模态分解 (VMD) [42]。该方法可将原始输入信号分解为多个具有稀疏特性本征模态函数 (IMF) 分量，且需提前确定模态数量，有效克服了 EMD 方法中存在的端点效应与模态混叠问题。此外，该方法能降低高复杂度、强非线性时间序列数据的非平稳性，使分解后的子序列具备显著稀疏特性。

VMD 中的 IMF 信号形式为调幅调频信号 uₖ(t)，如式 (2) 所示：

$$u_k(t)=A_k(t)\cos \left({\phi }_k(t)\right)$$

其中，φₖ(t) 为相位，Aₖ(t) 为瞬时振幅，φₖ(t) 是非递减函数，且 Aₖ(t) 始终为正值。

输入信号序列与模态之和作为约束变分表达式，具体形式如式 (3)、(4)：

min ⁡ { u k } , { ω k } { ∑ k ∥ ∂ t [ δ ( t ) + j π t ] ∗ u k ( t ) e − j ω k t ∥ 2 2 } \min_{\{ u_k \}, \{ \omega_k \}} \left\{ \sum_k \left\| \partial_t \left[ \delta(t) + \frac{j}{\pi t} \right] * u_k(t) e^{-j \omega_k t} \right\|_2^2 \right\} {uk​},{ωk​}min​{k∑​ ​∂t​[δ(t)+πtj​]∗uk​(t)e−jωk​t ​22​}

$$\text{s.t.}\sum _k{u}_k(t)=x(t)$$

其中，K 为预设模态数量，{ uₖ } = { u₁, ···, uₖ } 为最终分解得到的模态分量，{ ωₖ } = { ω₁, ···, ωₖ } 为各模态分量的中心频率，∂ₜ 表示偏导，δ(t) 为狄拉克函数，* 表示卷积。

为求解上述约束变分问题，引入拉格朗日乘子 λ，将其转化为非约束变分问题，扩展后的拉格朗日表达式如式 (5)：

其中ε用于分解和降低高斯噪声的干扰。利用交替方向乘子迭代算法优化模态分量和中心频率，搜索无约束模型的鞍点，可以得到约束模型的最优解，从而得到K个模态分量。

本研究的目的是利用VMD分解滑坡位移及其影响因素。采用滑坡位移时间序列加性模型，设定模态分量数K=3。影响因子时间序列K=2个模态分量。影响因子的低频分量主要影响滑坡的周期位移，高频分量对随机位移有贡献[19]。利用VMD算法将滑坡位移分解为三个组成部分，关键是要认识到结果可能不具有实际或有形的物理相关性。参数α和K已经确定，它们会影响分解效果和保真度。

高效准确地选择VMD算法中的参数对于位移时间序列的分解至关重要。选择SSA来优化VMD模型中的罚函数α和上升时间步长τ。这种做法有效地避免了主观因素的影响。

2.3.1 样本熵（Sample Entropy）

样本熵（Sample Entropy）是一种用于时间序列分析的复杂性度量指标，由 Richman 等学者提出，用以克服近似熵（Approximate Entropy）在模板匹配过程中存在的偏差问题。该指标通过考虑时间序列中新出现模式的概率与复杂性，有效缓解了近似熵在相似性模板匹配中带来的偏差。与近似熵不同，样本熵不依赖于时间序列长度，因此在不同分析中的结果更具一致性。这一特性使其成为研究人员和工程实践者衡量时间序列数据复杂性的重要工具。

设给定时间序列 x ( t ) = { } x(t)=\{\} x(t)={}，$t=1,2,\dots ,N$，长度为 $N$，其样本熵计算步骤如下：

（1）在时刻 $t$ 构建 $m$ 维向量：
x m ( t ) = { x ( t ) , x ( t + 1 ) , … , x ( t + m − 1 ) } , t = 1 , 2 , … , N − m + 1 x^m(t)=\left\{x(t),x(t+1),\ldots,x(t+m-1)\right\}, \ t=1,2,\ldots,N-m+1 xm(t)={x(t),x(t+1),…,x(t+m−1)}, t=1,2,…,N−m+1

其中，$m$ 为向量的嵌入维数。时间序列子序列之间的距离定义为两子序列对应元素间最大差值的绝对值，记作 $d_{ij}^m$，其计算公式如式（6）所示：
$$d_{ij}^m=\underset{k=0,1,\dots ,m-1}{\max }\left|x(i+k)-x(j+k)\right|,i,j=1,2,\dots ,N-m+1,i\ne j$$

（2）设定相似性容差 $r$，计算子序列 $x_i^m$ 与 $x_j^m$ 之间距离小于 $r$ 的数量占比，记作 $B_i^m(r)$，计算公式为：
$$B_i^m(r)=\frac{\text{num}\left\{d_{ij}^m<r\right\}}{N-m+1}$$
其中， num { } \text{num}\{\} num{} 表示计数函数。

计算所有子序列的平均模板匹配概率 $B^m(r)$，其计算公式为：
$$B^m(r)=\frac{1}{N-m}\sum _{i=1}^{N-m}{B}_i^m(r)$$

（3）将嵌入维数提升为 $m+1$，重复步骤（2）计算相应的平均模板匹配概率 $B^{m+1}(r)$，得到不同维数下的匹配概率。

定义时间序列 $x(t)$ 的样本熵为：
$$\text{SampEn}(m,r)=\underset{N\to \infty }{\lim }\left(-\ln \frac{B^{m+1}(r)}{B^m(r)}\right)$$

当时间序列长度有限时，样本熵为：
$$\text{SampEn}(m,r,N)=-\ln \frac{B^{m+1}(r)}{B^m(r)}$$

其中，$m$ 表示嵌入维数，通常取 1 或 2，$r$ 为相似性容差，一般取 $0.1\sim 0.25{\sigma }_x$，${\sigma }_x$ 为序列的标准差。样本熵值随时间序列复杂性的增加而增大，随序列简单性的提高而减小。

本文利用分解后周期项位移序列的样本熵值作为评价 VMD 算法分解效果的指标，周期项位移序列样本熵值越小，表明分解效果越优。

好！我来帮你把那一段所有多余的反斜杠去掉，保持公式用 $ 包裹，变量前不带反斜杠，调整好的版本如下：

---

2.3.2 雀群优化算法基本原理

雀群搜索算法（Sparrow Search Algorithm，SSA）是一种由 Xue 等人提出的群体智能优化算法 [44]。该算法的优化策略源自麻雀在觅食和反捕食过程中的行为特性。作为一种群体智能算法，SSA 在搜索精度、收敛速度、稳定性以及鲁棒性方面优于多种其他算法。它已成功应用于车间调度、参数优化、图像分类和图形优化等多个领域。在此基础上，本文将 SSA 应用于 VMD 算法中惩罚因子与上升步长参数的自适应寻优。

SSA 将麻雀种群分为发现者、跟随者和哨兵三类角色，其位置更新方式如式 (11)–(13) 所示：

$$X_{i,j}^{t+1}=\{\begin{array}{ll}{X}_{i,j}^t\exp \left(-\frac{i}{\alpha ite{r}_{max}}\right),& R_2<ST\\ X_{i,j}^t+QL,& R_2\ge ST\end{array}\text{\hspace{1em}(11)}$$

$$X_{i,j}^{t+1}=\{\begin{array}{ll}Q\exp \left(\frac{X_{worst}-X_{i,j}^t}{i^2}\right),& i>n/2\\ X_p^t+\left|X_{i,j}^t-X_p^{t+1}\right|\cdot (A+L),& i\le n/2\end{array}\text{\hspace{1em}(12)}$$

$$X_{i,j}^{t+1}=\{\begin{array}{ll}{X}_{best}^t+\beta \left|X_{i,j}^t-X_{best}^t\right|,& f_i>f_g\\ X_{i,j}^t+K\frac{|X_{i,j}^t-X_{worst}^t|}{(f_i-f_w)+\epsilon },& f_i\le f_g\end{array}\text{\hspace{1em}(13)}$$

其中，$t$ 为当前迭代次数，$iter\_max$ 为最大迭代次数，$\alpha$ 为 $(0,1]$ 区间内的均匀随机数，$Q$ 为标准正态分布随机数，$X\_i,j$ 为第 $i$ 只麻雀在第 $j$ 维的位置信息，$L$ 为所有元素为 1 的矩阵，$R_2\in [0,1]$ 为预警值，$ST\in [0.5,1]$ 为警戒阈值，$X\_worst$ 为当前全局最差位置，$X\_p^t$ 为发现者占据的最优位置，$A$ 为多维矩阵元素为 1 或 -1，$n$ 为麻雀种群数量，$X\_{best}^t$ 为当前全局最优位置，$\beta$ 为步长控制参数，$K$ 为 $[-1,1]$ 区间内的均匀随机数，表示麻雀的移动方向，$f_i$ 为当前麻雀适应度，$f_g$ 为当前全局最优适应度，$f_w$ 为当前最差适应度，$varepsilon$ 为一个极小常数。

为了优化 SSA 算法，合理确定适应度函数至关重要。本文通过将 VMD 分解后的子序列重构为 $m$，计算重构序列与原始序列 $M$ 的均方根误差（RMSE）来评价分解的保真度，公式如下：

$$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(x_t-{\hat{x}}_t\right)}^2}\text{\hspace{1em}(14)}$$

其中，$x_t$ 为原始序列在 $t$ 时刻的值，$hat{x}_t$ 为重构序列在 $t$ 时刻的值，$n$ 为序列长度。式 (14) 表明，RMSE 值越小，重构序列 $m$ 与原始序列 $M$ 的误差越小，原始序列的损失也就越小。

本文将样本熵与均方根误差相结合，以更全面反映分解序列的完整性和分解效果，适应度函数表示如下：

$$fitness=RMSE(m,M)\cdot SampEn(IM{F}_2)\text{\hspace{1em}(15)}$$

其中，$RMSE(m,M)$ 为重构序列与原始序列之间的均方根误差，$SampEn(IM{F}_2)$ 为分解后周期项位移序列或影响因子低频部分的样本熵值。SSA 算法以式 (15) 计算得到的值作为适应度值，并通过优化惩罚因子 $alpha$ 与上升步长 $tau$，以获得最优适应度。

优化过程如下：

1. 输入位移时间序列信号。
2. 初始化雀群优化算法参数，随机生成一组 $alpha$ 和 $tau$ 作为麻雀种群的初始位置。
3. 基于当前麻雀位置参数，对位移序列执行 VMD 分解，计算分解后周期项序列或影响因子低频部分的样本熵。
4. 按式 (10) 计算每个麻雀的适应度值，识别当前最优与最差适应度个体，并依据式 (11)–(13) 更新发现者、跟随者与预警个体位置。
5. 重复步骤 3 和 4，直至达到最大迭代次数，输出此时麻雀位置及适应度值作为最优解。

---

2.4 最大信息系数 (MIC)

互信息（Mutual Information，MI）[45] 源于 Shannon 熵理论，是一种用于分析两个随机变量之间统计相关性的方法。它能够有效检测变量间的线性与非线性关系。但由于互信息未标准化，无法量化相关强度，存在一定局限。

为此，本文引入最大信息系数（Maximal Information Coefficient，MIC）。该方法由 Reshef 等人于 2011 年发表在《Science》期刊 [46]，基于互信息拓展而来，能够全面评价变量间的依赖关系，适用于定量刻画线性、非线性甚至非函数型相关关系。

MIC 的基本原理如下：对于两个随机变量 $X$ 和 $Y$，及有限有序数据集 $D(X,Y)=(x_i,y_i),i=1,2,ldots,n$，将数据集 $D$ 中 $X$ 与 $Y$ 的取值区间分别划分为 $xtimesy$ 个网格 $G$，然后计算数据集在该网格下的概率分布 $D|G$，并求取该划分方式下的互信息值 $I(D|G)$。最终，遍历所有可能网格划分，求取最大互信息值，公式如下：

$$I^{\ast }(D,x,y)=\max I(D|G)\text{\hspace{1em}(16)}$$

将 KaTeX parse error: Undefined control sequence: \* at position 3: I^\̲*̲(D, x, y) 标准化，得到特征矩阵元素 $M(D{)}_{x,y}$，公式如下：

$$M(D{)}_{x,y}=\frac{I^{\ast }(D,x,y)}{\log \min (x,y)}\text{\hspace{1em}(17)}$$

不同 $xtimesy$ 网格划分方式下可计算得到不同的 $M(D{)}_{x,y}$，其中最大值即为变量 $Y$ 对 $X$ 的 MIC 值，公式如下：

$$MIC(D)=\underset{xy<B(n)}{\max }M(D{)}_{x,y}\text{\hspace{1em}(18)}$$

其中，$B(n)$ 为网格最大划分数，$n$ 为数据样本容量，通常取 $B=n^{0.6}$ [47, 48]，本文亦采用该值。

---

2.5 CNN-BiLSTM-Attention 组合模型构建

2.5.1 CNN 原理结构

卷积神经网络（Convolutional Neural Network, CNN）是深度学习中应用最广泛的神经网络模型之一【49】。凭借强大的特征学习能力，CNN 可显著减少模型参数数量，因而被广泛应用于图像识别与计算机视觉等领域。近年来，越来越多的研究者将 CNN 有效应用于时间序列分析。该模型通过权值共享和局部连接等特性，显著降低模型训练所需的参数数量，提高模型训练速度，并能高效提取输入数据中的特征信息【50】。

CNN 主要包括卷积层、池化层、全连接层和输出层。卷积层对输入时间序列数据进行非线性操作，提取局部特征信息；池化层通过池化函数降低卷积输出的维度，增强模型的鲁棒性与泛化能力；全连接层将池化层输出映射为固定长度的列向量。本文采用两层一维卷积结构的 CNN，用于特征信息提取，其结构如图 1 所示。

2.5.2 BiLSTM 模型

1997 年，Sepp Hochreiter 等人提出了长短期记忆网络（Long Short-Term Memory, LSTM）。该模型通过门控结构与内部记忆单元，有效解决了循环神经网络（RNN）在长序列训练中存在的梯度消失与梯度爆炸问题【51】。LSTM 模型的控制单元由遗忘门、输入门和输出门组成，其计算公式如式（19）–（24）所示：

• 遗忘门： $f_t=\sigma (W_f[h_{t-1},x_t]+b_f)$ (19)

• 输入门： $i_t=\sigma (W_i[h_{t-1},x_t]+b_i)$ (20)

• 候选状态： ${\tilde{C}}_t=\tanh (W_c[h_{t-1},x_t]+b_c)$ (21)

• 单元状态更新： $C_t=i_t\times {\tilde{C}}_t+f_t\times C_{t-1}$ (22)

• 输出门： $o_t=\sigma (W_o[h_{t-1},x_t]+b_o)$ (23)

• 隐藏状态： $h_t=o_t\times \tanh (C_t)$ (24)

其中，$f\_t$、$i\_t$ 和 $o\_t$ 分别表示遗忘门、输入门和输出门，$W\_f$、$W\_i$、$W\_c$、$W\_o$ 表示各门控单元的权重矩阵，$b\_f$、$b\_i$、$b\_c$、$b\_o$ 表示偏置项，$x\_t$ 表示输入时间序列数据，$\sigma$ 表示 Sigmoid 激活函数，$\tanh$ 为双曲正切激活函数，$C\_t$ 和 $\tilde{C}\_t$ 分别为单元状态和候选状态。

双向长短期记忆网络（Bidirectional Long Short-Term Memory, BiLSTM）在传统 LSTM 模型基础上显著提升，通过前向与反向 LSTM 同时对序列进行学习，从而融合过去和未来时刻的信息，提升预测精度【33,34,52】。BiLSTM 模型结构如图 2 所示。

2.5.3 Attention 机制

注意力机制（Attention）通过为不同特征分配权重，将更大的权重分配给关键信息，较小的权重分配给次要内容，从而提升信息处理效率及模型预测精度【54】。Attention 单元结构如图 3 所示，其具体计算公式可参考文献【53】。

2.5.4 CNN-BiLSTM-Attention 组合模型预测流程

本文提出了一种基于 CNN-BiLSTM-Attention 模型的滑坡位移动态预测方法。该模型采用两层一维卷积层与池化层组成的 CNN 框架，自动提取位移序列内部特征。卷积层高效完成时间序列的非线性局部特征提取，池化层采用最大池化方法对提取的特征进行压缩，生成关键信息。

BiLSTM 隐藏层对 CNN 提取的局部特征进行动态变化学习，并在此基础上迭代提取复杂的全局特征。Attention 机制进一步对 BiLSTM 隐藏层输出的特征赋予不同权重，判断时间信息的重要性，从而挖掘深层时间依赖关系，提升位移时间序列时序特性利用效率。通过保留历史信息、突出关键历史时刻，Attention 机制有效减弱冗余信息对位移预测结果的干扰。

Attention 层输出作为全连接层的输入，最终实现位移预测值的精准输出。网络参数优化过程中，采用 Adam 优化算法对各层参数进行调整，损失函数选用均方误差（MSE）。CNN-BiLSTM-Attention 组合模型结构如图 4 所示。

2.5.5 位移预测流程

基于该模型的滑坡位移预测流程如下：

(1) 使用 SSA-VMD 模型将原始滑坡位移时间序列分解为三个子序列，分别为趋势项位移 $T(t)$、周期项位移 $P(t)$ 和随机项位移 $R(t)$，分解依据最优适应度函数值确定。

(2) 将影响因素序列采用 SSA-VMD 方法分解为低频和高频两个子序列，并依据最优适应度函数值选取最优分解子序列。计算各影响因素分解子序列与各位移子序列间的最大互信息系数（MIC）和灰色关联系数（GRA），综合分析影响因素子序列与位移子序列间的相关性。

(3) 按照各位移项与影响因素的预定序列顺序，将输入数据划分为训练集和验证集，构建并训练单因子 CNN-BiLSTM-Attention 模型用于趋势项位移预测，多因子 CNN-BiLSTM-Attention 模型用于周期项与随机项位移预测。

(4) 最后，将预测得到的趋势位移、周期位移与随机位移值进行累加，形成滑坡累计位移预测结果，并与累计位移监测值对比，评价新模型预测性能。

结合 SSA-VMD 与 CNN-BiLSTM-Attention 的滑坡位移预测模型流程如图 5 所示。

好的！我来把你这段内容翻译成中文，公式里的美元符号 $ 保留，但绝不加反斜杠，方便你直接复制到 Obsidian 里用。以下是翻译：

---

3 案例分析

3.1 白水河滑坡工程地质调查及位移特性分析

白水河滑坡位于三峡库区秭归县，滑坡体呈单斜顺层结构，其南高北低，阶梯状缓倾向长江方向（如图 6 所示）。滑坡后缘高程约 410 m，前缘低于 135 m 水位线。整体滑坡体坡度约为 30°，地形地貌见图 7。自 2003 年监测以来，滑坡多次发生显著变形事件。地质调查表明，白水河滑坡整体呈不规则“U”形，南北长 500 m，东西宽 430 m，滑坡面积约 21.5 × 10⁴ m²，滑动体平均厚度约 30 m，总体体积约 645 × 10⁴ m³，滑动方向约为 20°。如图 8 所示，滑坡每次位移变化均与降雨量增多及库水位剧烈变化密切相关。降雨通过影响岩土强度、物理力学参数及孔隙水压力等因素，作用于滑坡稳定性 [55–57]。库水位通过静水压力、动水压力及孔隙水压力等方式，影响滑坡变形状态 [58,59]。每年 5-9 月为库区汛期，降雨增多，库水位变化幅度及影响范围增大，10 月至次年 4 月为非汛期，降雨稀少，滑坡变形趋于缓和。库水位与降雨的周期性影响使滑坡位移呈现阶梯状特征。

3.2 VMD 滑坡位移分解

本研究中，SSA 算法采用种群规模 50，最大迭代次数 100，惩罚因子 α 与上升时间步长 τ 的优化范围分别设定为 [0.1, 1000] 和 [0, 1]。表 1 给出了优化结果，图 9 和图 10 展示了相应的分解效果。

3.3 滑坡位移影响因子筛选

3.3.1 滑坡位移影响因子分析

结合白水河滑坡变形特征及国内外已有研究，通常将降雨和库水位变化作为滑坡位移的主要影响因素。但如图 8 所示，2015 年滑坡位移增幅最大，当年降雨量和库水位变化幅度却并非最大。这表明滑坡位移不仅仅取决于外部激励强度，更与滑坡自身变形演化阶段密切相关。当滑坡处于相对稳定阶段，即使外力作用强烈，也不易发生大位移；而在不稳定阶段，适度激励便可能引发显著变形 [60,61]。因此，滑坡对外部因素的响应除受激励强度控制外，还与其当前演化阶段密切相关。

在此基础上，本文将滑坡位移演化状态作为预测模型额外输入特征，最终确定的影响指标包括：1 个月累计降雨量 $P\_1$、2 个月累计降雨量 $P\_2$，以及月均库水位高程 $R\_1$、前 1 个月库水位变化幅度 $R\_2$、前 2 个月库水位变化幅度 $R\_3$。为刻画位移演化状态，选取前 1 个月位移值 $S\_1$ 与前 2 个月位移值 $S\_2$。

利用 VMD 算法将各影响因子序列分解为高频和低频部分，高频部分如 $P1U$、$P2U$、$R1U$、$R2U$、$R3U$、$S1U$ 和 $S2U$，作为随机项位移影响因子，低频部分如 $P1L$、$P2L$、$R1L$、$R2L$、$R3L$、$S1L$ 和 $S2L$，作为周期项位移影响因子。分别采用最大信息系数（MIC）与灰色关联度分析（GRA）综合评价影响因子与周期项、随机项位移序列的相关性。

3.3.2 最优 VMD 位移影响因子序列分解

SSA 算法种群规模 50，最大迭代次数 100，惩罚因子 α 和上升时间步长 τ 的优化范围设为 [0.01, 1000] 和 [0, 1]。表 2 给出了优化结果，图 11-14 显示了相应的分解结果。

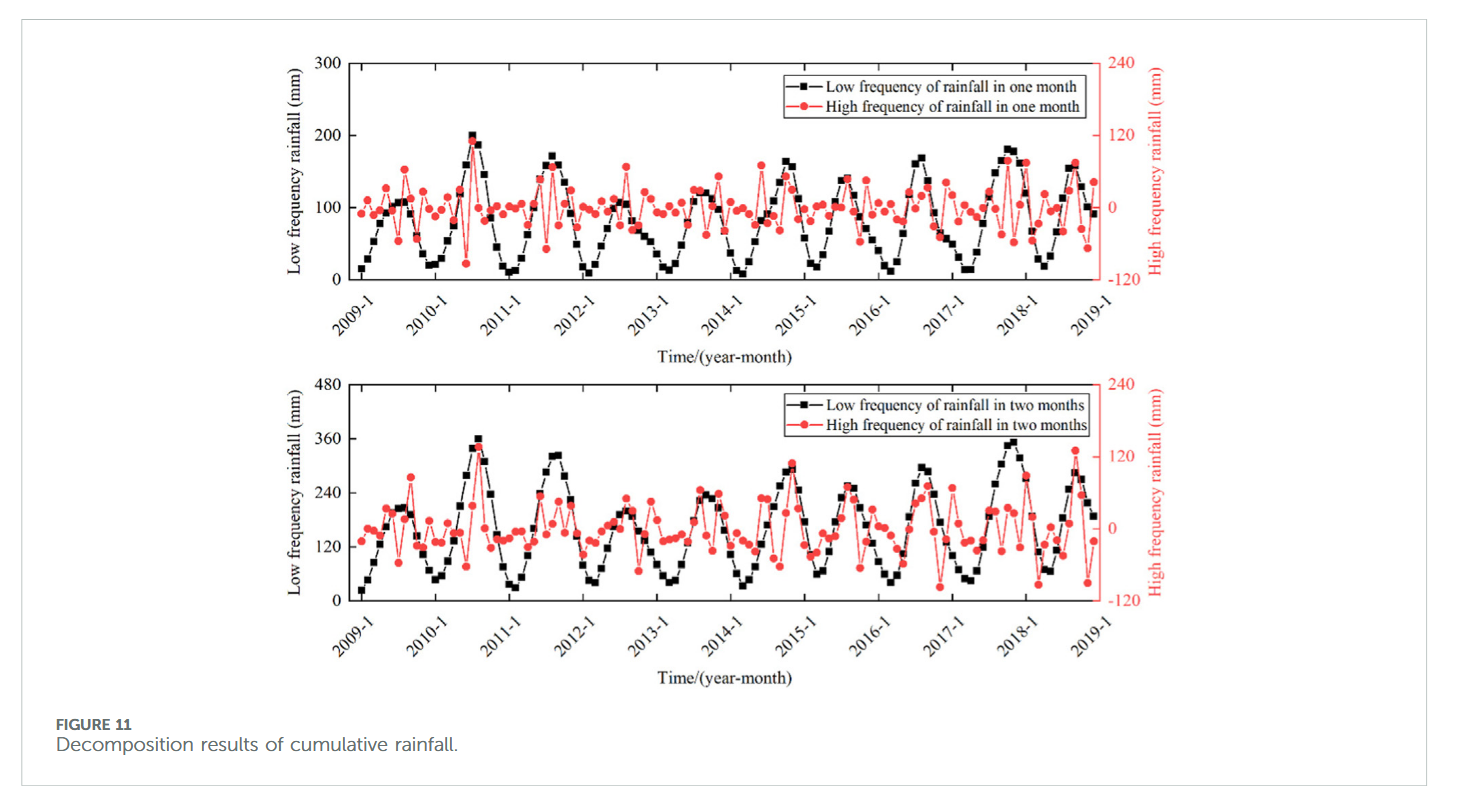
3.3.3 位移与影响因子相关性分析

为了揭示滑坡位移与影响因子的相关性，需对影响因子进行详细分析与分解，筛选高相关因子，以提升模型预测精度和效果。同时，模型训练需保证足够高质量的数据，若引入低相关因子，反而可能引入噪声，削弱预测模型的准确性与有效性。合理选取影响因子可显著提高模型性能与预测精度。

现有研究多采用单一方法评估位移分量与影响因子间相关性，但单一方法仅能从某一角度评判，存在片面性，且易遗漏重要信息。为此，本文采用 MIC-GRA 融合方法对相关性进行综合筛选。表 3 给出了两种方法的计算结果，并通过后续预测对比验证了该方法的优越性。

3.4 位移预测结果与分析

3.4.1 趋势位移预测

滑坡位移受地形、地质结构及岩土性质等因素影响，其趋势位移随时间呈单调递增特性。现有研究多采用多项式函数拟合趋势位移序列，但由于不同阶段变形特性存在差异，常需分段拟合，单一函数难以准确拟合全程趋势位移曲线。

本文基于单因子 CNN-BiLSTM-Attention 模型预测趋势项位移，模型输入包括前 1 个月位移、前 2 个月位移、前 3 个月位移、上月位移变化量以及前 2 个月位移变化量。预测结果如图 15 所示，监测点 ZG118 和 XD01 的 $R^2$ 值分别达到 0.995 和 0.999，对应均方根误差（RMSE）分别为 3.195 和 6.573。

---

3.4.2 周期项位移预测

本文依据最大信息系数（MIC）值大于 0.25 和灰色关联度（GRA）值大于 0.60 的原则，筛选周期项位移序列与低频影响因子序列。多轮筛选与试算后，确定最终输入因子，构建多因子 CNN-BiLSTM-Attention 模型进行训练与预测。预测结果如图 16 所示，监测点 ZG118 和 XD01 的 $R^2$ 值分别为 0.994 和 0.995，对应的均方根误差（RMSE）分别为 1.670 和 1.798。

3.4.3 随机项位移预测

本研究同样依据 MIC 值大于 0.25 和 GRA 值大于 0.60 的原则，从随机项位移序列与高频影响因子序列中筛选相关因子，作为多因子 CNN-BiLSTM-Attention 模型输入进行训练与预测。预测结果如图 17 所示，监测点 ZG118 的 $R^2$ 值为 0.723，RMSE 值为 4.296，监测点 XD01 的 $R^2$ 值为 0.612，RMSE 值为 5.472。

3.4.4 累计位移预测

根据时间序列求和原则，将趋势项、周期项和随机项位移预测结果累加，得到滑坡累计位移预测值。结果如图 18 所示，监测点 ZG118 和 XD01 的 $R^2$ 值分别为 0.975 和 0.988，对应 RMSE 值分别为 12.458 mm 和 9.579 mm。较高的 $R^2$ 和较低的 RMSE 值表明模型预测精度优异，验证了该方法在滑坡位移预测中的有效性。

3.5 对比分析

3.5.1 影响因子选择方法对比

为提升预测性能，本文采用 CNN-BiLSTM-Attention、GRA-CNN-BiLSTM-Attention、MIC-CNN-BiLSTM-Attention 和 MIC-GRA-CNN-BiLSTM-Attention 四种模型，统一条件下对滑坡位移两分量进行预测及对比分析。表 4 给出了不同影响因子选择方法下的预测结果。

从表 4 可知，单独采用 GRA 或 MIC 算法均能有效筛选出高相关性影响因子，且预测精度均优于不筛选模型。将两者结合的 MIC-GRA 算法表现最优，说明 MIC-GRA 融合算法能从两种不同视角筛选相关性强的影响因子，剔除低相关数据，保留高相关性因子，从而显著提升模型预测精度。

3.5.2 周期项位移预测模型对比分析

将 CNN-BiLSTM-Attention 模型预测结果与 BP 神经网络、SVM 等静态机器学习模型，以及 LSTM、BiLSTM、CNN-BiLSTM 等常见深度学习模型预测结果进行对比，结果如表 5 所示。

表 5 显示，CNN-BiLSTM-Attention 模型在周期项位移预测精度方面优于 BP 和 SVM 模型，主要归功于 BiLSTM 动态特性，能够双向捕捉滑坡位移序列的动态变化特征，同时卷积神经网络与注意力机制有效提取关键信息，降低数据复杂度，提升周期项预测准确率。此外，CNN-BiLSTM-Attention 模型同样优于 LSTM、BiLSTM 和 CNN-BiLSTM 模型，说明深度学习方法整体预测精度优于传统机器学习方法，组合模型性能优于单一模型。

3.5.3 随机项位移预测模型对比分析

将 CNN-BiLSTM-Attention 模型在随机项位移预测中的效果与 LSTM、BiLSTM、CNN-BiLSTM 模型进行对比，结果如表 6 所示。

表 6 表明，CNN-BiLSTM-Attention 模型在高频、高波动性的随机项位移预测中表现最佳。相较于 LSTM 和 BiLSTM，CNN-BiLSTM-Attention 模型能更好捕捉时间序列中的非线性特性，依靠 BiLSTM 双向训练优势保留序列关键信息，同时注意力机制可根据不同时间节点权重差异分配，简化数据处理流程，提升随机项位移预测效果与准确性。

---

4 讨论

由于滑坡位移及其致灾因素存在显著的非线性与复杂性，准确评估库区滑坡变形对灾害预警至关重要。本文提出的基于深度学习集成模型与最优变分模态分解（SSA-VMD）相结合的数据驱动预测框架，具备以下两点优势：一是应用 SSA-VMD 算法对滑坡位移序列及其影响因子序列进行分解，有效提升位移时间序列预测模型的预测性能；二是创新性地融合 CNN-BiLSTM-Attention 集成深度学习模型，用于库区滑坡位移预测，该模型整合各单体模型优势，具备更强的非线性与复杂特征提取能力。

尽管现有位移分解方法均取得了较好效果，但本文所提出的 SSA-VMD 模型在随机项位移捕捉方面表现尤为突出。目前，滑坡变形预测精度受限于相关影响因子监测数据不足，且现有位移监测数据主要来自已变形滑坡体，坡体非线性特性导致仅依靠静态历史数据难以实现精准预测。未来研究应着重将实时监测数据接入预测模型，提升预测精度与及时性，增强滑坡预警系统应用价值。

目前，基于单点位移预测方法依然是滑坡变形预测领域的核心方法，但受限于滑坡系统不确定性，传统点预测方法存在不可避免的误差。为此，本文引入预测区间方法，提升滑坡位移预测准确性。虽然本文重点研究库区滑坡及其水文因素影响，未来可进一步扩展考虑土体力学、地震等多种致灾因素，逐步构建具备更强通用性的滑坡位移预测模型。

---

5 结论

本文提出了 (SSA-VMD)-(CNN-BiLSTM-Attention) 模型，融合 SSA-VMD 分解方法与 CNN-BiLSTM-Attention 深度学习模型，应用于滑坡位移序列及其影响因子预测，并以白水河滑坡为案例开展验证。主要结论如下：

(1) 在 VMD 模型中，基于 SSA 算法实现动态参数优化，降低主观假设干扰，避免繁琐的人工调参过程。通过设计融合样本熵与均方根误差的适应度函数，进一步提升 VMD 模型分解结果的可靠性与分解效率。

(2) 基于 SSA-VMD 算法提取滑坡位移与影响因子子序列，深入分析滑坡位移与降雨、水库水位以及滑坡状态之间的耦合关系，基于 MIC 和 GRA 方法计算子序列相关性，并融合 MIC-GRA 筛选高相关性影响因子。结果表明，采用 MIC-GRA 筛选的影响因子作为输入数据，能够显著提升预测模型精度，有效提升输入数据质量，剔除低相关性数据，提高模型预测能力。

(3) 本文创新性地构建 CNN-BiLSTM-Attention 集成预测模型，整合 CNN、BiLSTM 和 Attention 机制优势，分别实现滑坡位移数据特征提取、双向时序建模与动态权重分配，优化滑坡位移预测流程。实证结果表明，所建模型预测精度优于单一与双组合模型，能够更好地捕捉滑坡位移阶段性演化特征，为滑坡预测与预警应用提供基础支撑。