1

2






3

欧拉角是描述三维空间中刚体或坐标系之间相对旋转的一种方法。它们由三个角度组成,通常表示为:
• 偏航角(Yaw):绕垂直轴(通常是z轴)的旋转,表示偏航方向的变化。
• 俯仰角(Pitch):绕横向轴(通常是y轴)的旋转,表示俯仰角度的变化。
• 翻滚角(Roll):绕纵向轴(通常是x轴)的旋转,表示翻滚角度的变化。
欧拉角的命名和定义可能会根据不同的应用领域和约定有所不同。例如,在航空领域,偏航、俯仰和翻滚是常用的术语,而在机器人学中,可能会使用不同的轴命名。
欧拉角的优点是直观易懂,但它们也存在一些局限性,比如在某些情况下会出现“万向锁”(Gimbal Lock)问题,即当两个轴的旋转角度相同时,会导致一个自由度的丢失,使得旋转变得不确定。
除了欧拉角,还有其他描述旋转的方法,如四元数(Quaternion),它能够避免万向锁问题,并且在计算机图形学和机器人学中广泛使用。
4















5







6



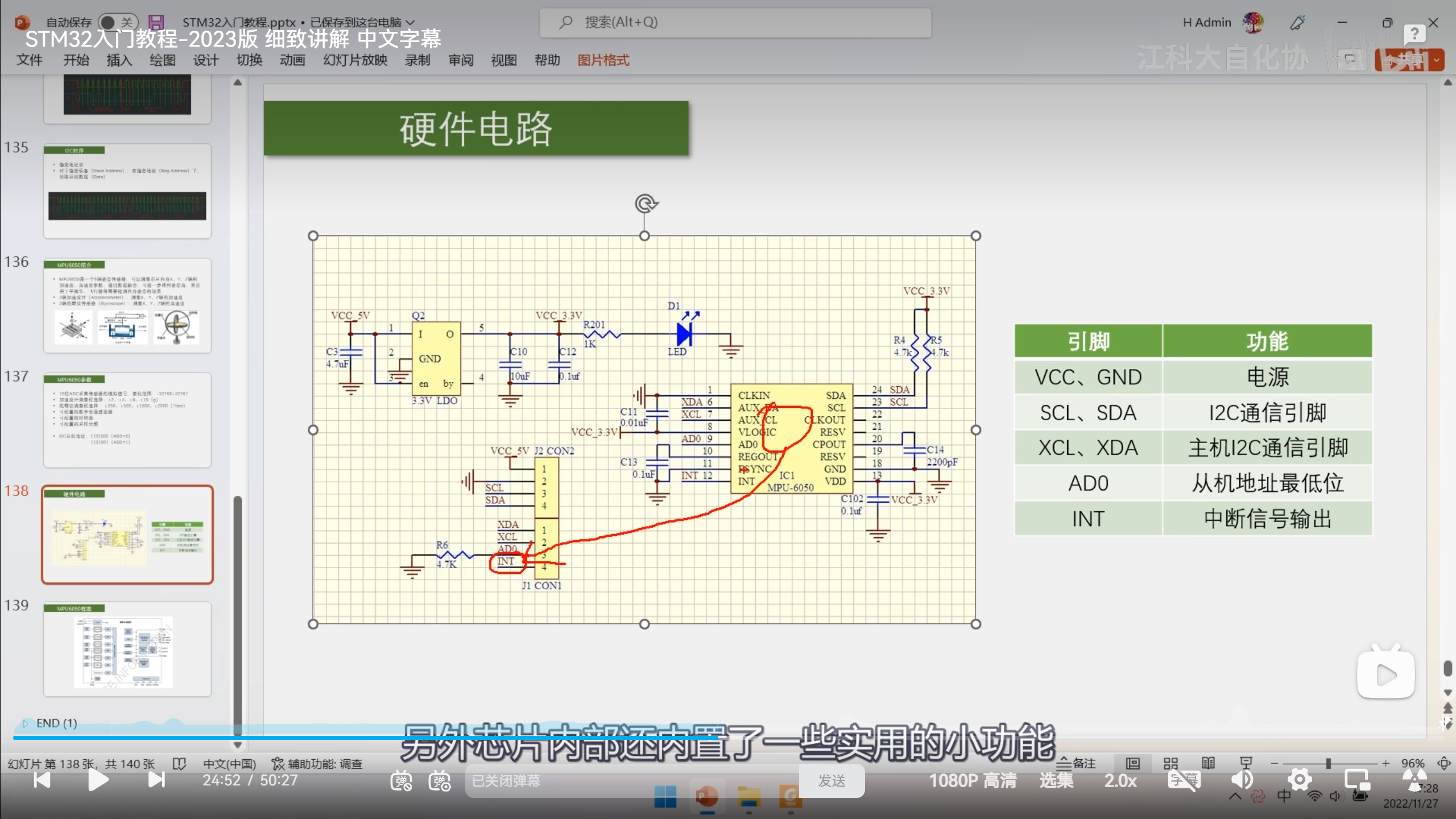
7关于AD0

8

9



10


11



12


13





14![]()






15



16












17





18








19










20


21

22









