【强化学习】#7 基于表格型方法的规划和学习

主要参考学习资料：《强化学习（第2版）》[加]Richard S.Suttion [美]Andrew G.Barto 著

文章源文件：https://github.com/INKEM/Knowledge_Base

本章更是厘清概念厘到头秃，如有表达不恰当之处还请多多指教——

概述

• 环境的分布模型用于规划，样本模型用于学习，许多算法在规划和学习之间可以进行迁移。
• Dyna架构引入模型学习，将与规划相关的间接强化学习与学习代表的直接强化学习集成起来。
• 优先遍历根据贝尔曼误差判断价值估计更新的优先级进行顺序更新。
• 期望更新考虑所有可能发生的转移，采样更新考虑采样得到的单个转移样本。
• 轨迹采样是一种基于同轨策略分布的采样更新。
• 实时动态规划是一种基于轨迹采样的异步动态规划。
• 后台规划独立于环境交互进行，而决策时规划针对环境交互的当前状态进行规划。
• 预演算法是一种基于蒙特卡洛控制的决策时规划算法。
• 蒙特卡洛树搜索是一种使用树策略进行迭代式树展开的预演算法。
• 利用启发式函数指导搜索方向，显著减少计算量的优化搜索方法被称为启发式搜索。

在我们讨论过的强化学习方法中，既有具备环境模型的方法，例如动态规划，也有不具备环境模型的方法，例如蒙特卡洛方法和时序差分方法，这些方法分别被称为基于模型和无模型的强化学习方法。基于模型的方法主要依赖规划，而无模型的方法主要依赖学习。除此之外，这些强化学习方法都是表格型的，它们都用表格（数组或字典）存储状态或“状态-动作”二元组的价值。上一章我们将时序差分方法和蒙特卡洛方法用$n$步方法统一了起来，本章我们的目标是将基于模型的方法和无模型的方法整合起来。

模型和规划

环境的模型是一个智能体可以用来预测环境对其动作的反应的任何事物。给定一个状态和一个动作，作为环境的反应结果，模型能产生后继状态和下一个收益的预测。如果模型是随机的，那么后继状态和下一个收益就有好几种可能。一些模型不仅能给出所有可能的结果，还能给出它们的完整概率分布，这种拥有环境全局信息的模型被称为分布模型；另一些模型无法给出结果的概率分布，而是一个黑箱，它只能利用状态和动作采样出一种可能的结果，并通过多次采样估计分布，这种只掌握来自环境的部分样本的模型被称为样本模型。分布模型仅适用于能够高效、精确地掌握环境特性的情况，而其余计算十分复杂或无法求解的环境特性则只能使用样本模型。所谓无模型的强化学习方法本质上是依赖样本模型的，但它仅将样本模型视为一个数据生成器，或者说是与真实环境交互的桥梁，无法进行解析。而基于模型的方法准确来说则是基于分布模型的。

模型的作用是产生经验。给定一个开始状态和动作，一个样本模型生成一个可能的转移，而分布模型会根据发生的概率产生所有可能的转移。给定一个开始状态和一个策略，一个样本模型可以生成一幕事件，而一个分布模型可以生成所有可能的幕和它们发生的概率。

规划是以环境模型为输入，并生成或改进与其进行交互的策略计算过程。

$$模型\stackrel{规划}{\to }策略$$

在人工智能中有两种不同的规划方法。第一种是状态空间规划，即在状态空间中寻找最优策略或实现目标的最优决策路径，每个动作都会引发状态之间的转移，价值函数的定义和计算都是基于状态的；第二种是方案空间规划，即在已有的方案空间中进行搜索和优化，为此我们要将策略表示为参数化函数。方案空间规划很难有效地应用于随机性序列决策问题，而这是强化学习的重点，所以不会在本系列中进一步讨论。

所有的状态空间规划算法有两个基本的思想：

• 利用计算价值函数作为改善策略的关键中间步骤。
• 通过基于模拟经验的回溯操作来计算价值函数。

$$模型\to 模拟经验\stackrel{回溯}{\to }价值函数\to 策略$$

所有状态空间规划方法都适用于上图这种结构，只是它们所做的回溯操作、执行操作的顺序以及回溯的信息被保留的时间有所不同。

现在我们可以将开头提到的基于模型的和无模型的方法分别依赖的规划和学习统一起来。规划和学习的核心都是通过回溯操作评估价值函数，不同之处在于规划利用分布模型仿真出的模拟经验，学习利用环境产生的真实经验，这种差异进一步导致了许多其他的差异。但是除此之外，规划和学习在结构上是通用的，这意味着许多思想和算法可以在规划和学习之间迁移，例如从分布模型中仿真的模拟经验也能像真实经验作为学习方法的输入。将$Q$学习的流程迁移到分布模型上，利用对分布模型的采样作为$Q$方法的经验输入，我们得到了随机采样单步表格型Q规划算法，其流程如下：

Dyna

Dyna-Q

利用分布模型采样的优点是无需真实交互成本，可并行生成大量数据加速训练，但如果分布模型的建立存在误差，也会传播到策略中；由样本模型从真实环境中采样的优点是数据直接反映真实环境，无模型偏差，但数据获取成本高。而Dyna-Q是一种整合了分布模型与样本模型、规划与学习的特性，交替使用模型采样和环境采样的架构，使得二者的优缺点得到了良好的互补。

Dyna-Q的核心思想是，对一个智能体来说，经验可以扮演两个角色，它能用来改进模型，或是直接更新价值函数和策略。前者称为模型学习，后者则称为直接强化学习。改进后的模型则通过规划影响价值函数和策略，这种与规划相关的方式称为间接强化学习。下图展示了经验、模型、价值和策略之间的可能关系：

直接强化学习类似于试错学习和被动的反应式决策，而间接强化学习则代表了原理认知和主动的预谋性规划。

Dyna-Q的模型学习方法也是基于表格的，并且假设环境是确定的。在每次转移$S_t,A_t\leftarrow R_{t+1},S_{t+1}$之后，模型在它的表格中会为$S_t,A_t$建立条目，记录环境在这种情况下产生的转移结果的预测值$R_{t+1},S_{t+1}$。规划过程中，算法将随机从模型之前学习到的“状态-动作”二元组进行采样并返回历史观测值。除此之外，Dyna-Q的规划方法是上一节给出的随机采样单步表格型$Q$规划方法，直接强化学习方法是单步表格型$Q$学习（即时序差分学习一章中的$Q$学习）。

上图展示了一般的Dyna架构。从概念上讲，规划、动作执行、模型学习和直接强化学习在Dyna的智能体中是并行进行的，但在串行计算机中我们需要指定它们的发生顺序。动作执行、模型学习和直接强化学习过程只需要很少的计算，而规划则需要计算密集的迭代过程，因此我们在每次循环中先执行前者，最后将剩余的计算用于规划。表格型Dyna-Q算法的伪代码如下，其中$Model(s,a)$基于“状态-动作”二元组$(s,a)$预测后继状态和收益：

由此可见，模拟规划的过程就相当于记住之前的经验并重复利用，将一次真实交互的数据用于多次更新，减少冗余探索和重复试错。利用从真实环境中交互获得的样本构建分布模型来进行规划，和依赖交互进行学习相比，是一种节省交互成本、提升数据利用率和计算效率的手段，这在诸如机器人控制、自动驾驶这类真实交互成本高的场景中是很适用的。

Dyna-Q+

Dyna-Q假设环境是确定的，此时模型总是被填充完全正确的信息。但在更多时候我们没有这么幸运，以下这些原因都会导致模型错误：

• 随机环境中只有数量有限的样本会被观察到。
• 模型用于近似环境的函数泛化能力较差。
• 环境发生改变且新的动态特性尚未被观察到。

当模型错误时，规划过程就可能计算出次优的策略。

在某些情况下，规划计算出的次优策略能使得Dyna-Q很快发现并修正模型错误，例如环境变化导致原始最优策略的回报大大降低，模型能很快沿着策略所在路径感知到自身信息和环境不匹配，进而修正错误。但如果这种变化对原始最优策略没有影响，而是产生了原始最优策略之外的捷径，那么Dyna-Q将很难摆脱对原始最优策略的依赖去探索更优的策略。

这个例子中的问题是试探与开发困境的另一种版本。在规划中，试探意味着尝试那些可能改善模型的动作，开发意味着以当前模型的最优方式来执行动作。我们希望智能体通过试探发现环境的变化，但又不希望试探得太多使得平均性能大大降低，因而很难找到一个完美又实用的解决方案。

Dyna-Q+采用的启发式方法在一定程度上克服了这种问题。Dyna-Q+的智能体会对每一个“状态-动作”二元组进行跟踪，记录它自上一次在与环境进行真实交互以来已经过了多少时刻。时间越长，我们就越有理由推测这个二元组相关的环境动态特性会产生变化，也即关于它的模型是不正确的。

为了鼓励测试长期未出现过的“状态-动作”二元组，一个和未出现时间相关的“额外收益”将会提供给智能体。如果模型记录的单步转移收益为$r$，而这个转移在$\tau$时刻内没有尝试，那么在更新时就会采用$r+\kappa \sqrt{\tau }$的收益，其中$\kappa$是一个比较小的正数。这会鼓励智能体不断试探所有可访问的状态转移，甚至使用一长串的动作完成这种试探。

优先遍历

对于上一节介绍的Dyna智能体，模拟经验中的转移是从所有先前经历过的每个“状态-动作”二元组中随机均匀采样得到的。均匀采样通常不是最好的，如果模拟转移和价值函数更新集中在某些特定的“状态-动作”二元组上，则规划可能会高效得多，根据某种更新迫切性的度量对更新进行优先级排序便是优先遍历的基本思想。

直观地考虑，我们可以认为以下情况的“状态-动作”二元组是值得优先遍历的：

• 其更新对策略具有较大的影响（例如接近目标或危险的收益显著的状态）
• 其价值估计的误差较大

符合这两种情况的动“状态-动作”二元组，其价值估计在遍历后往往会产生较大的变化量，回顾$Q$函数的更新公式

$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma \underset{a}{\max }Q(S_{t+1},a)-Q(S_t,A_t)]$$

则其优先级可以用$\alpha$后的部分来表示

$$priority(S_t,A_t)=|R_{t+1}+\gamma \underset{a}{\max }Q(S_{t+1},a)-Q(S_t,A_t)|$$

该优先级衡量标准也称为贝尔曼误差。贝尔曼误差越大，当前估计值越不准确，则应该尽快更新。反之则当前估计值已接近最优，可稍后更新。通常我们会设定一个阈值$\theta$，只有贝尔曼误差超过$\theta$时，估计值的更新才会按优先级进入优先遍历队列。

除此之外，如果智能体在与环境交互时将一个“状态-动作”二元组$(s,a)$放入优先遍历队列，那么我们也可以推断，在规划中，对$(s,a)$的估计更新后，以$s$为可能的后继状态的“状态-动作”二元组$(\bar{s},\bar{a})$的贝尔曼误差将会受到影响，因此可以立刻对所有$(\bar{s},\bar{a})$评估优先级，判断它们是否要在当前轮规划中得到更新，这样就无需等到下一次与环境交互时再考虑了。

在确定性环境下的优先遍历算法的伪代码如下：

但是当环境随机时，优先遍历将采用期望更新，这可能会浪费大量计算来处理低概率的转移。

期望更新与采样更新

目前我们关注的单步更新方法主要在三个维度上有所区分：

• 更新状态价值还是动作价值
• 估计任意给定策略的价值还是最优策略的价值
• 采用期望更新还是采样更新

期望更新会考虑所有可能发生的转移，而采样更新仅仅考虑采样得到的单个转移样本。

在没有分布模型的情况下，进行期望更新是不可能的，我们只能使用采样更新作为其替代方法。但是拥有分布模型也不意味着期望更新就比采样更新更适合，期望更新肯定会产生更好的估计，因为它们不会受到采样误差的影响，但是它们也需要更多的计算，而计算往往是规划过程中的限制性资源。要正确评估期望更新和采样更新的相对优势，我们必须控制不同的计算量需求。

以$Q$函数的更新为例，在实践中，价值函数更新操作所需的计算量通常由需要$Q$函数评估的“状态-动作”二元组的数量决定。对于一个特定的初始二元组$(s,a)$，设$b$是分支因子（即对于所有可能的后继状态$s^{\prime }$，模型估计的概率$\hat{p}(s^{\prime }|s,a)>0$的数目），则这个二元组的期望更新需要的计算量大约是采样更新的$b$倍。

在具有许多“状态-动作”二元组的大尺度问题中，期望更新往往会消耗非常长的时间，这种情况下我们最好先进行若干次采样更新，而不是直接进行期望更新。那么在相同的计算量下，进行期望更新和进行$b$倍次数的采样更新哪个效果更好？

上图展示了在不同分支因子$b$下，期望更新和采样更新的估计误差对计算次数的函数变化。其中估计误差是对一个“状态-动作”二元组的价值估计误差，对一个可能后继状态的动作价值估计取最大值视为一次计算。采样更新每次计算都会更新估计，而期望更新只有计算完所有$b$个可能后继状态才会更新估计。我们假设所有$b$个后继状态等概率发生，初始估计误差为$1$，后继状态的价值是正确的。则期望估计在$b$次计算后误差才降至$0$，而采样更新则很快就能改善估计，且随着$b$值的增大，采样更新仅采样了一小部分就收敛到了和期望更新差不多的效果。在这种情况下，采样更新会使得误差以比例系数$\sqrt{\frac{b-1}{bt}}$减小，其中$t$是已经进行过的采样更新次数。这表明，对于拥有很大的随机分支因子并要求对大量状态价值准确求解的问题，采样更新可能比期望更新要好。

轨迹采样

为了更高效地分配状态更新过程中的算力，我们介绍了优先遍历，但优先遍历的期望更新仍可能带来复杂的计算量。

对于一个控制问题，其目标是找到最优策略，而不是像预测问题一样评估给定的策略。这时可能存在一些状态，来自任何初始状态的任何最优策略都无法到达它们，例如下棋时，大部分无规律的棋局通常不会出现。对于这些不相关的状态，我们就不需要指定最优动作。我们需要的是最优部分策略，即策略对于相关的状态是最优的，而对于不相关的状态可以指定任意的甚至是未定义的动作。而轨迹采样可以很好地筛选出需要得到更新的相关状态。

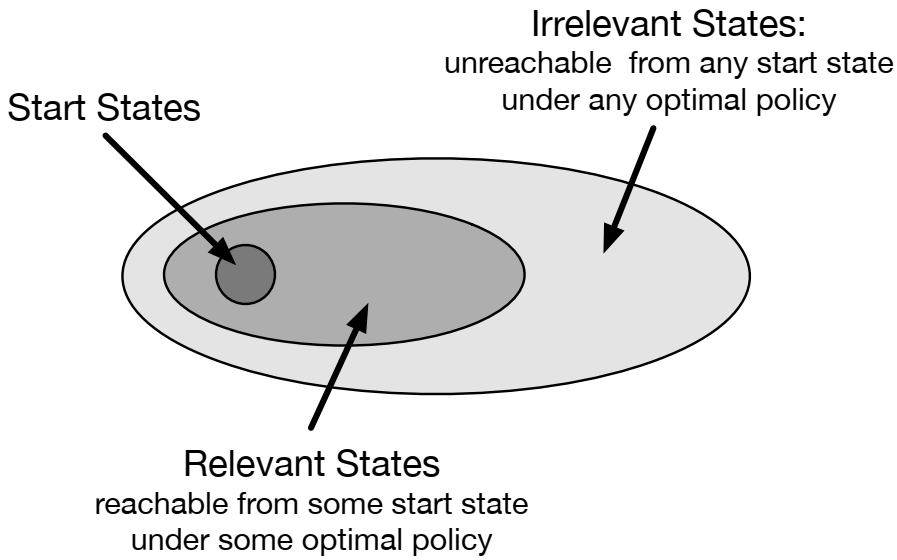
轨迹采样相当于有模型版本的蒙特卡洛方法，如同我们引入随机采样单步表格型Q规划的方式一样，它是一种学习方法到规划方法的迁移，利用模型产生的模拟经验而不是与环境交互的真实经验作为算法的输入。轨迹采样借助模拟生成经验来进行回溯更新。给定一组初始状态，样本动作由当前策略给出，样本状态转移和收益则都由模型给出，模型将持续模拟仿真直到终止状态。

从另一个角度讲，轨迹采样是一种基于同轨策略分布给出，即状态被采样更新的概率分布由在对应策略在任务中的执行情况决定。聚焦于同轨策略分布可能是有益的，因为这使得空间中大量不重要的区域被忽略。但这也可能是有害的，因为这使得空间中某些相同的旧区域一次又一次地被更新。

我们在同一个任务下对二者的效果进行比较。对$|\mathcal{S}|$个状态中的每个状态，有两个可能的动作，每个动作都导致$b$种后继状态中的一个。针对每个“状态-动作”二元组，分支因子$b$相同，而$b$种后继状态的概率分布不同。每一次转移的期望收益从一个标准高斯分布中采样得到，在所有转移中，跳到终止状态结束整幕交互的概率为$0.1$。

上图展示了在不同$b$和$|\mathcal{S}|$下，同轨策略分布（on-policy）和均匀分布（uniform）超过200次试验的平均结果，二者迭代的策略均为$ϵ$-贪心策略（$ϵ=0.1$）。由此可见，同轨策略分布在初始阶段规划速度更快，但长期看却变化迟缓，$b$越小、$|\mathcal{S}|$越大时这个效应就越强。这是因为在短期内根据同轨策略分布进行采样有助于聚焦于接近初始状态的后继状态，而长期下，通常发生的各种状态都已经有了正确的估计值，对它们采样的效益是较低的。尽管上述结果不能形成一般性的结论，但它们确实表明，根据同轨策略分布的采样对于大尺度问题可能具有很大的优势。

实时动态规划

实时动态规划（RTDP）是动态规划（DP）价值迭代算法的同轨策略轨迹采样版本。传统DP需要在每一轮中对所有状态进行更新，而RTDP是异步DP的一个例子，其对状态的更新顺序是由模拟轨迹中状态被访问的顺序决定的。

轨迹采样给RTDP带来的是，对于满足某些合理条件的特定类型的问题，RTDP可以保证找到相关状态下的最优策略，而无须频繁访问每个状态，甚至可以完全不访问某些状态。事实上，在某些问题上，只需要访问一小部分状态，这对于大尺度状态集的问题来说可能是一个很大的优势，因为它们的单次遍历也是不可行的。

使得RTDP可以收敛于对所有相关状态的最优策略的前提条件如下：

• 每个目标状态的初始值（初始价值估计）为零。
• 存在至少一个策略，保证从任何初始状态都能够达到目标状态。
• 从非目标状态跳出的转移（或者说在到达目标状态前的每次状态转移）所对应的收益都严格为负。
• 所有初始值都大于等于其最优值（由于上一个条件，可以通过简单地将所有初始值设置为零来满足）。

决策时规划

本章目前讨论的以动态规划和Dyna为代表的方法所采取的规划方式为后台规划。后台规划在非交互时段进行，按照独立于环境交互的更新方式，用模型生成模拟数据用以优化策略或价值函数。

规划过程的另一种运行方式是在与环境交互的过程中遇到状态$S_t$之后才开始并完成规划，其计算后将返回一个动作$A_t$。智能体执行动作$A_t$后转移到状态$S_{t+1}$，而下一轮规划过程也将从$S_{t+1}$开始并返回$A_{t+1}$，以此类推。这种与环境交互相关，聚焦于特定状态的规划被称为决策时规划。

在决策时规划中，智能体与环境交互并不依赖于固定的策略，而是根据当前状态随机应变。决策时规划会以当前状态$S_t$为起点，对每个候选动作$a$模拟多条轨迹并根据每一步的收益计算它们的折扣回报，选择回报值最高的动作返回。如果模拟轨迹只计算$S_t$之后未到达终止状态的$n$步回报，则最后一个状态的价值估计将来源于预训练策略或价值网络（例如棋局胜率）。一轮规划过程结束之后，其存储的规划结果将被丢弃，下一时刻的状态将重新被评估。

后台规划的计算资源利用率高，策略具有全局一致性，但其无法快速适应环境突变，且可能浪费计算在无关状态上。决策时规划实时适配当前状态，策略具有高灵活性，因而适用于复杂多变的环境，但需要考虑计算延迟带来的实时性问题。

预演算法

预演算法是一种将预训练策略$\pi$，也叫预演策略，应用到智能体与环境交互当中的决策时规划算法。一个有效的预演算法可以在预演策略的基础上修正的局部缺陷，增强动态适应性，进而提升其实时表现。

预演算法的核心思想是动态规划一章中介绍的策略改进定理：

预演算法会生成一系列拟改进的预演策略${\pi }^{\prime }$，并通过$n$步时序差分（或蒙特卡洛）方法评估它们的$q_{\pi }(s,{\pi }^{\prime }(s))$，从而选择更优的动作。具体而言，针对当前状态$S_t$，预演算法将由随机生成的状态转移生成一系列模拟轨迹，即对$S_t$采样一系列候选动作（包括预训练策略$\pi$会选择的动作），每个候选动作产生相应的状态转移之后将继续遵循$\pi$模拟$n$步轨迹，并计算其多次模拟的$n$步回报平均值作为$\hat{Q}(S_t,a)$，最终选择模拟轨迹回报最高的动作$a^{\ast }$。当每个候选动作模拟的次数足够多时，$\hat{Q}(S_t,a)$将逼近$q_{\pi }(s,a)$，这相当于在局部范围（当前状态的有限个动作）内对$\pi$进行了隐式的策略改进。

由此可见，一个更好的策略改进意味着评估更多的动作以包含最优动作、模拟更多的步数以逼近真实回报、模拟更多的次数以逼近真实价值，也就意味着耗费更多的事件，平衡这些因素在任何预演算法的应用中都是很重要的。不过由于回报的计算是相互独立的，因此可以在多个独立的处理器上并行地进行多次模拟。当模拟效果足够逼近时，预演算法甚至在可以不需要预训练策略及其价值估计，或者说采用随机策略的情况下，只依赖模拟返回的结果也能拥有较好的实时表现。

蒙特卡洛树搜索

为了提升预演算法的效率，我们需要对模拟轨迹的采样生成方法进行设计。蒙特卡洛树搜索（MCTS）通过迭代式树展开，可以高效寻找最优动作。

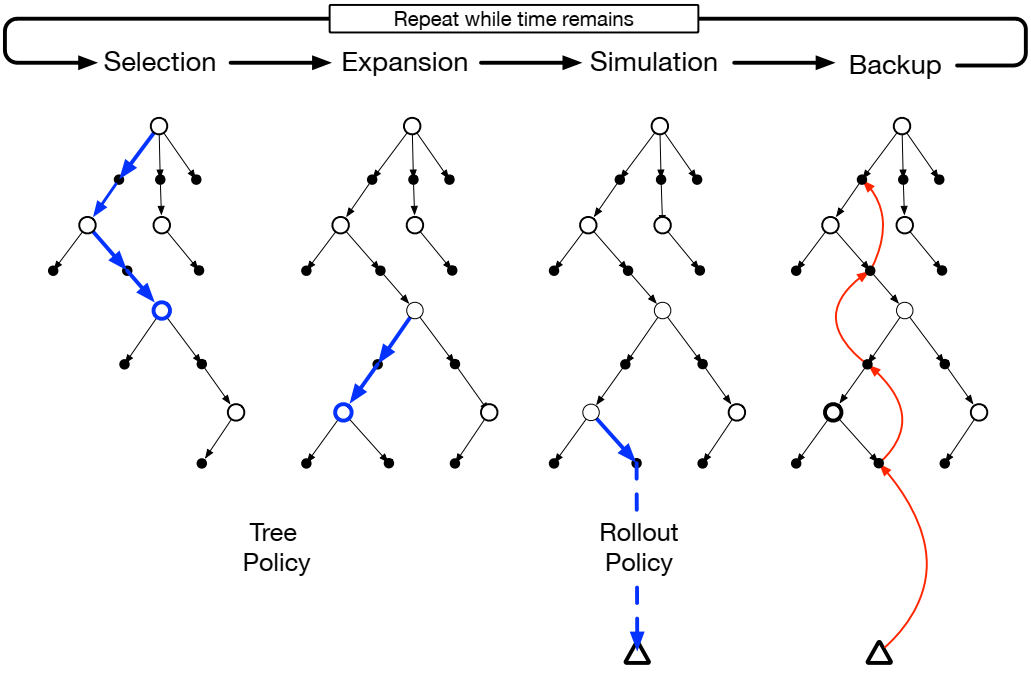
一个基本版的MCTS的每一次迭代中包括下面四个步骤：

• ①选择（Selection）：从根节点出发，根据树策略选择子节点，直到遇到未完全展开（存在未尝试的动作）的节点或叶节点。
  • 树策略可以是$ϵ$-贪心策略，但一个更常用的选择是基于置信度上界（UCB）的动作选择，在多臂赌博机一章中提到。UCB对动作的潜力进行评估，平衡了试探与开发。这里采用的一种基本策略如下：
  • $A\dot{=}\underset{a}{\mathrm{argmax}}\left(\frac{Q_i}{N_i}+c\sqrt{\frac{\ln N_p}{N_i}}\right)$
  • 其中$Q_i$为节点$i$的累计回报，$N_i$为节点$i$的访问次数，$N_p$为父节点的访问次数，$c$为探索系数（通常设为$\sqrt{2}$）。
• ②扩展（Expansion）：若当前节点未完全展开，则选择一个新动作$a$，扩展一个新子节点$s^{\prime }$。
  • 新增节点的初始值为$Q_i=0,N_i=0$。
• ③模拟（Simulation）：从新节点$s^{\prime }$出发，使用预演策略模拟至终止状态，记录其回报$G$。
• ④回溯（Backup）：将模拟回报$G$反向传播到路径上的所有节点，更新其统计量。
  • $Q_i\leftarrow Q_i+G$
  • $N_i\leftarrow N_i+1$

在一定的迭代次数后，MCTS将根据累计回报的平均值返回最优动作。

像这种通过引入启发式函数指导搜索方向，显著减少计算量的优化搜索方法被称为启发式搜索。在MCTS中，启发式函数为UCB，而在优先遍历中，启发式函数为贝尔曼误差。包括异步DP、Dyna-Q+也以启发式搜索为核心思想。决策时规划由于对实时性的高要求，广泛应用了启发式搜索来大幅减少搜索空间，提升计算效率。