四边形不等式优化
应用于类似以下dp转移方程。
f i = min 1 ≤ j ≤ i ( w i , j , f i ) f_{i}=\min_{1\le j\le i}(w_{i,j},f_{i}) fi=1≤j≤imin(wi,j,fi)
假设 w i , j w_{i,j} wi,j 可以在 O ( 1 ) O(1) O(1) 的时间内进行计算。
在正常情况下,此状态转移方程的时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
对于问题 i i i,我们需要考虑所有的有关决策 j j j,但是当其满足决策单调性时,就可以缩小决策空间,减少时间复杂度。
四边形不等式:
约定:
对于类似 a ≤ b ≤ c ≤ d a\le b\le c\le d a≤b≤c≤d 都成立,若二元函数 w i , j w_{i,j} wi,j 满足以下条件
w a , c + w b , d ≤ w a , d + w b , c w_{a,c}+w_{b,d}\le w_{a,d}+w_{b,c} wa,c+wb,d≤wa,d+wb,c
则称 w i , j w_{i,j} wi,j 满足四边形不等式。
特别的,若等号永远成立,则称 w i , j w_{i,j} wi,j 为四边形恒等式。
重点:因为四边形不等式是用来优化时间复杂度的,所以四边形不等式给出了一个决策单调性的充分不必要条件。
利用决策单调性,可以使用二分查找,使其查询时间复杂度降低为 O ( N log N ) O(N \log N) O(NlogN)。
区间包含单调性
若 w b , c ≤ w a , d w_{b,c}\le w_{a,d} wb,c≤wa,d,则称 w w w 满足区间包含单调性。
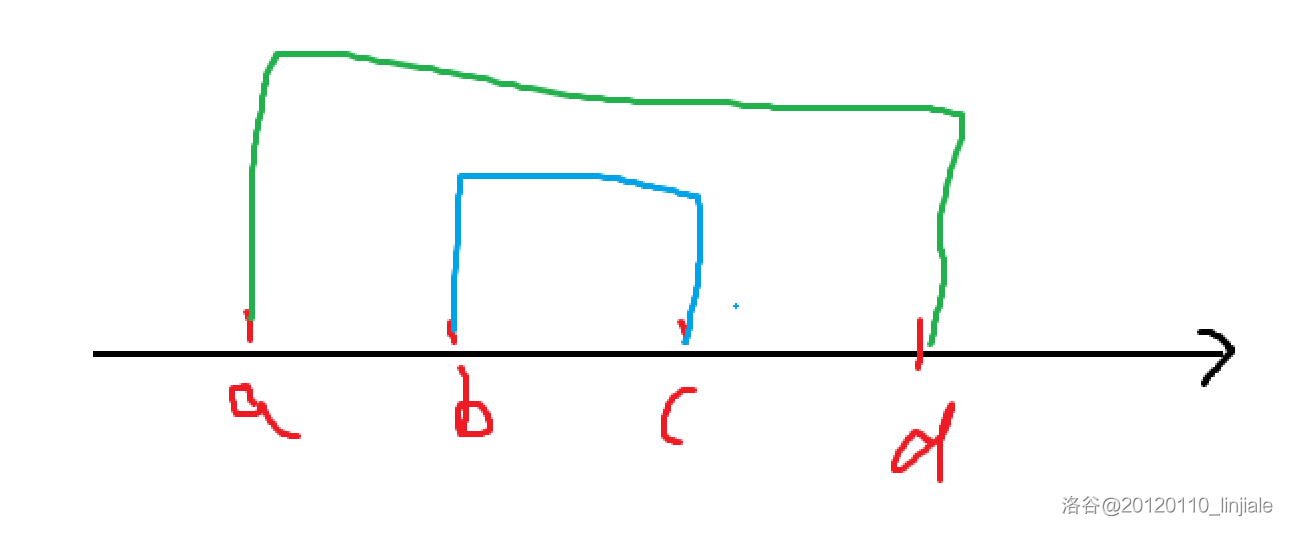
- 既包含,又满足决策单调性。
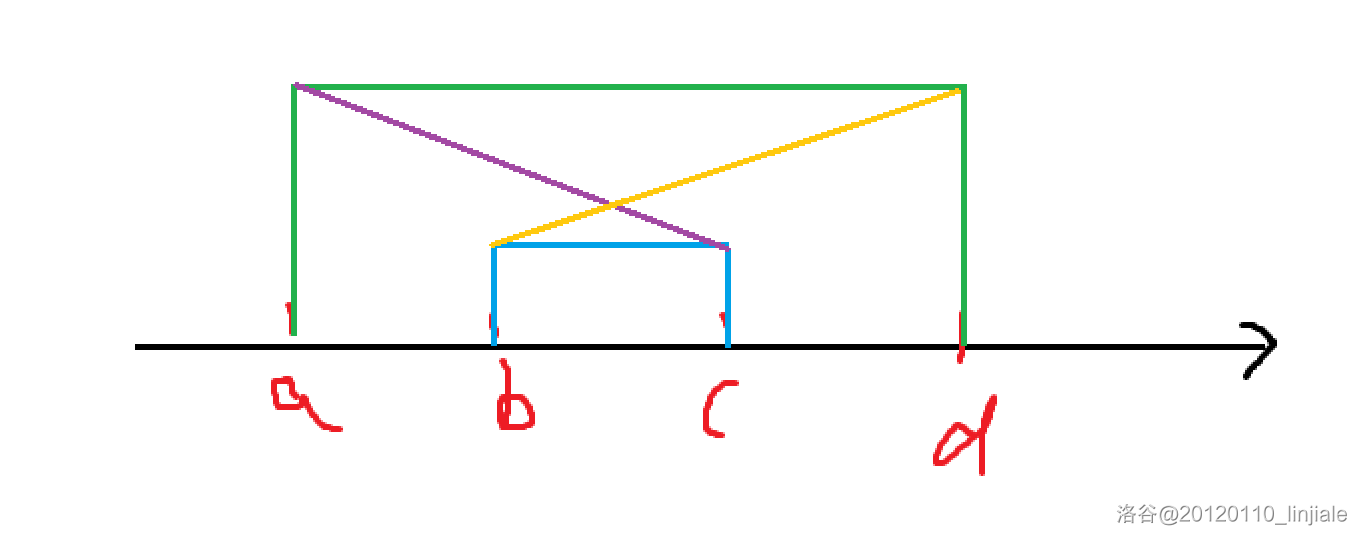
- 满足四边形不等式的形象化图片。
方程:
$$
w_{l,r+1}-w_{l,r}=a_{r+1}-a_{\lfloor\frac{l+r+1}{2}\rfloor}
\
w_{l+1,r+1}-w_{l+1,r}=a_{r+1}-a_{\lfloor\frac{l+r+2}{2}\rfloor}
\
$$


)
感知机)


